Stabwerk (Technische Mechanik)
In der Technischen Mechanik wird mit dem Begriff Stabwerk oder Stabtragwerk ein ebenes oder räumliches Tragwerk bezeichnet, das aus mehreren, miteinander verbundenen schlanken Stäben besteht. Die Stab-Verbindungen untereinander werden als Knoten bezeichnet. An speziellen Knoten – den Lager-Stellen – ist das Stabwerk mit der Umgebung verbunden. Das „Gegenteil“ zu den Stabtragwerken sind die Flächentragwerke, die beide zusammen die Tragwerke ausmachen.
Wenn das Stabwerk als Gesamtes längliche Form hat, werden die Längsseiten als Gurte, die begrenzenden Stäbe als Gurt-Stäbe bezeichnet.
Stäbe
In der Regel werden gerade Stäbe oder Balken verwendet. Ein Stabwerk, dessen Stäbe nur auf Druck oder Zug (Längs- oder Normalkraft), also nicht durch Querkraft und Biegemoment beansprucht werden, nennt man in der Fachsprache Fachwerk. Biegebeanspruchte Stäbe (Balken) werden üblicherweise breiter dimensioniert als die schlanken Stäbe eines idealen Fachwerks.
Knoten
Die Kraftkomponenten werden über die Knoten von Stab zu Stab geleitet. Die Stäbe können biegesteif oder biegeweich untereinander verbunden sein.[1] Biegesteife Ecken übertragen Biegemomente zwischen den verbundenen Balken.
Man spricht von fester Verbindung oder festem Anschluss (ecksteif), von Längs- oder Querkraftmechanismus (Längs- oder Querkraft-“Gelenk”[2]) und von (quasi)“gelenkiger” Verbindung oder “Gelenk” (eckweich). Bei einem ebenen Stabwerk können in diesen Verbindungen Normal- und Querkraft sowie Drehmoment (fester Anschluss), Querkraft und Drehmoment (Längsmechanismus oder Längskraft-“Gelenk”), Längskraft und Drehmoment (Quermechanismus oder Querkraft-“Gelenk”) oder Normal- und Querkraft (“Gelenk”) übertragen werden.
Lager
An den Lager-Stellen werden Kraftkomponenten (Kräfte und Drehmomente) aus dem Stabwerk heraus in die Umgebung übertragen. Je nach der Zahl der übertragenen Kraftkomponenten wird ein Lager als einwertig, zweiwertig, ... (bis n-wertig: n=3 bei ebenem, n=6 bei räumlichen Stabwerk) gekennzeichnet.[3] Beim ebenen Tragwerk ist ein unverschiebliches Drehlager zweiwertig, ein in der Tragwerksrichtung verschiebliches Drehlager (Loslager) einwertig und eine feste (unverschiebliche) Einspannung dreiwertig.
Fachwerk
In einem (idealen) Fachwerk werden die Stäbe nur von Normalkräften beansprucht. Bei realen Fachwerken treten im Allgemeinen auch geringfügige Biegemomente auf. Dadurch entstehen sog. Nebenspannungen. In statischen Berechnungen können bei der Vordimensionierung die Verbindungen wie (reibungsfreie) Drehgelenke behandelt werden.
Statische Bestimmtheit
Ein statisch unterbestimmtes („kinematisches“) Stabwerk wäre auf seinen Fundamenten oder in sich selber beweglich, also instabil. Statisch überbestimmte Stabwerke (= statisch unbestimmte Stabwerke) sind in der Regel stabiler als statisch bestimmte Stabwerke. Statisch unbestimmte Systeme können nicht mit den Gleichgewichtsbedingungen allein eindeutig gelöst werden, man braucht zusätzlich Verformungsrandbedingungen. Thermische Ausdehnungen und Setzungen der Fundamente können bei ihnen sekundäre, innere Beanspruchungen und Verformungen bewirken (also zusätzlich zu den von außen anliegenden Lasten wie Bauteilgewichten, Schnee- und Verkehrslast sowie Winddruck). Fertigungsungenauigkeiten bei den Stablängen können die Montage erschweren und auch zu sekundären, inneren Beanspruchungen und Verformungen führen (Zwängungen).
Aus den Gleichgewichtsbedingungen wurden für Stabwerke und nochmals speziell für Fachwerke die sogenannten Abzählkriterien als vereinfachte Bestimmungsmethode entwickelt. Für Grenzfälle liefern sie aber nicht immer das richtige Ergebnis, was wegen ihrer schematischen Anwendung zudem nicht erkennbar ist.
Erfahrene Stabwerk-Konstrukteure benutzen deshalb andere Kriterien wie das Abbau- bzw. Aufbaukriterien (Frage: Was passiert, wenn ein Stab entfernt bzw. ein Stab hinzugefügt wird?). Die sichere Antwort für jeden Fall und für Ungeübte folgt nur aus der Arbeit mit den Gleichgewichtsbedingungen.
Grad der statischen Bestimmtheit
Der Grad der statischen Bestimmtheit eines Stabwerks wird mit der ganzzahligen Größe angegeben:
- statisch überbestimmt / unbestimmt,
- oftmals statisch bestimmt,
- statisch unterbestimmt (=„kinematisch“ also beweglich).
Allgemeines Abzählkriterium
Die Bestimmung von n kann mit der folgenden, als Abzählkriterium bekannten Formel erfolgen:[Anm. 1][4]
- ebene Tragwerke:
- räumliche Tragwerke:
Hierbei sind:
i: Summe der in den Auflagern unterbundenen Bewegungsmöglichkeiten (Wertigkeiten der Auflager,)
j: Summe der in den Verbindungen unterbundenen Bewegungsmöglichkeiten (Wertigkeiten der Verbindungen),
k: Anzahl der starren Bauteile (deformierbare Stäbe zählen hier im Allgemeinen als starr (Ausnahme: zum Beispiel Fließgelenke)).
Rechenbeispiel: (ebener) Gerberträger
- ⇐ der Gerberträger ist ein statisch bestimmtes Tragwerk.
Mit dem Abzählkriterium ermittelte statische Unbestimmtheit entspricht immer der Realität, aber nicht immer ermittelte statische Bestimmtheit. Unter- und Überbestimmtheiten können sich bei diesem Verfahren gegenseitig aufheben. Beispiel hierfür ist ein zweiteiliger Balken, der auf drei Loslagern liegt: Trotz ermitteltem n = 0 ist er offensichtlich nicht statisch bestimmt.[Anm. 2]
Abzählkriterium für Fachwerke
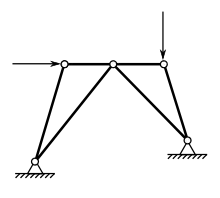
z = 5, a = 4, s = 6
Für Fachwerke kann man das allgemeine Abzählkriterium verwenden, da die Stäbe nur durch Normalkräfte belastet und alle Verbindungen als Drehgelenke bewertbar sind kann man sie vereinfachen:
Für ebene Fachwerke wird folgende Formel verwendet:[5][Anm. 3]
Hierbei sind:
a: Summe der in den Auflagerdrehgelenken unterbundenen Bewegungsmöglichkeiten (Wertigkeiten der Auflager),
s: Anzahl der Stäbe,
z: Anzahl der Drehgelenke (Auflager + Verbindungen).
Beispiel: nebenstehend abgebildetes Fachwerk
- ⇐ das nebenstehend abgebildete Fachwerk ist statisch bestimmt.
Für räumliche Fachwerke wird folgende Formel verwendet:[5][Anm. 3]
Die Abzählkriterien für Fachwerke sind nur eine notwendige, aber nicht hinreichende Bedingung für den Nachweis statischer Bestimmtheit.[Anm. 5]
Literatur
- Klaus-Jürgen Schneider, Erwin Schweda: Statisch bestimmte ebene Stabwerke. 2 Bde. 3., neubearb. Aufl., Werner, Düsseldorf 1985, ISBN 3-8041-3377-0 und ISBN 3-8041-3378-9.
- Walter Wunderlich, Gunter Kiener: Statik der Stabtragwerke. Teubner, Stuttgart 2004, ISBN 3-519-05061-7.
- Konstantin Meskouris, Erwin Hake: Statik der Stabtragwerke : Einführung in die Tragwerkslehre. 2. Aufl., Springer, Berlin 2009, ISBN 978-3-540-88992-2.
- Karl-Eugen Kurrer: Geschichte der Baustatik. Auf der Suche nach dem Gleichgewicht, Ernst und Sohn, Berlin 2016, ISBN 978-3-433-03134-6.
Einzelnachweise
- K. Meskouris, E. Hake: Statik der Stabtragwerke, Springer, 2009, S. 39
- Pichler, Bernhard. Eberhardsteiner, Josef: Baustatik VO LVA-Nr 202.065. TU Verlag (Memento des Originals vom 13. März 2016 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis. Wien, 2016 ISBN 9783903024175
- K. Meskouris, E. Hake: Statik der Stabtragwerke, Springer, 2009, S. 40
- Oliver Romberg, Nikolaus Hinrichs: Keine Panik vor Mechanik. Vieweg & Teubner Verlag, Wiesbaden 2011, ISBN 978-3-8348-1489-0, S. 35.
- Das „Föpplsche Gesetz“, vgl. Max Mengeringshausen: Raumfachwerke, Bauverlag GmbH, 1975, S. 28.
Anmerkungen
- Roman Harcke: Statische Bestimmtheit Abzählkriterium
- B. Marussig: Kraftgrößenverfahren, Seite 6: Nachteile des Abzählkriteriums
- statik-lernen.de: Statische (Un-)Bestimmtheit Abzählkriterium
- Marussig: Kraftgrößenverfahren, Seite 4, Abzählkriterien für Fachwerke
- Marussig: Kraftgrößenverfahren, Seite 5, Beispiel d: Abzählkriterim nicht hinreichend