Schwellenwert (Entwicklung)
Ein Schwellenwert wird definiert als Niveau, z. B. einer Genexpression oder eines Enzyms, ab dem sich ein Zielprodukt, z. B. ein Protein, Zellstatus oder ein anderes Phänotypmerkmal, nicht mehr linear verhält und sich ein Phasenwechsel vollzieht,[1] wobei eine Diskontinuität der sichtbaren Expression hervorgerufen wird. Schwellenwertverhalten ist ein weit verbreitetes Phänomen auf allen Ebenen der embryonalen Entwicklung (Ontogenese).[2][3][4]


Beispiele
Generell hat man bei einem Schwellenwert in der Regel eine unabhängige lineare, auf jeden Fall aber kontinuierliche Variable sowie eine abhängige nicht-lineare Variable, die den Schwellenwert ausbildet (Abb. 1). In einem einfachen Fall kann man sich die kontinuierliche Variable als abnehmende Konzentration einer Substanz vorstellen, in einem anderen Fall als linear zunehmende Genaktivierungsrate. Ein Beispiel für Schwellenwerte bei Farbmustern sind Farbübergänge auf Schmetterlingsflügeln (Abb. 2). Die Grenzen zwischen zwei Farben können mehr oder weniger scharf bzw. weich sein. Der Schwellenwertverlauf ist hier immer s-förmig (sigmoid); bei scharfer Farbtrennung zeigt die Übergangskurve einen steileren, bei sanfterem Farbübergang einen flacheren Verlauf. In jedem Fall ist der sigmoide Farbübergang nicht-linear bei linearem Verlauf des Genexpressionsniveaus.[4] Ein bekanntes Beispiel für das Vorhandensein eines Schwellenwertes in der Entwicklung ist die Wurfgröße. Die Anzahl von Jungen ist stets eine diskrete, diskontinuierliche Größe. Es wird angenommen, dass sie mit einer oder mehreren kontinuierlichen Variablen korreliert; hier ist es hauptsächlich die Aktivität gonadotroper Hormone, welche die Anzahl ovulierter Eier bestimmt, sowie weitere hormonelle Faktoren. Die Geschlechtsbestimmung einiger Schildkröten und anderer eierlegender Reptilien gehorcht bruttemperaturabhängigen Schwellenwerteffekten (Abb. 1). Die S-Übergangskurve ist in diesem Fall sehr abrupt, steil, da ja nur zwei Geschlechtsformen, männlich und weiblich, existieren. Auch die Bildung der Somiten in der Entwicklung wird schon lange mit Schwellenwerteffekten erklärt und simuliert, zuerst von Hans Meinhardt[6] und darauf aufbauend neuerdings auch mit konkreten Gennetzwerken empirisch untermauert[5] (Abb. 4). Ein weiteres Beispiel ist die Anfälligkeit für eine Krankheit, die sich ebenfalls nur diskret ausprägen kann (krank / nicht krank), während die molekularbiologischen Voraussetzungen hierfür nicht als diskret gesehen werden können. Man spricht daher von einer Kontinuität mit Schwellenwert.[7][8]
Entstehen und Eigenschaften
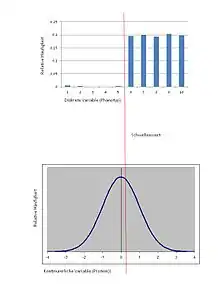
Fred Nijhout hat analysiert, dass stochastische Genexpressionen inhärent Schwellenwerte beinhalten.[4] Stochastik erzeugt nach dieser Sicht Schwellenwerte. Reaktions-Diffusionssysteme oder Aktivator-Inhibitor-Systeme nach Gierer-Meinhardt implizieren ebenfalls von ihrer mathematischen Logik her die Ausbildung von Schwellenwerten. Die Muster, die solche Modelle beschreiben sind an ihren Umgebungsgrenzen durch Schwellenwerte charakterisiert. Die Modelle beschreiben mathematisch, wie Schwellenwerte entstehen. Die Steilheit des Übergangs eines Schwellenwerts gibt der Hill-Koeffizient wieder. Bestimmend für den Verlauf können unterschiedliche Modellparameter sein, etwa Genaktivierung, Geninhibition, Diffusionskonstanten etc. oder exogene Faktoren. Die Projektion diskreter Werte in eine kontinuierliche Variable, von der häufig angenommen werden kann, dass sie normalverteilt oder annähernd normalverteilt ist,[9] erlaubt die Anwendung stochastischer Analysen der Quantitativen Genetik[7] (Abb. 3).
Ein Schwellenwert kann durch das Maß eines Umweltfaktors als kontinuierliche Variable bestimmt sein, z. B. Temperatur. Auch induzierte Hitzeschocks können Schwellenwerteffekte auslösen. Conrad Hal Waddington konnte erstmals zeigen, dass Hitzeschocks im Puppenstadium einer Population von Drosophila melanogaster zur Eliminierung der Querverstrebungen von Flügeladern (crossveinless) führen können,[10] was erst später genetisch assimiliert wird (genetische Assimilation).
Ferner kann ein Schwellenwert durch ein komplexes, interdependentes Zusammenspiel mehrerer Genprodukte bei der Genregulation bestimmt sein, wodurch das Niveau von Transkriptionsfaktoren bestimmt wird.[11] Ein Beispiel für komplexe Schwellenwertmechanismen ist die präaxiale Polydaktylie der Katze. In diesem Fall werden mehrere, molekularbiologisch nicht im Detail bekannte Schwellenwerte angenommen, etwa für die Ausbildung von 20, 22, 24 oder 26 Zehen eines Individuums (Wildtyp: 18 Zehen). Die Vererbung erfolgt nicht nach den einfachen mendelschen Regeln. Das wird verständlich, wenn man berücksichtigt, dass für den Polyphänismus der Zehenzahlen genetisch stets dieselbe Punktmutation zugrunde liegt.
Implikationen für Entwicklung und Evolution
Schwellenwerteffekte können mitbewirken, dass eine marginale genetische Änderung, etwa eine Punktmutation, zu einer umfangreichen phänotypischen Variation, quasi zu einem „Quantensprung“ führt. Oder auch: Eine lineare Genaktivierungsrate verursacht einen plötzlich hohen räumlichen Prozentsatz aktivierter Gene.[4] Beide Betrachtungen sind grundlegend für die evolutionäre Entwicklungsbiologie (Evo-Devo).[12] Bei Stephen Jay Gould heißt es dazu bereits 1980: „Wenn wir uns nicht auf diskontinuierliche Veränderungen durch geringfügige Abweichungen von der Entwicklungsgeschwindigkeit berufen, dann sehe ich in der Tat nicht, wie die meisten größeren evolutionären Übergänge überhaupt erklärt werden könnten.“[13] Heute diskutiert man in diesem Zusammenhang neben der Veränderung der Entwicklungsgeschwindigkeit (Heterochronie) auch die Parameter Ort (Heterotopie), Art des erzeugten Genprodukts (Heterotypie) sowie Vermehrung oder Verminderung des erzeugten Genprodukts (Heterometrie) als Ausgangsparameter, die Schwellenwerte auslösen können.[14]
Schwellenwertmechanismen führen zu robuster Entwicklung. Sie stellen Constraints dar. Kleine Expressionänderungen können ohne Wirkung bleiben; sie bleiben kanalisiert. Schwellenwerte können dann nicht unerwünscht überschritten werden. Man kann sagen, die Entwicklung ist in diesem Bereich insensitiv für die Variation. Wird ein Schwellenwert aber z. B. in der Folge einer Mutation oder eines Umweltfaktors überschritten, ist die Konsequenz (Dekanalisierung) wider Erwarten oft nicht chaotisch, sondern jetzt können zuvor verdeckte (kryptische), unter Umständen vielfach akkumulierte Variationen bzw. versteckte Entwicklungspfade offengelegt werden, und es kann im Rahmen der integrativen Leistungen der Entwicklung evolutionär zu einer beachtlichen phänotypischen Variation oder Innovation kommen, über deren Durchsetzung und Bestand in der Population die natürliche Selektion final bestimmen kann.[15]
Mit der Einführung von Schwellenwerteffekten erweitert die Evolutionstheorie sowohl die Argumentation Darwins wie auch die der Synthetischen Evolutionstheorie, wonach Variationen stets graduell in kleinsten Schritten und damit über evolutionär lange Zeitstrecken verlaufen (Gradualismus). Variation wird heute vor allem von der Evolutionären Entwicklungsbiologie nicht mehr ausschließlich gradualistisch gesehen (Altenberg-16).
Einzelnachweise
- A. Lange: Darwins Erbe im Umbau. Königshausen & Neumann, 2012, ISBN 978-3-8260-4813-5, S. 383.
- Gerd B. Müller: Epigenetic Innovation. In: Massimo Pigliucci, Gerd B. Müller: Evolution. The Extended Synthesis. MIT Press, 2010, ISBN 978-0-262-51367-8, S. 316f.
- Scott F. Gilbert, David Epel: Ecological Developmental Biology. Sinauer, 2009, ISBN 978-0-87893-299-3, S. 380.
- H. F. Nijhout: Stochastic Gene Expression: Dominance, Thresholds and Boundaries. In: Reiner A. Veita (Hrsg.): The Biologiy of Genetic Dominance. Eurekah.com, 2004, Chapter 8.
- H. B. Tiedemann, E. Schneltzer, S. Zeiser, B. Hoesel, J. Beckers u. a.: From Dynamic Expression Patterns to Boundary Formation in the Presomitic Mesoderm. In: PLoS Comput Biol. Band 8, Nr. 6, 2012, S. e1002586. doi:10.1371/journal.pcbi.1002586.
- Hans Meinhardt: Models of Biological Pattern Formation. Academic Press, London 1982, ISBN 0-12-488620-5.
- Douglas S. Falconer: Einführung in die Quantitative Genetik. Ulmer, Stuttgart 1984, ISBN 3-8001-2532-3, Kap. 18.
- Jingjing Li: The Evolutionary Implication of Gene Expression Variation in Eukaryotes: From Yeast to Human. Dissertation. 2011, ISBN 978-0-494-78260-6, S. 80ff.
- Jingjing Li: The Evolutionary Implication of Gene Expression Variation in Eukaryotes: From Yeast to Human. Dissertation. 2011, S. 6ff.
- C. H. Waddington: Genetic Assimilation of an Acquired Character. In: Evolution. Band 7, 1953, S. 118–126.
- Gerd B Müller: Epigenetic Innovation. In: Massimo Pigliucci, Gerd B. Müller: Evolution. The Extended Synthesis. MIT Press, 2010, S. 317.
- Gerd B. Müller: Epigenetic Innovation. In: Massimo Pigliucci, Gerd B. Müller: Evolution. The Extended Synthesis. MIT Press, 2010, S. 307–332.
- Stephen J. Gould: Der Daumen des Panda – Betrachtungen zur Naturgeschichte. Suhrkamp Taschenbuch Wissenschaft, 1989, ISBN 3-518-28389-8, S. 302.
- Wallace Arthur: Biased Embryos and Evolution. Cambridge University Press, 2004, ISBN 0-511-21180-5, S. 81.
- Gerd B. Müller: Epigenetic Innovation. In: Massimo Pigliucci, Gerd B. Müller: Evolution. The Extended Synthesis. MIT Press, 2010, S. 316ff.