Schartenhöhe
Die Schartenhöhe oder Prominenz, auch Schartentiefe oder relative Einsattelung genannt, ist ein Maß für die Selbständigkeit eines Gipfels, Bergs oder einer anderen geomorphologischen Landform. Neben der Dominanz ist sie ein wichtiges Kriterium, um einen Berg als solchen zu klassifizieren. Bei einer wenig ausgeprägten Erhebung, etwa auf einem Grat oder Plateau, ist die Schartenhöhe vergleichsweise gering, und man spricht dann von einem Nebengipfel oder einer Graterhebung.[1]
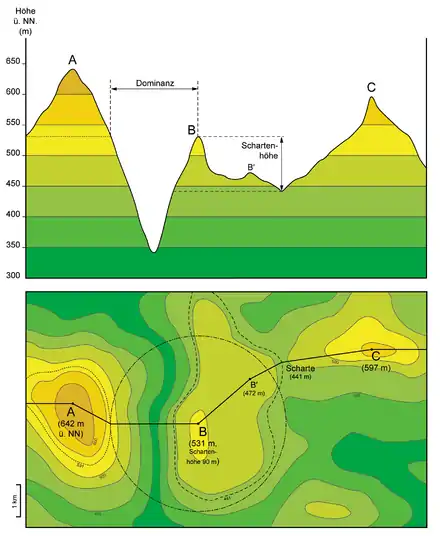
Definitionen
- Die Schartenhöhe eines Gipfels ergibt sich als Differenz aus seiner Höhe und der höchstgelegenen Einschartung (Bezugsscharte, englisch: key col)[2], bis zu der man mindestens absteigen muss, um einen höheren Gipfel zu erreichen.[3]
- Die Schartenhöhe eines Gipfels ist seine Höhe über der niedrigsten geschlossenen Höhenlinie, die ihn umgibt und gleichzeitig keinen höheren Gipfel einschließt.
Die beiden Definitionen sind gleichbedeutend, wenn man davon absieht, dass auf den höchsten Berg der Erde die erste nicht angewendet werden kann, da kein höherer Gipfel existiert.
Der Begriff der relativen Einsattelung wurde von Klaus Hormann 1965 präsentiert.[4]
Gedankenexperiment zur Veranschaulichung
Lässt man den Meeresspiegel so lange ansteigen, bis auch die letzte Landverbindung zwischen Berg X und einer beliebigen höheren Landstelle überflutet wird, Berg X also den höchsten Punkt einer Insel zu bilden beginnt, dann ist die zuletzt überflutete Geländebrücke die Bezugsscharte von Berg X, und die Höhendifferenz zwischen der Scharte (oder dem gestiegenen Meeresspiegel) und seinem Gipfel ist seine Schartenhöhe.
Begriffe und Konventionen
- Bildet ein Berg den höchsten Gipfel einer Landmasse, dann ist seine Schartenhöhe gleich seiner Höhe über dem Meer. Das Meer wird also auch als mögliche Scharte betrachtet.
- Die Schartenhöhe des höchsten Berges der Erde, des Mount Everest, entspricht gemäß der zweiten gegebenen Definition ebenfalls seiner Höhe über dem Meer.
- Unter der Annahme, dass keine zwei Scharten exakt gleich hoch sind, existiert für jeden Berg genau eine Bezugsscharte. Umgekehrt kann jede Scharte nur für einen bestimmten Berg als Bezugsscharte gelten, wenn man davon ausgeht, dass sich Grate nicht an Scharten verzweigen.
- Ein normierter (skalierter) abgeleiteter Wert ist die Orographische Dominanz, die die Schartenhöhe ins Verhältnis zur Höhe setzt.
Bezugsberge
Sieht man vom Mount Everest ab, kann man für jeden Gipfel jenseits der maßgeblichen Scharte (einschließlich des Meeresspiegels) zu mindestens einem höheren Berg gelangen. Einige dieser Berge mit gewissen Eigenschaften werden verschiedentlich als spezielle Bezugsberge für die Prominenz des betreffenden Gipfels gelistet. In der vorwiegend englischsprachigen Literatur werden sie als Parent Mountains bezeichnet. Einige gängige Konzepte werden im Folgenden vorgestellt.
Line Parent
Der Line Parent eines Gipfels ist der jenseits der Bezugsscharte dem Kammverlauf folgend nächstliegende höhere Gipfel, den man erreichen kann, ohne tiefer absteigen zu müssen. Da der Line Parent selbst eine gewisse Selbständigkeit aufweisen soll, muss für ihn eine Mindest-Schartenhöhe festgesetzt werden (vgl. Selbständigkeit von Bergen und Gipfeln im Hochgebirge). Je nachdem, welchen Wert man hier ansetzt, kann man zu unterschiedlichen Line Parents für denselben Gipfel gelangen.[5] Darüber hinaus wurden verschiedene Ansätze verfolgt, wie der Line Parent zu ermitteln ist, wenn sich z. B. der Grat jenseits der Bezugsscharte teilt und man die Wahl zwischen zwei höheren Bezugsbergen hat. So hat Ron Tagliapietra vorgeschlagen, den – gemessen entlang des Gratverlaufs – nächstgelegenen höheren Gipfel als Bezugsberg heranzuziehen, auch wenn dieser der niedrigere der beiden Kandidaten ist.[6]
.png.webp)
.png.webp)
Prominence Master
Der Prominence Parent eines Gipfels, oft auch als Prominence Master bezeichnet, ist der dem Kammverlauf folgend nächstliegende prominentere Gipfel, den man über die Bezugsscharte erreichen kann, ohne tiefer absteigen zu müssen. Der Prominence Master ist stets auch höher als der Ausgangsgipfel. Da er immer eine größere Schartenhöhe als der Ausgangsgipfel besitzt, kann man hier von einer Abstammung im eigentlichen Sinne sprechen. Gleichzeitig wird die Festlegung einer Mindestschartenhöhe, wie sie bei der Line Parentage erforderlich ist, vermieden. Für jeden Gipfel lässt sich damit eine Reihe immer höherer und prominenterer Berge ermitteln, die mit dem Gipfel beginnt und beim höchsten Berg der jeweiligen Landmasse (Insel oder Kontinent) endet.[7]
Dennoch ist auch der Prominence Master damit nicht in jedem Fall, etwa bei Gratverzweigungen hinter der Bezugsscharte, eindeutig bestimmt. Der Engländer Peter Ridges hat daher eine Entscheidungsregelung formuliert, nach der als Parent derjenige Gipfel gilt, dessen niedrigster Punkt im Kammverlauf nach der Gratverzweigung höher liegt als der niedrigste Punkt auf dem Verbindungskamm eines weiteren Kandidaten (»higher lowest point property«)[8].


Island Parent
Vergleichbar zur obigen Definition der Schartenhöhe kann man sich vorstellen, dass der Meeresspiegel soweit steigt, bis die letzte Verbindung zu einem höheren Berg als Landzunge gerade noch aus dem Wasser ragt. Somit ist der Gipfel mit einer weiteren Landmasse zu einer einzigen Insel verbunden, deren höchste Erhebung als Island Parent oder Encirclement Parent bezeichnet wird. Abgesehen von einigen Spezialfällen, etwa Kratern mit Zentralbergen, kann man sich den Island Parent als höchsten Gipfel vorstellen, der ausgehend von der jeweiligen Bezugsscharte über einen in jedem Punkt ansteigenden Weg erreicht werden kann. Er ist damit auch der nächsthöhere Berg, dessen eigene Bezugsscharte niedriger liegt als die des betrachteten Berges. Anders als Line Parent und Prominence Master ist der Island Parent von vornherein eindeutig bestimmt. Wie bei der Prominence Parentage lässt sich für jeden Gipfel eine eindeutige »Abstammungslinie« mit prominenteren Island Parents ermitteln.[9]
Während jeder Berg genau eine Bezugsscharte hat und jede Scharte Bezugsscharte für genau einen Berg ist, können mehrere Berge den gleichen Parent Mountain haben.
Beispiele
- Um vom höchsten Berg Österreichs aus, dem 3798 m ü. A. hohen Großglockner, einen höheren Berg zu erreichen, muss man mindestens bis zum Brennerpass (1370 m ü. A.) absteigen. Aus den zugehörigen Höhenangaben ergibt sich als Differenz eine Schartenhöhe von 2428 m. Damit ist der Großglockner der zweitprominenteste Berg der Alpen.[10] Der in einem möglichen Kammverlauf folgende nächste höhere Berg, den man über den Brennerpass erreichen kann, ohne tiefer absteigen zu müssen (Line Parent), ist der 3905 Meter hohe Ortler in Südtirol, der mit 1953 Metern eine geringere Schartenhöhe aufweist als der Großglockner selbst. Nächsthöherer geografischer Nachbar des Großglockners in Luftlinie (Dominanz) ist die dem Ortler benachbarte 3851 Meter hohe Königspitze, die vom Brennerpass aus gesehen im Kammverlauf jedoch hinter dem Ortler liegt. Der Prominence Master und Island Parent des Großglockners ist der Mont Blanc, der mit 4810 Metern der höchste Alpengipfel ist.
- Der zweithöchste Berg Österreichs, die 3768 m ü. A. hohe Wildspitze in Tirol, steht dem Großglockner an Höhe kaum nach. Sie teilt mit diesem zwar den Island Parent (Mont Blanc), ihr Prominence Master ist jedoch das Finsteraarhorn (4274 m ü. M.) in den Berner Alpen, zu dem man über den als Bezugsscharte fungierenden 1507 m s.l.m. hohen Reschenpass gelangt. Die Prominenz des Finsteraarhorns liegt mit 2279 m gerade zwischen der des Glockners (2428 m) und der der Wildspitze (2261 m). Der Prominenzsattel des Finsteraarhorns liegt in einer Höhe von 1995 m ü. M. beim Simplonpass. Mont Blanc, Großglockner, Finsteraarhorn und Wildspitze sind die vier prominentesten Berge der Alpen.[10]
- Der Prominence Master und Island Parent des Mont Blanc ist der höchste Berg der Erde, der 8848 m hohe Mount Everest im Himalaya. Die geografisch nächsten höheren Berge befinden sich dagegen im viel näher liegenden Kaukasus. Der dem Elbrus (5642 m) naheliegende Kjukjurtlju (4912 m) ist Dominanz-Referenzberg für den Mont Blanc.
- Beispiel für die Unterscheidungsregel nach Peter Ridges: Die Zugspitze hat als Bezugsscharte den Fernpass. Der Kamm jenseits der Bezugsscharte verläuft nördlich des Inns nach Westen zu einem möglichen Prominence Parent. Nördlich der Innquelle verzweigt sich der Kamm zu den Kandidaten Finsteraarhorn und Piz Bernina – beide sind höher und prominenter als die Zugspitze. Der Piz Bernina liegt im Kammverlauf zwar wesentlich näher, der Kamm von der Verzweigung zum Piz Bernina hat jedoch im 1815 Meter hohen Malojapass seinen niedrigsten Punkt. Diese Höhe muss auf dem Kamm von der Verzweigung zum Finsteraarhorn nicht mehr unterschritten werden, sodass das Finsteraarhorn als Prominence Parent der Zugspitze bestimmt werden kann.
- Um vom Großen Hundstod (2593 m) in den Berchtesgadener Alpen zu einem höheren Gipfel zu gelangen, muss man mindestens bis zur Dießbachscharte (2119 m) absteigen, über die man z. B. zur Schönfeldspitze (2653 m) oder zum Selbhorn (2655 m) im Steinernen Meer gelangen kann. Damit ergibt sich hier eine Schartenhöhe von 474 Metern. Hier ist auch ersichtlich, dass die Schartenhöhe nicht zwingendermaßen der Höhe eines Gipfels über derjenigen Scharte entspricht, die zum nächstgelegenen höheren Berg führt. Denn der nächstgelegene höhere Berg ist in diesem Fall der Watzmann (2713 m), allerdings muss man, um zu diesem zu gelangen, bis zum 1774 Meter hoch gelegenen Trischübelpass noch weiter absteigen. Der Prominence Master und gleichzeitig Island Parent für den Großen Hundstod ist der Hochkönig, der als höchster Berg der Berchtesgadener Alpen die größte Schartenhöhe in den Nördlichen Kalkalpen aufweist und damit auch zu den prominentesten Gipfeln im gesamten Alpenraum[10] zählt.
Selbständigkeit von Gebirgsgruppen, Bergen und Gipfeln
| Berge | 150 m |
| Berggruppen | 500 m |
| Hauptgruppen | 1000 m |
| Großgruppen | 2000 m |
Gebirgssystematiken
Hormann[4] hat zur geomorphometrischen Klassifikation von Gebirgsgruppen das Maß der relativen Einsattelung entwickelt (vgl. Tabelle). Im Unterschied zu Bergen sind die eingangs genannten Definitionen nicht gleich, weil eine Gebirgsgruppe nicht von einer geschlossenen Höhenlinie umgeben sein muss (bzw. einer, die keinen höheren Gipfel enthält): Hier ist die Prominenz der Gruppe aber immer die Schartenhöhe ihres höchsten Berges über der höchsten Scharte ihrer Umgrenzungslinie.
Tatsächlich haben sich solche Systeme im Alpinismus nicht durchgesetzt, weil die Gruppen – außer metrisch präzise bestimmt zu sein – kaum Vorteile haben. Insbesondere sind die so erzielten Gliederungen wenig flächengleich: So findet sich in den Alpen unter den zehn Bergen mit höchster Schartenhöhe mit dem Hochkönig (Gruppe Berchtesgadener Alpen und Dientener Berge) eine im Vergleich zu den anderen Dominanzgruppen sehr kleine Gruppe, und unter den 13 Bergen mit Schartenhöhen von mehr als 2000 m mit dem Säntis (Alpsteingebiet) eine weitere.
Hochgebirge
In den Alpen gilt nach einer von der UIAA getroffenen Festlegung eine Erhebung als Gipfel, wenn ihre Schartenhöhe mindestens 30 Meter beträgt.[12] Um bei einem Gipfel auch von einem eigenständigen Berg zu sprechen, werden für die Alpen ein Mindestmaß von ca. 100[13] bis 300[14] Metern Schartenhöhe genannt. Im Himalaya sind sogar 500[15] Meter als Wert zu finden.
Für die weltweit gut 1500 Berge mit einer Schartenhöhe von mehr als 1500 Metern (davon liegen 44 in den Alpen) findet sich in der englischen Literatur die Bezeichnung Ultra Prominent Peak.[14][16]
Über die objektiven Kriterien wie Dominanz und Schartenhöhe hinaus sind jedoch in der Praxis auch subjektive Faktoren für die Bezeichnung als Berg bestimmend. So können etwa die alpinistische Bedeutung, die Aussicht vom Gipfel, die optische Dominanz vom Tal aus oder der Eintrag auf einer Landkarte entscheidend dafür sein, dass eine Erhebung als Berg bezeichnet wird. Es gibt also sowohl bekannte und alpinistisch bedeutende Gipfelpunkte mit sehr niedrigen Schartenhöhen als auch umgekehrt Berge, die trotz hoher Eigenständigkeit nicht einmal benannt sind.[13]
Mittelgebirge
Auch im Mittelgebirge wird die Schartenhöhe zur Bestimmung der Eigenständigkeit von Bergen herangezogen. Dies macht eine Anpassung der Zahlen erforderlich, da die Höhenunterschiede dort geringer sind als im Hochgebirge und Schartenhöhen von 300 m höchst selten sind. Für die Eigenständigkeit von Gipfeln werden dabei je nach Höhenlage Mindestschartenhöhen von 11 bis 14 Metern verwendet.[17] Allerdings fehlen bislang verbindliche Werte, die alle für Mittelgebirge relevanten Höhenlagen erfassen und allgemein anerkannt sind. Die Festlegung einheitlicher Werte für die Mindestschartenhöhe eigenständiger Mittelgebirgsgipfel wird durch den Umstand erschwert, dass die Berge hier traditionell über deren subjektives Erscheinungsbild definiert werden und gemeinhin keine Notwendigkeit gesehen wird, über die Schartenhöhe eine Neudefinition vorzunehmen. Nicht zuletzt deshalb ist der Begriff Schartenhöhe in Literatur und allgemeinem Bewusstsein in Bezug auf Mittelgebirge deutlich weniger etabliert als im Hinblick auf Hochgebirge.
Literatur
Theorie:
- Peter Grimm, Claus Roderich Mattmüller (Hrsg.): Die Gebirgsgruppen der Alpen. Ansichten, Systematiken und Methoden zur Einteilung der Alpen (= Wissenschaftliche Alpenvereinshefte. H. 39). Deutscher Alpenvereinsverlag, München 2004, ISBN 3-937530-06-1 (mit zahlreichen Beiträgen zur Methodologie).
- Claus Roderich Mattmüller: Zur orographischen Gliederung von Gebirgen. In: Zeitschrift für Geomorphologie. Bd. 55, Nr. 1, 2011, ISSN 0372-8854, S. 109–140, doi:10.1127/0372-8854/2011/0055-0038.
Zu Bergen:
- Adam Helman: The finest Peaks. Prominence and other Mountain Measures. Trafford Publishing, Victoria 2005, ISBN 1-4120-5994-1 (eingeschränkte Vorschau in der Google-Buchsuche).
- Richard Goedeke: Top 20 der Alpen. Die wichtigsten Anstiege auf die prominentesten Berge. Bruckmann, München 2008, ISBN 978-3-7654-4851-5.
Weblinks
- Prominence Theory (englisch)
- Wolfgang Leonard: The high rise pages.de. Abgerufen am 5. Mai 2012.
Anmerkungen und Einzelnachweise
- Abweichend davon bezeichnet Schartenhöhe gelegentlich einfach die Höhe der Scharte über dem Meeresspiegel und ist dann von der Prominenz zu unterscheiden, vgl. etwa Eigenständigkeit von Gipfeln, thehighrisepages.de
- »Scharte« steht hier für den mathematischen Sattelpunkt, den Punkt einer Fläche mit waagrechter Tangentialebene und entgegengesetzten Krümmungen, also stellvertretend für alle geomorphologisch-landschaftlichen Formen der Gebirgspässe, Bergsättel, Joche etc.
- Christian Thöni: Wie berechnet man die Schartenhöhe eines Berges? www.gipfelverzeichnis.ch
- Klaus Hormann: Uber die morphographische Gliederung der Erdoberfläche. In: Mitteilungen der Geographischen Gesellschaft in München 50, 1965, S. 109–126 (Fundstelle S. o.A.); auch: ders.: Relative Einsattelung und Rampenlänge der Pässe von Kärnten und Osttirol. In: Mitt. d. Geogr. Ges. in München. München 1966.
- Der Line Parent wird zuweilen auch als Next oder Nearest Higher Neighbor (NHN) bezeichnet (vgl. z. B. Prominence Theory. Section 6: Lineage Theory. In: Peaklist.org. Abgerufen am 17. Oktober 2011 (englisch).). Andere Quellen benutzen die Bezeichnung NHN für den nach dem Dominanz-Prinzip tatsächlich nächstgelegenen höheren Berg, vgl. z. B. Peakbagger. Help and Glossary. In: Peakbagger.com. Abgerufen am 17. Oktober 2011 (englisch).
- Vgl. z. B. Adam Helman: The Finest Peaks. Prominence and other Mountain Measures. Trafford Publishing, 2005, ISBN 1-4120-5995-X, S. 83 ff. (eingeschränkte Vorschau in der Google-Buchsuche).
- Lässt man den Meeresspiegel als Bezugsscharte zu, endet die Reihe zuletzt beim Mount Everest.
- Siehe Adam Helman: The Finest Peaks. Prominence and other Mountain Measures. Trafford Publishing, 2005, ISBN 1-4120-5995-X, S. 85 (eingeschränkte Vorschau in der Google-Buchsuche).
- Prominence Theory. Section 6: Lineage Theory. Peaklist.org, abgerufen am 17. Oktober 2011 (englisch).
- Liste der prominentesten Berge der Alpen
- Zitiert nach Stefan Rasemann: Geomorphometrische Struktur eines mesoskaligen alpinen Geosystems. Dissertation Rheinische Friedrich–Wilhelms–Universität Bonn. Bonn 2003, 2.1.2 Definition und Abgrenzung des Hochgebirges: Geomorphometrische Unterteilung von Hochgebirgssystemen – Tabelle 2.4: Größenordnungen der Berggruppierung auf Basis der relativen Einsattelung zur semi–quantitativen Unterteilung von Hochgebirgssystemen (Hormann, 1965), S. 41, urn:nbn:de:hbz:5n-02113.
- UIAA Dokumentations- und Informationskommission: Die Viertausender der Alpen – Offizielles UIAA-Verzeichnis. In: UIAA-Bulletin. Nr. 145, März 1994, S. 9 f. (online [PDF; 630 kB; abgerufen am 15. Mai 2008]).
- Christian Thöni: Von Schartenhöhe und Dominanz. In: Die Alpen. Nr. 1/2003, Januar 2003 (PDF, 0,2MB (Memento vom 7. Juli 2011 im Internet Archive) [abgerufen am 3. Juli 2007]). Von Schartenhöhe und Dominanz (Memento des Originals vom 7. Juli 2011 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.
- Eberhard Jurgalski: Erläuterung Dominanzsystem. In: extreme-collect.de. Abgerufen am 16. Oktober 2011.
- thehighrisepages.de: Eigenständigkeit von Gipfeln.
- The World Ultras Homepage. In: Peaklist.org. Abgerufen am 17. Oktober 2011.
- Gipfel im Taunus, thehighrisepages.de