Satz von Ringel-Youngs

Der Satz von Ringel-Youngs, auch Heawood-Vermutung genannt, gibt in der Graphentheorie eine Formel für die minimale Anzahl der Farben, die für die Färbung einer beliebigen Fläche nötig ist abhängig vom topologischen Geschlecht der Fläche (wobei hier ein Geschlecht $g>0$ betrachtet wird).

Percy Heawood hatte die Formel 1890 angegeben, bewiesen, dass diese Formel für Geschlecht $g>0$ eine obere Schranke darstellt und die Vermutung formuliert, dass sie auch eine untere Schranke ist. Das heißt, er bewies, dass jede Landkarte auf den entsprechenden Flächen mit der durch die Formel angegebenen Anzahl von Farben färbbar ist, und vermutete, dass man im Allgemeinen nicht mit weniger Farben auskommt. 1968 wurde das von Gerhard Ringel und J. W. T. Youngs bewiesen, mit Ausnahme der Fälle der Kleinschen Flasche und der Kugel. Der Fall der Kugel (Geschlecht g=0) entspricht dem schwierigen Fall des Vier-Farben-Satzes (wobei hier das Problem darin liegt die obere Schranke zu beweisen, für die untere Schranke kann man eine einfache Landkarte angeben, die nur mit vier Farben färbbar ist[1]) und wurde erst 1977 bewiesen, die Formel ist aber auch hier gültig. Die Kleinsche Flasche blieb eine Ausnahme für die Gültigkeit der Formel.

Formale Darstellung

Der Franklin-Graph.

Percy Heawood vermutete 1890, dass für ein gegebenes Geschlecht g > 0 die minimale Anzahl der benötigten Farben für die Färbung aller Graphen auf der Oberfläche einer orientierbaren Mannigfaltigkeit dieses Geschlechts (oder äquivalent dazu die Färbung einer Zerlegung dieser Fläche in einfach zusammenhängende Flächen) gegeben ist durch:

\gamma (g)=\left\lfloor {\frac {7+{\sqrt {1+48g}}}{2}}\right\rfloor ,

wobei $\left\lfloor x\right\rfloor$ die Abrundungsfunktion ist.

Wenn man das Geschlecht durch die Euler-Charakteristik ersetzt, erhält man die Formel, die sowohl orientierbare als auch nicht-orientierbare Fälle abdeckt,

\gamma (\chi )=\left\lfloor {\frac {7+{\sqrt {49-24\chi }}}{2}}\right\rfloor .

Diese Formel funktioniert, wie Ringel und Youngs bewiesen, für alle Flächen, außer für die Kleinsche Flasche. Philip Franklin bewies 1930, dass für die Kleinsche Flasche höchstens 6 Farben benötigt werden, statt 7 wie von der Formel vorhergesagt. Der Franklin-Graph kann in eine Kleinschen Flasche gezeichnet werden, so dass sie sechs sich gegenseitig berührende Flächen bildet. Somit ist diese Grenze scharf.

In der einen Richtung ist der Beweis unkompliziert: Durch Manipulation der Euler-Charakteristik kann man zeigen, dass jeder Graph, der in die Oberfläche eingebettet ist, wenigstens einen Knoten des Grades kleiner als die gegebene Schranke hat. Wenn man diesen Knoten entfernt und den restlichen Graphen färbt, dann gewährleistet die kleine Anzahl von Nachbarknoten, dass man den entfernten Knoten dem Graphen wieder hinzufügen kann, ohne die Farbanzahl wieder zu erhöhen. In umgekehrter Richtung ist der Beweis komplizierter und erfordert, dass in jedem Fall (außer der Kleinschen Flasche) ein Vollständiger Graph mit der Anzahl von Knoten gleich der Anzahl der Farben auf der Oberfläche gezeichnet werden kann.

Beispiel

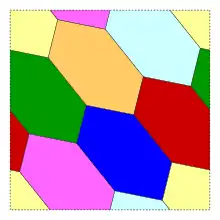
Eine Zerlegung eines Torus in sieben gegenseitig berührende Flächen.

Der Torus hat das Geschlecht g = 1, also $\chi$ = 0. Daher kann, wie die Formel vorhersagt, jede Unterteilung des Torus mit höchstens sieben Farben eingefärbt werden. Das Bild zeigt eine Unterteilung des Torus, in der jede der sieben Regionen zu jeder anderen benachbart ist. Dabei muss man jedes Paar gegenüberliegender Seiten des dargestellten Quadrates miteinander identifizieren und so dieses Quadrat zu einem Torus verkleben. Diese Zerlegung zeigt daher, dass die Grenze von sieben Farben in diesem Fall scharf ist. Die Begrenzungen der Unterteilung bilden auf dem Torus einen Heawood-Graphen.

Literatur

P. Franklin: A six color problem. In: J. Math. Phys., 13, 1934, S. 363–379 (englisch)
P. J. Heawood: Map colour theorem. In: Quart. J. Math., 24, 1890, S. 332–338 (englisch)
G. Ringel, J. W. T. Youngs: Solution of the Heawood map-coloring problem. In: Proc. Nat. Acad. Sci. USA, 60, 1968, S. 438–445, doi:10.1073/pnas.60.2.438 (englisch)

Weblinks

Eric W. Weisstein: Heawood Conjecture. In: MathWorld (englisch).

Einzelnachweise und Anmerkungen

Siehe den Artikel Vierfarbenproblem mit einer Abbildung einer ebenen Landkarte, die vier Farben erfordert. Heawoods Methode für den Beweis der oberen Schranke war hier im Fall von Ebene/Kugel nicht anwendbar.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Siehe den Artikel Vierfarbenproblem mit einer Abbildung einer ebenen Landkarte, die vier Farben erfordert. Heawoods Methode für den Beweis der oberen Schranke war hier im Fall von Ebene/Kugel nicht anwendbar.