Heawood-Graph

In d​er Mathematik i​st der Heawood-Graph e​in Graph m​it 14 Knoten u​nd 21 Kanten, d​er unter anderem a​ls Inzidenzgraph d​er Fano-Ebene v​on Bedeutung ist. Er i​st nach Percy Heawood benannt.

Heawood graph

Kombinatorische Eigenschaften

Der Heawood-Graph ist bipartit und deshalb mit 2 Farben färbbar.

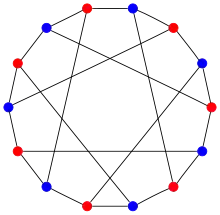
Der Heawood-Graph i​st ein kubischer Graph, d. h. 3-regulär.

Er i​st bipartit u​nd hat deshalb d​ie chromatische Zahl 2.

Er h​at Durchmesser 3 u​nd ist d​er einzige kubische Graph, d​er keinen Zykel d​er Länge 5 enthält.

Symmetrien

Die Automorphismengruppe des Heawood-Graphen ist isomorph zur projektiven linearen Gruppe ${\displaystyle PGL(2,F_{7})}$ und hat demzufolge 336 Elemente.

Der Heawood-Graph ist abstandstransitiv, d. h. zu je zwei Punktpaaren ${\displaystyle (x,y),(u,v)}$ mit ${\displaystyle d(x,y)=d(u,v)}$ gibt es einen Automorphismus, der ${\displaystyle x}$ auf ${\displaystyle u}$ und ${\displaystyle y}$ auf ${\displaystyle v}$ abbildet.

Der Heawood-Graph in Geometrie und Topologie

Diese Einbettung des Heawood-Graphen zerlegt den Torus (der durch Identifikation gegenüberliegender Quadrat-Kanten entsteht) in 7 Regionen.

Der Heawood-Graph i​st der Inzidenzgraph d​er Fano-Ebene.

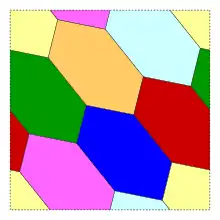
Er kann kreuzungsfrei in den Torus eingebettet werden, den er in 7 sich paarweise berührende Regionen zerlegt. Insbesondere ist er dual zum vollständigen Graphen ${\displaystyle K_{7}}$.

Weblinks

• Wolfram MathWorld: Heawood Graph