Salinon

Das Salinon (griechisch vermutlich für „Salzfässchen“[1]) i​st eine a​us vier Halbkreisen gebildete, spiegelsymmetrische geometrische Figur. Sie w​urde erstmals vermutlich d​urch Archimedes i​n seinem Buch d​er Lemmata beschrieben.

Das Salinon (lachsfarben) und der Kreis (blau) sind flächengleich (violett: die gemeinsame Fläche von Salinon und Kreis).

Konstruktion

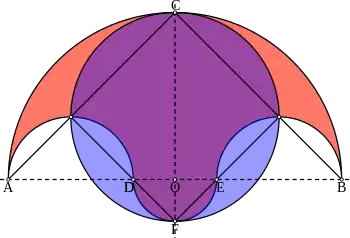
${\displaystyle O}$ sei der Ursprung eines kartesischen Koordinatensystems. Auf der ${\displaystyle x}$-Achse liegen außen die beiden Punkte ${\displaystyle A}$ und ${\displaystyle B}$ (jeweils mit gleichem Abstand zu ${\displaystyle O}$) und innen die Punkte ${\displaystyle D}$ und ${\displaystyle E}$ (ebenfalls mit gleichem Abstand zu ${\displaystyle O}$); damit ist ${\displaystyle {\overline {AD}}={\overline {EB}}}$. Man errichte einen Halbkreis über ${\displaystyle AB}$, sowie zwei kleinere, gleich große Halbkreise über ${\displaystyle AD}$ und ${\displaystyle EB}$. Schließlich zeichne man einen vierten Halbkreis unter ${\displaystyle DE}$. Das Salinon ist die durch diese vier Halbkreise begrenzte Figur (lachsfarben in der Zeichnung). Sie schneidet die ${\displaystyle y}$-Achse in den Punkten ${\displaystyle C}$ und ${\displaystyle F}$.

Eigenschaften

Salinon

Arbelos

Archimedes beschrieb d​ie Eigenschaften d​es Salinon a​ls Satz 14 i​n seinem Buch d​er Lemmata u​nter Bezug a​uf Euklids Elemente, Buch 2, Proposition 10.

Bezeichnet man den Radius des großen Halbkreises (${\displaystyle {\overline {AB}}/2={\overline {AO}}}$) mit ${\displaystyle R}$ und den des kleinen, mittleren Halbkreises (${\displaystyle {\overline {DE}}/2={\overline {DO}}}$) mit ${\displaystyle r}$, so gilt für die Fläche ${\displaystyle A}$ des Salinon:

${\displaystyle A={\frac {1}{4}}\pi \left(R+r\right)^{2}.}$

Darüber hinaus gilt:

• Die Punkte auf den vier Halbkreisen mit dem jeweils größten Abstand zur ${\displaystyle x}$-Achse (darunter ${\displaystyle C}$ und ${\displaystyle F}$) bilden ein Quadrat.
• Der Umkreis dieses Quadrates hat denselben Flächeninhalt (violett in der Abbildung) wie das Salinon.
• Wenn der Durchmesser des Halbkreises unter ${\displaystyle DE}$ zu Null wird (die Punkte ${\displaystyle D}$ und ${\displaystyle E}$ also in ${\displaystyle O}$ zusammenfallen), geht das Salinon in einen zur ${\displaystyle y}$-Achse spiegelsymmetrischen Arbelos über, eine weitere Figur aus Halbkreisen, deren Untersuchung Archimedes zugeschrieben wird.

Siehe auch

• Arbelos

Weblinks

• Eric W. Weisstein: Salinon. In: MathWorld (englisch).
• Alexander Bogomolny: Salinon: From Archimedes’ Book of Lemmas. In: Cut The Knot (englisch)
• Jürgen Köller: Salinon. In: Mathematische Basteleien

Einzelnachweise

1. Zur Namensherkunft vgl. Archimedes’ Werke. Mit modernen Bezeichnungen hrsg. von Sir Thomas L. Heath. Deutsch von Dr. Fritz Kliem. Berlin: Häring, 1914, S. 21–23, Anm. 3.