SKO (Bionik)

Das SKO-Verfahren (Soft Kill Option)[1] basiert, wie das CAO-Verfahren (CAO: Computer Aided Optimization), auf der Simulation der Wachstumsregel von biologischen Kraftträgern und ist demnach eine Methode aus dem Bereich der Bionik. Das biologische Vorbild ist das Knochenwachstum.

Im Gegensatz zum CAO-Verfahren wird jedoch die Wachstumsregel nicht nur auf die Oberfläche eines Bauteils angewendet, sondern auch auf den inneren Bereich. Das bedeutet, dass Löcher innerhalb des Bauteils entstehen können. Da sich durch das Einbringen von Löchern mathematisch gesehen die Topologie des Bauteils ändert, spricht man bei dieser Art der Optimierung von Topologieoptimierung. Dabei ist es ein besonderes Merkmal der Topologieoptimierung, dass die Löcher nicht über die Form des Netzes des Finite-Elemente-Modells (FEM) abgebildet, sondern innerhalb des Netzes über eine Materialeigenschaft der einzelnen Elemente, den E-Modul simuliert werden. Der E-Modul ist ein Maß für die Steifigkeit und kann in jedem Element des FEM-Netzes individuell variiert werden. Ist der E-Modul sehr klein, ist das Element sehr weich und verhält sich dadurch physikalisch wie ein Loch. Hat es dagegen den Wert des verwendeten Materials, ist es massiv und zeigt das gewünschte Materialverhalten. Die Wachstumsregel bestimmt dabei, welchen Wert die einzelnen Elemente erhalten oder, in anderen Worten, wo Löcher entstehen sollen und wo nicht. Das Maß ist dabei – wie beim CAO-Verfahren – die Differenz zwischen der Spannung des einzelnen Elements $\sigma$ und der Referenzspannung $\sigma _{\text{ref}}$ . Sie dient als Maß dafür, wie stark und in welcher Richtung der E-Modul in einem Wachstumszyklus modifiziert werden muss.

E^{\text{neu}}\sim =E^{\text{alt}}+s(\sigma -\sigma _{\text{ref}})

[2]

Der Skalierungsfaktor ${s}$ beeinflusst die Konvergenzgeschwindigkeit. Am Anfang einer Optimierung wird der Wert über den Quotient aus maximalen E-Modul und Referenzspannung ( $E^{\text{max}}$ / $\sigma _{\text{ref}}$ ) bestimmt.[3] Das Verfahren wird abgebrochen, wenn sich eine stabile Struktur herausgebildet hat. Da bei SKO die biologische Wachstumsregel simuliert wird, liefert dieses Verfahren eine Struktur mit homogener Oberflächenspannung. Es ist demnach, wie CAO, für Festigkeitsprobleme geeignet.

Auf Grund der Tatsache, dass die Form bei der Topologieoptimierung allein über die Verteilung einer Materialeigenschaft beschrieben wird, ist diese Art von Optimierung sehr flexibel. Da jedoch das Material nur elementweise hinzugefügt oder entfernt werden kann, erhält man im Gegensatz zum CAO-Verfahren kein detailliertes Design, sondern einen Designvorschlag, der sehr grob sein kann. Weiterhin kommt erschwerend hinzu, dass das ermittelte Design nicht nur Elemente mit maximalem und minimalem E-Modul aufweist, sondern auch solche mit Zwischenwerten. Um den massiven Bereich graphisch darstellen zu können, muss der Anwender deswegen festlegen, ab welcher Grenze ein Element als massiv anzusehen ist.

Anwendungen

Man kann drei Anwendungsbereiche der Topologieoptimierung unterscheiden. Die einfachste Anwendung ist die Bestimmung der Lage und Form von Löchern in Bauteilen um deren Gewicht zu reduzieren. Der zweite Einsatzbereich ist das Auffinden der bestmöglichen Anordnung von Sicken in Blechen. Der dritte Anwendungsbereich ist die Bestimmung der optimalen Merkmale von Bauteilen oder Bauteilgruppen. Damit kann man in der Konzeptphase ermitteln, in welchen Bereichen Material benötigt wird oder wo Strukturen aufgebaut werden müssen. Weiterhin kann man jedoch auch sehr detailliert den optimalen Querschnitt und die optimale Anzahl und Anordnung von Rippen bei Gussteilen bestimmen.

Das SKO-Verfahren hat sich vor allem bei der Optimierung von Gussteilen bewährt. Die Erfahrung zeigt, dass bei Gussteilen die Ermittelung von optimalen Merkmalen von höchster Wichtigkeit ist. Sind diese bei einem Bauteil nicht optimal, kann eine Formoptimierung das Bauteil meistens nur unwesentlich verbessern. Die optimalen Merkmale sind somit die Basis für ein optimales Bauteil und legen das Optimierungspotential erst fest.

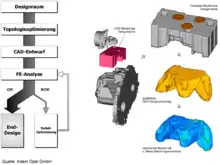
Designprozess, in dem am Anfang die Topologieoptimierung steht und erst danach unter Verwendung des Designvorschlags eine Konstruktion des Bauteils erfolgt

Der Ablauf einer solchen Gussteiloptimierung ist in der Abbildung dargestellt. Statt eines detaillierten Bauteils generiert der Konstrukteur im ersten Schritt nur ein CAD-Modell des zur Verfügung stehenden Bauraums, auch Designraum genannt. Basierend auf dem Designraum wird eine Topologieoptimierung durchgeführt, um die wichtigsten Merkmale des Bauteils festzulegen, wie beispielsweise Querschnitt und Rippenanordnung. Erst dann wird ein detailliertes CAD-Modell des Bauteils erstellt, das zur Kontrolle noch berechnet und gegebenenfalls feinoptimiert wird.

Die Umsetzung des Designvorschlags ist immer der schwierigste Schritt und die besondere Herausforderung bei einer Topologieoptimierung, weil man aus dem Designvorschlag ein Bauteil herleiten muss, dass auf der einen Seite gießbar ist, auf der anderen Seite jedoch möglichst nahe an den Designvorschlag herankommen soll. Da ein Knochen kein Problem mit Fertigungsrestriktionen hat, sondern einfach in die optimale Form hineinwächst, liefert die Wachstumsregel in der Regel Designvorschläge, die sich fertigungstechnisch nie direkt umsetzen lassen. Um diese Situation zu verbessern, wurde TopShape entwickelt, bei dem neben der biologischen Wachstumsregel zusätzlich die einfachsten Fertigungsrestriktionen für Gussteile mit berücksichtigt werden.[4]

Literatur

C. Mattheck: Design in der Natur. Rombach GmbH + Co Verlagshaus KG, Freiburg i. B., 1997, ISBN 3793091503
Baumgartner, L. Harzheim, C. Mattheck: SKO (Soft Kill Option): The Biological Way to Find an Optimum Structure Topology. Int J Fatigue 14 No 6, 1992, 387–393
L. Harzheim, G. Graf: A Review of Optimization of Cast Parts Using Topology Optimization: I - Topology Optimization without Manufacturing Constraints. Struct Multdisc Optim 30, 2005, 491–497
L. Harzheim: Strukturoptimierung, Grundlagen und Anwendungen. Wissenschaftlicher Verlag Harri Deutsch GmbH, Frankfurt am Main, 2007, ISBN 978-3-8171-1809-0
A. Sauer: Bionik in der Strukturoptimierung - Praxishandbuch für ressourceneffizienten Leichtbau. Vogel-Fachbuch Verlag, Würzburg, 2018, ISBN 978-3-8343-3381-0

Einzelnachweise

C. Mattheck: Design in der Natur. Rombach GmbH + Co Verlagshaus KG, Freiburg i. B., 1997, ISBN 3793091503
A. Sauer: Bionik in der Strukturoptimierung - Praxishandbuch für ressourceneffizienten Leichtbau. Vogel-Fachbuch Verlag, Würzburg, 2018, ISBN 978-3-8343-3381-0
Baumgartner, L. Harzheim, C. Mattheck: SKO (Soft Kill Option): The Biological Way to Find an Optimum Structure Topology. Int J Fatigue 14 No 6, 1992, 387–393
L. Harzheim: Strukturoptimierung, Grundlagen und Anwendungen. Wissenschaftlicher Verlag Harri Deutsch GmbH, Frankfurt am Main, 2007, ISBN 978-3-8171-1809-0

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] C. Mattheck: Design in der Natur. Rombach GmbH + Co Verlagshaus KG, Freiburg i. B., 1997, ISBN 3793091503

[2] A. Sauer: Bionik in der Strukturoptimierung - Praxishandbuch für ressourceneffizienten Leichtbau. Vogel-Fachbuch Verlag, Würzburg, 2018, ISBN 978-3-8343-3381-0

[3] Baumgartner, L. Harzheim, C. Mattheck: SKO (Soft Kill Option): The Biological Way to Find an Optimum Structure Topology. Int J Fatigue 14 No 6, 1992, 387–393

[4] L. Harzheim: Strukturoptimierung, Grundlagen und Anwendungen. Wissenschaftlicher Verlag Harri Deutsch GmbH, Frankfurt am Main, 2007, ISBN 978-3-8171-1809-0