Topologieoptimierung
Die Topologieoptimierung ist ein computerbasiertes Verfahren, durch welches eine günstige Grundgestalt (Topologie) für Bauteile unter mechanischer Belastung berechnet werden kann. Sie wird im Bauingenieurwesen, der Luft- und Raumfahrttechnik, im Automobil- und Fahrzeugbau und in anderen Sparten des Maschinenbaus eingesetzt. Auf Grund des Top-Down-Ansatzes zur Reduktion nicht benötigten Materials, ist die Topologieoptimierung verwandt mit der Bionik, die sich mit der Nachahmung der Natur beschäftigt.
Ausgangspunkt des Verfahrens ist ein geometrischer Körper, welcher den Raum darstellt, der für das zu entwickelnde Bauteil maximal zur Verfügung gestellt werden soll. Dieser Körper wird als „Bauraum“ bezeichnet. Die Berechnung zeigt auf, welche Partien des Bauraums mit Werkstoff belegt werden sollen.[1]
Für den Berechnungsablauf muss wiederholt die Beanspruchungsverteilung im Bauraum bestimmt werden. Dazu setzen Programme zur Topologieoptimierung heute üblicherweise die Finite-Elemente-Methode (FEM) ein. Während einige Implementierungen eigene Module für die FEM-Berechnung enthalten, ist für andere die Einbindung eines externen FEM-Programms erforderlich.
Kontinuierliche und diskrete Topologieoptimierung
Man kann kontinuierliche und diskrete Topologieoptimierung unterscheiden. Bei der kontinuierlichen Topologieoptimierung wird die Materialverteilung im Bauraum gesucht. Bei der diskreten Topologieoptimierung werden diskrete Elemente als Überdeckung des Bauraums gesucht. Beispielsweise kann ein optimales Fachwerk gesucht werden, welches letztlich eine Topologie des Gesamtobjekts darstellt.
Kontinuierliche Topologieoptimierung
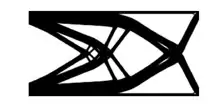
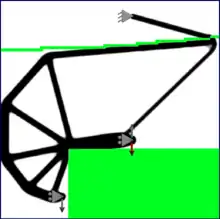
In der Konstruktion wird die Topologieoptimierung eingesetzt, um Vorschläge für Erstentwürfe von Bauteilen zu erhalten. Dabei muss der Konstrukteur zuerst den maximal zur Verfügung stehenden Bauraum und die Randbedingungen (Lasten und Einspannungen) festlegen. Diese Daten werden in ein FE-Modell (FE = Finite Elemente) umgesetzt.
Grundsätzlich wird nach materieller und geometrischer Topologieoptimierung unterschieden. In der geometrischen Topologieoptimierung wird die Geometrie des Bauteils durch die Form der Außenberandung (äußerster Rand), also der Kanten und Oberflächen beschrieben. Dabei werden auch Aussparungen innerhalb der Bauteilberandung vorgenommen und in ihrer Form variiert. In der materiellen Topologieoptimierung wird die Geometrie eines Bauteils im Entwurfsraum beschrieben. Hierbei wird jedem finiten Element im Entwurfsraum eine Dichte zugewiesen. Bei einfachen Optimierungsalgorithmen wie den Optimalitätskriterien (z. B. Fully Stressed Design) wird die Dichte wie ein einfacher Ein-/Ausschalter entweder auf 0 oder auf 100 Prozent gesetzt. Bei Fully Stressed Design bleiben die Elemente erhalten, die nahe der maximal zulässigen Spannung beansprucht werden, so dass am Ende der Optimierung nahezu jedes Element des FE-Netzes hinsichtlich der Festigkeit vollständig ausgenutzt wird. Bei der mathematischen Programmierung handelt es sich um einen Optimierungsalgorithmus, der durch die partiellen Ableitungen der Zielfunktion die Änderung der einzelnen Parameter für die nächste Iteration bestimmt. Demnach muss hierbei eine stetige Dichteverteilung für eine Differenzierbarkeit vorliegen. Dabei wird in der so genannten Homogenisierungsmethode die Änderung der Dichte durch einen mikroskopischen Hohlkörper in jedem der Finiten Elemente beschrieben und anschließend über ein nichtlineares makroskopisches Materialgesetz in eine Änderung des E-Moduls überführt. Dadurch lassen sich die Spannungen und Verformungen des Bauteils berechnen. Als Ergebnis einer solchen Topologieoptimierung erhält man ein zerklüftetes, poröses Entwurfsmodell, das aufgrund der knochenartigen Struktur und der Vernachlässigung von Fertigungsrestriktionen nur eine Hilfe zur Gestaltfindung bietet. Eine Möglichkeit zur Verbesserung des Ergebnisses ist die Rückführung des FE-Modells in ein geglättetes CAD-Flächenmodell. Hierbei lassen sich ggf. auch Fertigungsrestriktionen berücksichtigen.
Diskrete Topologieoptimierung
Eine der ersten Topologieoptimierungen wurde von Anthony George Maldon Michell durchgeführt.[2] Aber auch heute noch werden Topologieoptimerungen durch Stabwerke durchgeführt.[3] Der Grund hierfür liegt in der geringen Rechenzeit; wenngleich das Ergebnis deutlich weniger realistisch ist als bei der kontinuierlichen Topologieoptimierung.
Siehe auch
Weblinks
- Beispiele zur kontinuierlichen Topologieoptimierung (englisch)
- Beispiele zur diskreten Topologieoptimierung mittels Stabwerk (englisch)
- Beispiele und Animationen (englisch)
Einzelnachweise
- Bendsøe M.P., Sigmund, O.: Topology Optimization - Theory, Methods and Applications. ISBN 978-3-540-42992-0.
- Michell A. G. M. (1904) The limits of economy of material in frame structures. Philosophical Magazine 8(47):589–597 doi:10.1080/14786440409463229.
- Bendsøe M. P., Ben-Tal A., Zowe J. (1994): Optimization methods for truss geometry and topology design. Structural and Multidisciplinary Optimization 7:141–159, doi:10.1007/BF01742459.