Computer Aided Optimization

Das CAO-Verfahren (Computer Aided Optimization) ist ein Verfahren zur Formoptimierung aus dem Bereich der Bionik, bei dem das Wachstumsverhalten von biologischen Kraftträgern (wie z. B. Bäume, Knochen) nachgebildet wird. Die Idee ist dabei, dass man die Oberfläche des zu optimierenden Bauteils gemäß der biologischen Wachstumsregel virtuell wachsen lässt, wie es beispielsweise ein Knochen tun würde, wenn er die Funktion des Bauteils übernehmen müsste. Da die Wachstumsregel zu einer Form mit homogener Oberflächenspannung führt, kann das Verfahren zum Abbau von Spannungsspitzen und damit zur Erhöhung der Festigkeit eingesetzt werden. In der Regel wird jedoch nicht die gesamte Oberfläche eines Bauteils dem Optimierungsprozess unterworfen, sondern nur die kritischen Bereiche, die vom Anwender zuvor identifiziert worden sind. Die Basis für die Simulation der biologischen Wachstumsregel sind die Spannungen in dem zu optimierenden Bauteil, die mit Hilfe eines Finite-Elemente-Modells (FEM) berechnet werden. Dabei wird die Geometrie des zu optimierenden Bauteils allein über das FEM-Netz, oder – besser gesagt – durch die Lage der Knoten auf der Oberfläche beschrieben.

Der prinzipielle Ablauf des CAO-Verfahrens ist in Abb. 1 dargestellt. Zu Beginn steht eine FEM-Analyse, in der die Spannungen im Bauteil berechnet werden. Basierend auf den Spannungswerten wird die biologische Wachstumsregel simuliert und eine daraus resultierende Wachstumsverschiebung bestimmt. Die neue Kontur erhält man, indem man die Wachstumsverschiebungen zu den entsprechenden aktuellen Koordinaten hinzuaddiert. Im nächsten Schritt wird eine Netzkorrektur durchgeführt, um das Netz an die neue Kontur anzupassen und um Netzverzerrungen so gering wie möglich zu halten. Danach ist ein Wachstumszyklus abgeschlossen und die nächste Iteration kann mit der Spannungsanalyse für die modifizierte Struktur begonnen werden. Das Verfahren wird abgebrochen, wenn die erwünschte homogene Oberflächenspannung erreicht ist oder geometrische Restriktionen weiteres Wachstum verbieten.

Es gibt zwei Versionen für die Simulation der biologischen Wachstumsregel. Bei der ursprünglichen Version des CAO-Verfahrens, die am Forschungszentrum Karlsruhe entwickelt wurde, wird die Wachstumsregel mit Hilfe einer Wachstumsschicht (auch Schwellschicht genannt) simuliert. Diese wird in dem zu optimierenden Bereich unterhalb der Außenkontur aufgebracht und sollte eine möglichst konstante Dicke aufweisen. Die Wachstumsverschiebungen werden in einer zusätzlichen FEM-Analyse berechnet, in der die Wachstumsschicht, die einen wesentlich geringeren E-Modul als die darunterliegende Struktur zugewiesen bekommt, einem volumetrischen Schwellgesetz unterworfen wird. Dabei wird in der Wachstumsschicht eine Temperaturverteilung der Art aufgebracht, dass sie in den unterbelasteten Bereichen zu einem Zusammenziehen und damit zu einem Abbau von Material führt, während sich die Schicht in den hochbelasteten Bereichen ausdehnt und damit Material angelagert wird. Bei der Verwendung der Wachstumsschicht tritt das Problem auf, dass bei komplexen CAD-Modellen die Modellierung der Wachstumsschicht mit erheblichem Aufwand verbunden ist.

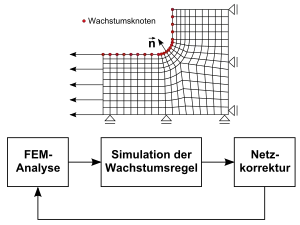
Abb. 1: Das CAO-Verfahren (direkte Methode)

Bei der direkten Methode besteht das Modellierungsproblem nicht mehr, weil auf eine Wachstumsschicht verzichtet wird und die Wachstumsverschiebungen direkt berechnet und auf die Knoten aufgebracht werden. Man kann damit ein bestehendes FEM-Netz ohne Modifikationen verwenden. Weiterhin wird die FEM-Analyse für die Simulation des Schwellgesetzes eingespart. Zu Beginn der Optimierung definiert der Anwender die Oberflächenknoten in den Bereichen, die in der Form variiert werden sollen, als 'Wachstumsknoten'. Für jeden dieser Wachstumsknoten wird mit Hilfe der Knotenpunktsspannung $\sigma _{k}^{(i)}$ eine Wachstumsverschiebung ${\vec {d}}_{k}^{(i)}$ berechnet:

${\vec {d}}_{k}^{(i)}=s(1+\alpha )(\sigma _{k}^{(i)}-\sigma _{\text{ref}}){\vec {n}}_{k}^{(i)}$ . (1)

Dabei ist $s$ ein Skalierungsfaktor, der so gewählt werden sollte, dass sich im ersten Schritt die maximale Spannung im Variationsbereich um ungefähr die Hälfte reduziert. Der Richtungsvektor ${\vec {n}}_{k}^{(i)}$ ist nach außen orientiert und in der Regel in Richtung der Flächennormalen ausgerichtet. Er gibt die Richtung der Wachstumsverschiebung vor. Die Referenzspannung $\sigma _{\text{ref}}$ legt fest, welcher Knoten als hoch belastet ( $\sigma _{k}^{(i)}>\sigma _{\text{ref}}$ ) und welcher als niedrig belastet ( $\sigma _{k}^{(i)}<\sigma _{\text{ref}}$ ) gilt. Sie ist auch die Spannung, die sich am Ende der Optimierung als homogene Oberflächenspannung einstellt. In der Regel müssen bei der Optimierung mehrere Lastfälle berücksichtigt werden. In diesem Fall wird für jeden Wachstumsknoten die maximale Spannung aus allen Lastfällen verwendet. Man sieht leicht, dass Gleichung (1) gerade das erwünschte Wachstumsverhalten beschreibt, da im Falle der hohen Belastung die Wachstumsverschiebung nach außen gerichtet ist und damit Material angelagert wird, während sie bei niedriger Belastung nach innen zeigt und somit Material entfernt wird. Der Korrekturfaktor $\alpha$ bewirkt an starken Ecken eine Glättung der neuen Kontur und verhindert die Bildung von Knicken.

An zahlreichen Beispielen aus der Natur konnte überprüft und nachgewiesen werden, dass das CAO-Verfahren zu den beobachteten Strukturen der biologischen Kraftträger führt und zudem auch Wachstumsverhalten wie beispielsweise das Wandern und Drehen von Knochentrabekeln simulieren kann.

Anwendungen

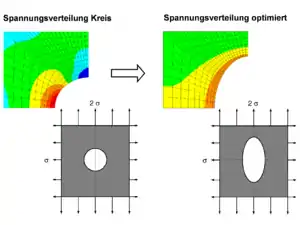
Abb. 2: Formoptimierung einer bi-axial belasteten Lochplatte. Bei der Berechnung der Spannungen wurde die Symmetrieeigenschaft ausgenutzt und nur ein Viertel der Platte modelliert. Durch Spiegelung dieses Viertels an den beiden Spiegelebenen (gestrichelte Linien) erhält man die gesamte Spannungsverteilung

In Abb. 2 ist als einfaches Anwendungsbeispiel die Optimierung der Lochform einer bi-axial belasteten Lochplatte dargestellt. Ziel war es eine Form mit homogener Spannung entlang des Lochrandes zu finden. Diese wurde nach 10 Wachstumszyklen erreicht. Die gezeigte Lochplatte entspricht mechanisch gesehen ungefähr einem Astloch in einem Baum, das auch länglich und nicht kreisförmig zusammenwächst.

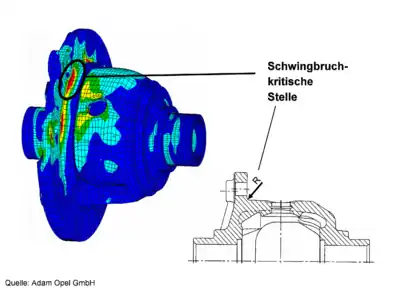
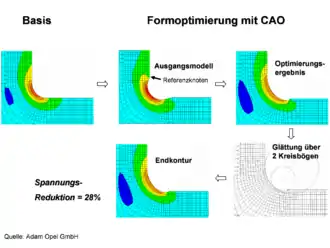
Als weiteres Anwendungsbeispiel ist in Abb. 3 und 4 die Optimierung eines Hinterachsdiffentials gezeigt. Dort lag am Flansch zur Befestigung des großen Kegelrads eine schwingbruchkritische Stelle vor. Der Radius bei der dort verwendeten Verrundung von R=2 mm konnte nicht weiter vergrößert werden, um die Spannung abzusenken. Beginnend mit einem Hinterschnitt mit R=3 mm wurde deshalb eine Optimierung mit dem CAO-Verfahren durchgeführt. Die optimierte Kontur wurde dann durch zwei Kreissegmente mit den Radien von R=2,5 mm und R=5,5 mm angenähert. Diese kann sowohl mittels Drehen als auch mittels Schleifen gefertigt werden. Es ergab sich eine Spannungsreduktion von 28 %.

Abb. 3: Querschnitt und Spannungsverteilung eines Differentialkäfigs vor der Optimierung

Abb. 4: Zwischenschritte der Formoptimierung ausgehend vom Hinterschnitt (Ausgangsmodell) bis zur optimierten Kontur und über die Glättung bis zur optimierten Endkontur im schwingbruchkritischen Bereich. Zum Vergleich ist links die Form- und Spannungsverteilung der Basiskontur aus Abb. 3 gezeigt

Literatur

C. Mattheck: Design and Growth Rule for Biological Structures and their Application in Engineering. Fatigue Fract Eng Mater Struct 13, 5, 1990, 535–550.
C. Mattheck: Design in der Natur. Rombach GmbH + Co Verlagshaus KG, Freiburg i. B., 1997, ISBN 3793091503
C. Mattheck: Engineering Components Grow Like Trees. Mat.-wiss. U. Werkstofftech. 21, 1990, 143–168
L. Harzheim: Optimierung von Bauteilen mit der Wachstumsregel von Bäumen und Knochen. BIONA Report 16, Akad. Wiss. Lit., Mainz, 2003, 83–94
H. Bubenhagen, L. Harzheim: Einsatz der Formoptimierung zur Lebensdauerverbesserung von Bauteilen. Konstruktion 50 1998 H. 11/12, 1998, 40–44
L. Harzheim: Strukturoptimierung, Grundlagen und Anwendungen. Wissenschaftlicher Verlag Harri Deutsch GmbH, Frankfurt am Main, 2007, ISBN 978-3-8171-1809-0

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.