Robinson-Crusoe-Wirtschaft

Die Robinson-Crusoe-Wirtschaft, aufbauend auf dem Roman „Robinson Crusoe“ von Daniel Defoe aus dem Jahr 1719, beschreibt eine Ein-Personen-Wirtschaft mit einem Konsumenten, einem Produzenten und zwei Gütern die zur Verfügung stehen.

Der Roman handelt von einem schiffbrüchigen, schottischen Seemann, der auf einer einsamen Insel für mehrere Jahre strandet.

Diese Geschichte wird oft als internationales Wirtschaftsmodell verwendet, da es die ökonomischen Zusammenhänge der Realität vereinfacht darstellt und man von diesem Modell auf komplexere Modelle schließen kann. Zum Beispiel um von einer Ein-Personen-Wirtschaft mit nur einem Agierenden auf mehrere Agierende zu schließen.[1] Das Modell wird auch in der Finanzwissenschaft, in der Wachstumstheorie und in der Mikroökonomik, auf welcher dieser Artikel aufbaut, verwendet.

In der Robinson-Crusoe-Wirtschaft nimmt man an, dass Robinson der einzige wirtschaftlich Handelnde ist. Dies bedeutet, dass er als Produzent seinen Profit maximiert und auch als Konsument seinen Nutzen maximiert. Des Weiteren wird angenommen, dass alle Güter aus bestehenden Vorräten auf der Insel produziert oder gefunden werden müssen und dass die Insel von der restlichen Welt abgegrenzt ist und somit kein Handel besteht. Die herrschenden Zustände ändern sich jedoch bei Einführen einer weiteren Person -Freitag- wie es auch Grundlage des Romans ist.

Robinson als Einsiedler

Transformationskurve von Robinson nach Gütern Kokosnuss und Fisch

Robinson als Einsiedler bedeutet, dass er alleine auf einer Insel gestrandet ist und zum Überleben arbeiten muss. Hier wird beispielhaft angenommen, dass es nur Kokosnusspalmen gibt und im Meer Fische leben. Des Weiteren kann Robinson eine bestimmte Anzahl an Stunden am Tag arbeiten, um Fische zu fangen und Kokosnüsse zu sammeln.

Robinson kann beispielsweise 8 Stunden am Tag arbeiten. Somit weiß er, dass er 20 Fische pro Woche fangen kann, wenn er keine Kokosnüsse sammelt. Umgekehrt kann er 40 Kokosnüsse sammeln, wenn er auf das Fischen verzichtet. Selbstverständlich kann Robinson auch zwischen den beiden Gütern variieren. Er kann beispielsweise 10 Fische fangen und 20 Nüsse sammeln. Diese Güterkombinationen lassen sich grafisch in einem Koordinatensystem abtragen. Dabei beschränkt sich die Y-Achse auf die Menge der Nüsse und die Menge der Fische auf die X-Achse.

In Punkt A fängt Robinson sieben Tage lang nur Fische und erhält somit 20 Fische und null Kokosnüsse.

In Punkt B sammelt Robinson eine Woche lang nur Kokosnüsse und erhält 40 Nüsse und null Fische. Durch die Verbindung dieser beiden Punkte entsteht die Produktionsmöglichkeitenkurve, die auch Transformationskurve genannt wird. Alle Punkte, die auf dieser Geraden liegen, sind realisierbar und effizient. Alle Punkte, die unterhalb dieser Geraden liegen, sind realisierbar, aber ineffizient. Alle Punkte oberhalb dieser Geraden sind nicht realisierbar.

Für welche Kombination sich Robinson entscheidet, hängt von seinen Präferenzen ab, das heißt ob er lieber mehr Kokosnüsse oder mehr Fische essen möchte.

Die Steigung der Kurve gibt die Grenzrate der Transformationskurve wieder, das heißt wie viel Robinson von einem Gut erhält, wenn er auf das andere Gut verzichtet, auch bekannt als Opportunitätskosten.

Die Form dieser Kurve ist abhängig von der verwendeten Technologie und der Anzahl der Ressourcen.
Vor allem aber kommt es auf die Art der Skalenerträge in der Technologie an. Liegen abnehmende Skalenerträge vor, ist die Transformationskurve konkav, liegen aber zunehmende Skalenerträge vor, verläuft die Kurve konvex, jeweils zum Ursprung. Herrschen jedoch konstante Skalenerträge und zusätzlich wird nur ein Input in der Produktion verwendet, so ist die Transformationskurve linear.[2]

Herleitung der linearen Transformationskurve:
Verhältnis zwischen Produkt (z. B. Gut Fisch= $x_{1}$ ) und dem, dazu benötigen Arbeitseinsatz $A_{1}$ wird durch eine Produktionsfunktion abgebildet

(1).

{x_{1}}={\frac {A_{1}}{a_{1}}}

$a_{1}$ = Verbrauchskoeffizient, der angibt, wie viel Arbeitszeit Robinson benötigt, um eine Einheit der Gesamtproduktion zu erstellen.

Beispiel: 1 Fisch = (1/20) Woche

Die bei einer gegebenen Gesamtproduktion $x_{1}$ maximal mögliche Gesamtproduktion an Nüssen (Gut $x_{2}$ ) lässt sich dann als Quotient aus dem noch vorhandenen Arbeitszeitinput ([B] – A₁) durch den Verbrauchskoeffizienten von $a_{2}$ berechnen:

(2).

{x_{2}}={\frac {[B]-A_{1}}{a_{2}}}

Durch die Umformung der Gleichung (1.) erhält man für $A_{1}$ :

(3).

{A_{1}}=x_{1}a1\,

Durch Einsetzen von (3.) und (2.) erhält man:

(4.)

{x_{2}}={\frac {[B]-x_{1}a_{1}}{a_{2}}}\,

Durch Umformung erhält man die letzte Gleichung:

(5.)

{x_{2}}={\frac {[B]}{a_{2}}}-{\frac {a_{1}}{a_{2}}}\ x_{1}

[3]

Optimaler Arbeitseinsatz von Robinson

Der optimale Arbeitseinsatz von Robinson

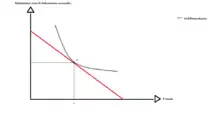
Je mehr Robinson arbeitet, desto weniger Freizeit steht Robinson zur Verfügung. Somit wählt Robinson zwischen Arbeit und Freizeit.
Robinson hat zwei Möglichkeiten: Einkünfte erwirtschaften, durch das Sammeln von Kokosnüssen (abgetragen auf der Y-Achse) oder durch das konsumieren von Freizeit (abgetragen auf der X-Achse). Wie bei der Wahl zwischen zwei Gütern, muss Robinson auch hier entscheiden zwischen:

Mehr zu arbeiten und dadurch mehr Kokosnüsse zu sammeln und somit auf mehr Freizeit zu verzichten oder
vice versa mehr Freizeit zu konsumieren und dabei auf Kokosnüsse zu verzichten.

Punkt A gibt den optimalen Trade-off zwischen Nachfrage nach Freizeit und Angebot nach Arbeit wieder, welches der Tangentialpunkt der Indifferenzkurve und der Geraden ist.[4][5] Die Indifferenzkurve gibt die Kombination an Gütern wieder, welche den gleichen Nutzen aufweisen und somit den Konsumenten indifferent zwischen der Wahl dieser Kombinationen macht. Sie hat dieselbe Steigung wie die Grenzrate der Substitution, welche das Austauschverhältnis der Güter misst. Das Austauschverhältnis widerspiegelt, auf wie viele beispielsweise Fische Robinson verzichten muss um eine Einheit mehr Kokosnüsse zu erhalten.

Herleitung der Indifferenzkurve:
In allgemeiner Form lautet die Nutzenfunktion $U=U(x_{1},x_{2})$ .
Das daraus gebildete vollständige Differential wird null gesetzt:

(1).

\mathrm {d} U={\frac {\partial \;U(x_{1},x_{2})}{\partial x_{1}}}\mathrm {d} x_{1}+{\frac {\partial \;U(x_{1},x_{2})}{\partial x_{2}}}\mathrm {d} x_{2}=0

Umgestellt ergibt dies die Steigung der Indifferenzkurve:

(2).

{\frac {\mathrm {d} x_{2}}{\mathrm {d} x_{1}}}=-{\frac {\frac {\partial U(x_{1},x_{2})}{\partial x_{1}}}{\frac {\partial U(x_{1},x_{2})}{\partial x_{1}}}}

Daraus wird deutlich, dass die Steigung der Indifferenzkurve aus dem Verhältnis des Grenznutzen bestimmt wird.[6]

Produktionsfunktion und Indifferenzkurve

Der Tangentialpunkt von Robinsons Produktionsfunktion und Indifferenzkurve bei abnehmenden Skalenerträgen

Die Produktionsfunktion gibt die Beziehung zwischen Robinsons Arbeitseinsatz und der Anzahl, der dafür erhaltenen Kokosnüsse wider.[7] Hierbei handelt es sich um eine konkave Funktion, da der zusätzliche Gewinn an Kokosnüssen mit steigenden Arbeitsstunden abnimmt. Dies ist zurückzuführen auf das Grenzprodukt der Arbeit.[8]

Im Punkt (A) tangiert die Indifferenzkurve die Produktionskurve. Hier befindet sich das optimale Gleichgewicht zwischen Arbeit und Freizeit, bei gegebener Technologie, für das Sammeln von Kokosnüssen.

In diesem Gleichgewichtspunkt muss die Grenzrate der Substitution zwischen Freizeit und Kokosnüssen gleich dem Grenzprodukt der Arbeit sein:

GRS=GPA

[7]

Die Doppelrolle von Robinson Crusoe

Die Doppelrolle ist anhand der Annahme, dass Robinson Crusoe simultan nicht mehr Produzent und Konsument ist, zu erklären. Er möchte an einem Tag produzieren und erst am nächsten Tag konsumieren. Um dies optimal koordinieren zu können, gründet er einen Arbeitsmarkt und einen Kokosnussmarkt.
Des Weiteren ist Robinson der einzige Aktieninhaber seiner gegründeten Unternehmung, welche die Gewinnmaximierung anwendet. Dies bedeutet er betrachtet die Nachfrage nach Arbeit und vergleicht sie mit der Menge die produziert werden soll.
Als Aktieninhaber erzielt er Gewinne, welche er als Konsument nutzt, um Produkte der Unternehmung zu kaufen.[7]

Produzent

Produktionsfunktion und Isogewinnlinie von Robinson nach Kokosnüssen und Arbeit

Robinson Crusoe entscheidet am Vortag wie viel Arbeit er am nächsten Tag nachfrägt und wie viele Kokosnüsse er erzeugen möchte.
Er kann die Menge von $C$ Kokosnüssen produzieren, welche er zum Preis von 1/Stück verkauft. Bei den Kokosnüssen handelt es sich um ein Numéraire Gut.[7]

$w$ bezeichnet den Lohnsatz pro Stunde für das Kokosnusssammeln.
$L$ stellt die getätigten Arbeitsstunden dar.
Dies ergibt in Kombination das Gewinnniveau $\Pi$ .

\Pi =C-wL

Stellt man die Gleichung nach $C$ um erhält man die Isogewinnlinie, der geometrische Ort aller Mengenkombinationen von Arbeit und Kokosnüssen, die der Unternehmung denselben Gewinn einbringen.

C=\Pi +wL

Der Gewinn wird an der Stelle maximiert, an der die Isogewinnlinie, die Produktionsfunktion tangiert. Dies bedeutet, dass das Grenzprodukt der Arbeit an dieser Stelle dem Lohnsatz entsprechen muss:
$GPA=w$ [7]

Konsument

Indifferenzkurve und Budgetgerade von Robinson nach Kokosnüssen und Arbeit

Man betrachtet Robinson Crusoe als Konsumenten. Er entscheidet zwischen Arbeit und Freizeit, welches somit seinen möglichen Konsum bestimmt.
Er kann sich aber auch entscheiden, überhaupt nicht zu arbeiten, da er gleichzeitig die Rolle des Aktionärs einnimmt und somit eine Grundausstattung von $\Pi$ zu Verfügung hat, welches er am Tag vorher produziert hat (in der Rolle des Produzenten).
Dies beruht auf der Tatsache, dass Arbeit für Robinson ein Ungut ist. Dies bedeutet, umso mehr er Arbeit konsumiert, senkt dies seinen Nutzen. Im Gegenteil dazu ist Kokosnuss ein Gut und erklärt somit die Steigung der Indifferenzkurve.

Durch die Grundausstattung am Punkt $(0,\Pi )$ und der Steigung $w$ erhält man die Budgetgerade von Crusoe. An dem Punkt, an dem die Indifferenzkurve die Budgetgerade tangiert, erhält man den optimalen Punkt. Hier entscheidet er, wie viel er arbeitet und wie viele Kokosnüsse er konsumieren will, unter der Annahme des gegebenen Lohnsatzes. Demzufolge muss die Grenzrate der Substitution gleich dem Lohnsatz entsprechen:

GRS=w

[7]

Gleichgewicht

Das Gleichgewicht mit dem Produktionsoptimum und dem Konsumoptimum

Im Gleichgewicht der Produzententheorie ist die Nachfrage nach Kokosnüssen gleich dem Angebot der Kokosnüssen. Im Gleichgewicht der Konsumententheorie entspricht die Nachfrage nach Arbeit gleich dem Angebot an Arbeit.

Fügt man beides zusammen, erhält man den Gleichgewichtspunkt, an dem die Steigung der Indifferenzkurve gleich der Steigung der Produktionsfunktion entspricht:

GRS_{F,K}=w

, wobei

F

für Freizeit steht und

K

für die Kokosnüsse

GPA=w

Zusammengefügt ergibt dies:

GRS_{F,K}=GPA

Das Ergebnis zusammengefügt bedeutet, dass ein Wettbewerbsgleichgewicht existieren kann. Dementsprechend gibt es Preise für Inputs und Outputs, die den Gewinn eines Unternehmens maximieren, sowie den Nutzen eines Individuums. An diesem Punkt sind somit Angebot und Nachfrage nach einem Gut gleich.[7]

Zwei-Personen-Wirtschaft

Transformationskurven von Robinson und Freitag nach den Gütern Kokosnüsse und Fische

Freitag strandet ebenfalls auf der einsamen Insel, dadurch kommt es ökonomisch gesehen zu wichtigen Veränderungen. Nun kann nicht nur Robinson Kokosnüsse oder Fische sammeln, sondern auch Freitag.
Freitag kann dies sogar wesentlich besser als Robinson. Beispielsweise sammelt er pro Woche maximal 60 Fische oder 60 Kokosnüsse.
Dies bedeutet auch, dass Freitag eine andere Produktionsmöglichkeitenkurve besitzt, welche sich oberhalb von Robinsons Transformationskurve befindet, da seine Produktivität bei beiden Gütern höher ist.
Bei solch einer Situation spricht man von einem absoluten Kostenvorteil.

Zudem weist die Transformationskurve eine flachere Steigung auf, das heißt auch die Opportunitätskosten der Beiden sind unterschiedlich.
Robinson und Freitag können sich nun auf jeweils eine Aufgabe spezialisieren, unter der Verwendung des Prinzips des komparativen Kostenvorteils. Dies besagt, dass jeder das Gut erstellen soll, das er relativ am billigsten produzieren kann.[2]

Die komparativen Kosten des Fischfanges:
Um bei gegebener Gesamtarbeitszeit einen Fisch mehr zu fangen, muss:

Robinson auf 2 Kokosnüsse verzichten
Freitag aber nur auf 1 Kokosnuss

Somit hat Freitag einen komparativen Vorteil beim Fischfang, gegenüber Robinson.

Die komparativen Kosten für eine Einheit Kokosnuss belaufen sich

bei Robinson auf ½ Fisch
bei Freitag auf 1 Fisch.

Somit hat Robinson einen komparativen Kostenvorteil beim Kokosnuss sammeln, gegenüber Freitag.

Daraus leitet man folgendes ab: Jeder sollte das produzieren, bei dem er einen komparativen Kostenvorteil besitzt. In Unserem Fall sollte Robinson Kokosnüsse sammeln und Freitag die Fische fangen.
Um den optimalen Punkt der von beiden gesammelten Güter zu bestimmen nimmt man an, dass Freitag bevor er auf der Insel strandete 30 Fische und 30 Kokosnüsse konsumierte und dieses Niveau beibehalten möchte. Zusammen mit dem Konsum von Robinson, welcher zehn Fische und 20 Kokosnüssen konsumierte, würden sie ohne Arbeitsteilung zusammen 40 Fische und 50 Kokosnüsse verzerren.

Konsum und Produktion von Robinson und Freitag ohne Arbeitsteilung:

	Robinson	Freitag	Summe
Kokosnüsse	20	30	50
Fische	10	30	40

Bei einer Arbeitsteilung nach dem Prinzip des komparativen Kostenvorteils sollte dieses Konsumniveau mindestens beibehalten werden.
Bei der Arbeitsteilung, spezialisiert sich Freitag auf den Fischfang. Um 40 Fische zu fangen, benötigt Freitag allerdings nur 2/3 seiner Wochenarbeitszeit, deshalb sammelt er noch zusätzlich 20 Kokosnüsse. Robinson spezialisiert sich auf das Sammeln von Kokosnüssen und erhält somit 40 Kokosnüsse.
Insgesamt haben die beiden zehn Kokosnüsse mehr gesammelt, als zuvor.

Produktion von Robinson und Freitag bei Arbeitsteilung:

	Robinson	Freitag	Summe
Kokosnüsse	40	20	60
Fische	0	40	40

Nun wird in dem Beispiel der Gewinn aus der Arbeitsteilung von 10 Kokosnüssen fair aufgeteilt. Beide besitzen nun 5 Kokosnüsse mehr.

Mit der verbundenen Arbeitsteilung können Robinson und Freitag miteinander handeln. Die zu handelnden Gütermengen ergeben sich aus der Differenz zwischen den produzierten und konsumierten Gütermengen.

Konsum von Robinson und Freitag bei Arbeitsteilung:

	Robinson	Freitag	Summe
Kokosnüsse	25	35	60
Fische	10	30	40

Handel zwischen Robinson und Freitag bei Arbeitsteilung:

Die Zusammengefügten Transformationskurven von Robinson und Freitag

	Robinson	Freitag
Kokosnüsse	Exportiert 15	Importiert 15
Fische	Importiert 10	Exportiert 10

Arbeiten beide zusammen in einer Zwei-Personen-Wirtschaft, ergeben sich die Eckpunkte A und B aus vollständiger Spezialisierung von Robinson und Freitag auf jeweils ein Gut. In Punkt A hätten die beiden ein maximalen Output von 100 Kokosnüssen und in Punkt B von 80 Fischen. In Punkt C würde Freitag 60 Fische fangen und Robinson 40 Kokosnüsse sammeln. Möchte die beiden mehr als 60 Fische verzerren, müsste auch Robinson Fische fangen und auf Kokosnüsse verzichten. „Die Steigung von Punkt A zu Punkt C gibt die komparativen Kosten der Fischproduktion von Freitag an (-1), die zwischen C und B, die komparativen Kosten von Robinson (-3).“[2]

Pareto-Effizienz

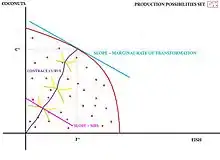
Pareto-effiziente Allokation in der Robinson-Crusoe-Wirtschaft mit der Transformationskurve und Egeworth-Diagramm an einem Punkt

Allgemein beschreibt die Pareto-effiziente Allokation, die Allokation bei der man nicht eine Einheit mehr von einem Gut erhält ohne dabei auf einen Teil des anderen Gutes zu verzichten. Zudem ist dies die Allokation, welches die Gewinne ausschöpft.
Es stehen für Robinson $c$ Einheiten Kokosnüsse und $f$ Einheiten Fische zur Verfügung. An jedem Punkt der Transformationskurve kann man ein Edgeworth-Diagramm zeichnen, um die möglichen Konsumbündel darzustellen.
Das Pareto-effiziente Bündel erhält man an dem Tangentialpunkt der Indifferenzkurven von Robinson und Freitag. Allgemein ist die Indifferenzkurve definiert als die Gütermengenkombination zwischen denen ein Haushalt indifferent ist. Die Grenzraten der Substitution sind jeweils an diesem Punkt gleich:

GRS_{R}=GRS_{F}

Auf der Kontraktkurve sind all diese Pareto-optimalen Lösungen abgetragen.
Zudem muss die Grenzrate der Substitution eines Konsumenten gleich der Grenzrate der Transformation sein, damit Pareto-Effizienz herrscht:

GRS_{R,F}=GRT_{R,F}

(Von jeweils Fischen und Kokosnüssen)[9][5]

Siehe auch

Literatur

Hal R. Varian: Grundzüge der Mikroökonomik. 7. Auflage. R. Oldenbourg Verlag, München/ Wien 2007, ISBN 978-3-486-58311-3.
Peter Bofinger: Grundzüge der Volkswirtschaftslehre. Eine Einführung in die Wissenschaft von Märkten. 3. Auflage. Pearson Studium, 2011, ISBN 978-3-8273-7354-0.
Ben Bernanke, Moore McDowell, Rodney Thom, Ivan Pastine, Robert Frank: Principle of Economics. 3. Auflage. Mc Graw Hill Education, 2012, ISBN 978-0-07-713273-6.

Weblinks

Einzelnachweise

Robinson Crusoe – Lag Blume – 2006 – Abgerufen am 19. Juni 2015.
Peter Bofinger: Grundzüge der Volkswirtschaftslehre – Eine Einführung in die Wissenschaft von Märkten. In: Pearson Education. Nr. 3, 2011, S. 32–39.
Peter Bofinger: Grundzüge der Volkswirtschaftslehre – Eine Einführung in die Wissenschaft von Märkten. In: Pearson Education. Nr. 3, 2011, S. 34.
Daniel McFadden 1975, 2003, Department of Economics, University of California – Abgerufen am 19. Juni 2015.
tau.ac.il Robinson Crusoe example - Yossi Spiegel - Abgerufen am 19. Juni 2015.
Peter Bofinger: Grundzüge der Volkswirtschaftslehre – Eine Einführung in die Wissenschaft von Märkten. In: Pearson Education. Nr. 3, 2011, S. 87–89.
Hal R. Varian: Grundzüge der Mikroökonomik. 7. Auflage. R. Oldenbourg Verlag, München/ Wien 2007, ISBN 978-3-486-58311-3, S. 702–707.
Hal R. Varian: Grundzüge der Mikroökonomik. 7. Auflage. R. Oldenbourg Verlag, München/ Wien 2007, ISBN 978-3-486-58311-3, S. 391–393.
Hal R. Varian: Grundzüge der Mikroökonomik. 7. Auflage. R. Oldenbourg Verlag, München/ Wien 2007, ISBN 978-3-486-58311-3, S. 716–718.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Robinson Crusoe – Lag Blume – 2006 – Abgerufen am 19. Juni 2015.

[Peter-2] Peter Bofinger: Grundzüge der Volkswirtschaftslehre – Eine Einführung in die Wissenschaft von Märkten. In: Pearson Education. Nr. 3, 2011, S. 32–39.

[3] Peter Bofinger: Grundzüge der Volkswirtschaftslehre – Eine Einführung in die Wissenschaft von Märkten. In: Pearson Education. Nr. 3, 2011, S. 34.

[4] Daniel McFadden 1975, 2003, Department of Economics, University of California – Abgerufen am 19. Juni 2015.

[Yossi-5] tau.ac.il Robinson Crusoe example - Yossi Spiegel - Abgerufen am 19. Juni 2015.

[6] Peter Bofinger: Grundzüge der Volkswirtschaftslehre – Eine Einführung in die Wissenschaft von Märkten. In: Pearson Education. Nr. 3, 2011, S. 87–89.

[Varian702-7] Hal R. Varian: Grundzüge der Mikroökonomik. 7. Auflage. R. Oldenbourg Verlag, München/ Wien 2007, ISBN 978-3-486-58311-3, S. 702–707.

[Varian391-8] Hal R. Varian: Grundzüge der Mikroökonomik. 7. Auflage. R. Oldenbourg Verlag, München/ Wien 2007, ISBN 978-3-486-58311-3, S. 391–393.

[9] Hal R. Varian: Grundzüge der Mikroökonomik. 7. Auflage. R. Oldenbourg Verlag, München/ Wien 2007, ISBN 978-3-486-58311-3, S. 716–718.