Realoptionsanalyse

Unter Realoptionen (englisch Real Options) versteht man die Handlungsspielräume des Managements von Unternehmen bei Investitionsentscheidungen. Die Realoptionsanalyse (englisch Real Option Valuation, ROV oder englisch Real Option Analysis, ROA) beschreibt als Teil der Investitionstheorie Optionspreismodelle zur Bewertung von Investitionen.

Die Kapitalwertmethode zur Beurteilung von Investitionen missachtet die unternehmerische Flexibilität bei zukünftigen Entscheidungen. Es wird unterstellt, dass die Unternehmen die projizierten Investitionen und Desinvestitionen auch tatsächlich durchführen werden. Es besteht jedoch die Chance, dass aufgrund unvorhergesehener Entwicklungen die angesetzten Investitionen an Wert verlieren und bzw. andere – noch nicht betrachtete Investitions- oder Desinvestitionsmöglichkeiten – werthaltig werden. Die Investitionsentscheidungen von Unternehmen sind bei der Betrachtung von Kapitalwerten demzufolge immer Entweder-oder-Entscheidungen: Bei positiven Kapitalwerten von Projekten investiert das Unternehmen bzw. bei negativen Kapitalwerten werden die Investitionen unterlassen. Die Möglichkeiten von Unternehmen, Investitionen in einem gewissen Rahmen hinauszuzögern, zu erweitern oder zu verkaufen werden bei den traditionellen Verfahren missachtet. Diese Handlungsspielräume bezeichnet man als Realoptionen. Diesen Handlungsmöglichkeiten (Realoptionen) kann mit verschiedenen Verfahren der Optionsbewertung (z. B. Binomialmodell, Black-Scholes-Modell) ein Wert zugewiesen werden. Die Realoptionswerte von Investitionen sind immer mindestens so hoch wie deren Kapitalwerte.

Geschichte

Der Begriff "Realoption" ist relativ neu und wurde 1977 von Stewart Myers von der MIT Sloan School of Management geprägt. Schon 1930 schrieb Irving Fisher ausdrücklich über "Optionen", die für einen Geschäftsinhaber verfügbar sind (The Theory of Interest, II.VIII). Die Beschreibung von Realoptionen wurde forciert durch die Entwicklung von Optionspreismodellen zur Bewertung von Finanzmarktoptionen, insbesondere durch das Modell von Black/Scholes (1973). Lenos Trigeorgis ist seit vielen Jahren ein führender Wissenschaftler auf diesem Gebiet, er veröffentlichte mehrere einflussreiche Bücher und wissenschaftliche Artikel. Weitere Wissenschaftler, die auf dem Gebiet der Realoptionen forschen, sind Michael Brennan, Eduardo Schwartz, Graham Davis, Gonzalo Cortazar, Han Smit, Avinash Dixit und Robert Pindyck (die beiden letzteren haben den einflussreichsten Text in diesem Fachgebiet verfasst). Das Konzept wurde von Michael J. Mauboussin, dem damaligen Chefstrategen der Credit Suisse First Boston in den USA, bei Praktikern populär gemacht. Er verwendet Realoptionen, um die Differenz zwischen Börsenkursen und den "inneren Werten" von Unternehmen zu erklären.

Eigenschaften von Investitionen

Die meisten Investitionsentscheidungen sind durch drei Eigenschaften gekennzeichnet:

Unsicherheit: Die zukünftigen Zahlungsströme von Investitionen sind unsicher. Unsicherheit entsteht dadurch, dass die für die Investitionsentscheidung relevanten Größen, wie Zinsen, Preise und Löhne, zum Teil unvorhersehbar sind.
Irreversibilität: Investitionsausgaben sind teilweise oder vollständig irreversibel. Mit anderen Worten: Die Auszahlungen für Investitionen sind zumindest anteilig „Sunk Costs“, d. h. sie können später nicht mehr rückgängig gemacht werden.
Flexibilität: Investitionen können hinausgezögert werden. In der Folge ist es möglich, neuere und bessere Informationen über den Wert von Investitionen abzuwarten.

Die traditionellen Bewertungskalküle auf Basis der Kapitalwertregel haben das Zusammenspiel von Unsicherheit, Irreversibilität und Flexibilität nicht hinreichend berücksichtigt. Aufgrund von Unsicherheit und Irreversibilität müssen Unternehmen die negativen Konsequenzen von Investitionsentscheidungen fürchten. Die Projektion zukünftiger Cashflows kann sich im Nachhinein als zu optimistisch herausstellen und die Irreversibilität nimmt den Unternehmen die Möglichkeit, die getroffenen Entscheidungen (vollständig) rückgängig zu machen. Die Flexibilität erlaubt jedoch, diesen Eigenschaften Rechnung zu tragen, eine verbesserte Informationslage abzuwarten und eine fundiertere Entscheidung zu treffen.

Analogien von Finanzmarkt- und Realoptionen

Eigenschaften von Calls und Puts

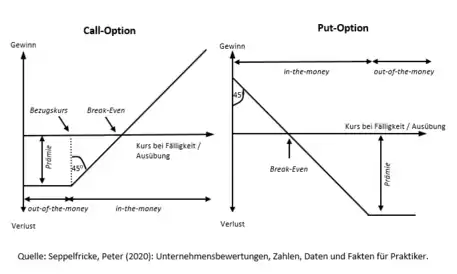
Bei einer Flexibilität im Timing von Investitionen lässt sich eine aufschlussreiche Analogie von realen Investitionen und Optionen auf Finanzmärkten erkennen. Eine Finanzoption ist eine vertragliche Vereinbarung, welche das Recht, jedoch nicht die Pflicht verbrieft, während der Laufzeit der Option einen bestimmten Vermögensgegenstand – den sogenannten Basiswert oder das Underlying – zu einem im Voraus vereinbarten Preis zu erwerben oder zu veräußern. Bei den Vermögensgegenständen kann es sich z. B. um Aktien, Währungen, Anleihen oder Indizes handeln. Kaufoptionen (Calls) gewähren das Recht zum Kauf, Verkaufsoptionen (Puts) das Recht zum Verkauf eines Vermögensgegenstandes. Die Basiswerte können zu einem festgelegten Zeitpunkt („europäische Option“: am Ende der Laufzeit) oder während einer Zeitspanne („amerikanische Option“: jederzeit während der Laufzeit) bezogen oder verkauft werden.

Die nebenstehende Abbildung verdeutlicht, dass die Risiko-Ertrags-Strukturen des Inhabers von Kauf- und Verkaufsoptionen asymmetrisch verteilt sind. Das bedeutet, dass die Gewinnmöglichkeiten nach oben offen sind (bei Verkaufsoptionen nahezu offen, da der Wert des Underlying nicht negativ werden kann), während der maximale Verlust auf den zu Beginn der Optionslaufzeit zu zahlenden Optionspreis begrenzt ist. Sofern die Option am Ende der Laufzeit „out of the money“ ist, lohnt sich die Ausübung nicht und die gezahlte Optionsprämie muss abgeschrieben werden. Falls der Ausübungspreis überschritten wird, ergibt es Sinn, die Option auszuüben. Der Gewinn aus der Ausübung entwickelt sich parallel zum Wert des Underlying. Allerdings wird der Break-even erst erreicht, wenn der Gewinn aus der Ausübung auch für die zuvor gezahlte Prämie kompensiert.

Die Analogie von Realoption und Finanzoption lässt sich leicht erkennen. Eine flexible Investition stellt eine Option für das Unternehmen dar, jetzt oder in Zukunft Geld auszugeben, um dafür in Zukunft Werte zu generieren. Die mit der Investition verbundenen Ausgaben entsprechen dem Ausübungskurs. Dabei ist zu beachten, dass die Option selbst nicht erworben wurde, sondern im Laufe der Jahre durch die Geschäftstätigkeit „verdient“ wurde. Der „Besitz“ der Option kann durch so unterschiedliche Aspekte wie den Ruf, die Marktposition oder auch das Eigentum an Patenten oder anderen Ressourcen begründet sein. Im Gegensatz zu Finanzmarktoptionen haben reale Investitionsmöglichkeiten keinen konkreten Auslaufzeitpunkt, sondern im Regelfall eine unendliche Laufzeit.

Beispiele: Die Digitalisierung führt zu radikalen Umbrüchen in vielen Branchen. Internet-Unternehmen wie Apple, Google, Facebook oder Amazon dringen in viele Märkte ein und gewinnen massiv Marktanteile. Diese Unternehmen haben sich auf ihren Plattformen viel Wissen über ihre Kunden, deren Bedürfnisse und Wünsche angeeignet. Sie verfügen über die wichtigste Währung in der digitalen Welt: eine ausgeprägte Kundenloyalität und eine hohe Aufmerksamkeit für neue Produkte. In der Folge haben diese Unternehmen vielfältige Möglichkeiten, ihre Fähigkeiten effizient und passgenau auch auf andere Dienstleistungen zu übertragen. Insbesondere die Marktführer bei digitalen Diensten verfügen deshalb über zahlreiche Realoptionen.

Die Tätigung der irreversiblen Investition entspricht der Ausübung. Mit der Ausübung wird der Nettokapitalwert (Net Present Value oder kurz NPV) der Option realisiert. Allerdings resultieren aus der Ausübung der Option auch Opportunitätskosten. Mit dem Entschluss, die Investition durchzuführen, vergibt der Investor die Möglichkeit, die Investitionsentscheidung später zu treffen und damit verbesserten Daten in Zukunft Rechnung zu tragen. Die Kapitalwertregel, als Basis aller Zahlungsstromverfahren, nach der so lange investiert werden soll, wie der Barwert einer Investition höher als deren Anschaffungskosten ist, muss deshalb modifiziert werden. In der Sprache der Optionspreistheorie berücksichtigt die NPV-Regel nur den inneren Wert einer Option. Man vernachlässigt dabei den sogenannten Zeitwert der Option, der entsteht, falls man durch Abwarten einen höheren Gewinn erzielen kann. Dieser Zeitwert ist durch die typische Asymmetrie einer Option bedingt: Falls der innere Wert der Anlage steigt, kann durch eine spätere Investitionsentscheidung ein entsprechender Gewinnzuwachs erzielt werden. Diesem Gewinnzuwachs steht aber im umgekehrten Fall kein entsprechendes Verlustpotenzial gegenüber, da bei einer Verminderung des inneren Wertes die Option nicht ausgeübt werden muss.

Die folgende Tabelle fasst die Parallelen von Finanzmarkt- und Realoptionen zusammen:

Analogien von Finanzmarkt- und Realoptionen
Finanzmarktoption	Realoption	Symbol
Tageskurs	Barwert der Einzahlungsüberschüsse (Kapitalwert)	V
Basispreis	Anschaffungskosten	I
Innerer Wert	Nettokapitalwert (NPV)	V – I
Laufzeit	Zeitraum für Handlungsspielraum	T
Volatilität	Streuung der Einzahlungsüberschüsse	σ
Dividende	Entgangene Rendite bei Nichtausübung der Realoption („Dividende“ der Investition)	ρ
Risikoloser Zins	Risikoloser Zins	r
Wert der Call-Option Wert der Put-Option	Wert der Investitionsmöglichkeit Wert der Desinvestitionsmöglichkeit	F(V) F(V)
Zeitwert	Wert des Wartens	F(V) – [V-I]
Ausübungsregel	Investitionsregel	V - I ≥ F(V) V ≥ I + F(V) Zeitwert ≤ 0

Jede Ausübung einer irreversiblen, aufschiebbaren Investition ist also mit der Aufgabe einer Option verbunden. Da Optionen Wahlrechte darstellen, deren Werte entsprechend immer positiv sind, muss die Kapitalwertregel modifiziert werden: Der Kapitalwert einer Investition V muss höher als seine Anschaffungskosten I sein, und zwar genau in der Höhe der Opportunitätskosten, die mit dem Gesamtwert der Option anzusetzen sind. Eine optimale Entscheidungsregel kann dann auf verschiedene Weise formuliert werden: Investiere genau dann, wenn

Der Net Present Value (Nettokapitalwert) der Investition NPV=V-I mindestens so groß ist wie seine Opportunitätskosten, die mit dem Gesamtwert der Option F(V) kalkuliert werden müssen,
der Present Value (Kapitalwert) aller zukünftigen Erträge V die gesamten Kosten abdeckt, die sich aus Anschaffungskosten I und Opportunitätskosten durch Verlust der Option F(V) zusammensetzen, oder
der Zeitwert der Option nicht größer als 0 ist.

Eigenschaften von Realoptionen

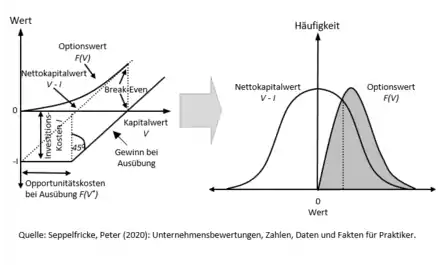
Die nebenstehende Abbildung verdeutlicht grafisch diese Zusammenhänge. Der Gewinn bei Ausübung ist der Wert, der bei Tätigung der Investition realisiert wird. Es wird zunächst der innere Wert (Nettokapitalwert) der Investition erzielt. Mit der Entscheidung, die Investition durchzuführen, entstehen jedoch auch Opportunitätskosten in Form der Aufgabe der Option: Dem Unternehmen wird die Möglichkeit genommen, weitere Informationen abzuwarten und die Entscheidung auf eine breitere Informationsgrundlage zu stellen. Die Investitionsentscheidung ist deshalb erst dann lohnend, wenn der Kapitalwert V sowohl für die Investitionskosten I als auch die Opportunitätskosten kompensiert. Die Opportunitätskosten sind mit dem Wert der Realoption bei Ausübung F(V*) anzusetzen.

Der Optionswert F(V) der noch nicht getätigten Investition kann nie negativ sein. Die Option stellt eine Wahlmöglichkeit dar, die nicht wahrgenommen werden muss. Mit zunehmendem Kapitalwert wird sich der Wert der Option dem Nettokapitalwert (V-I) annähern, da die Wahrscheinlichkeit der Ausübung dann gegen 1 geht. Der Break-even wird erreicht bzw. die Investition wird ausgeübt, wenn der innere Wert den Optionswert erreicht. Aufgrund der Asymmetrie der Option – dem Gewinnpotenzial steht auf der anderen Seite kein Verlustpotenzial gegenüber – hat der Optionswert in jeder Periode eine andere Häufigkeitsverteilung als der Nettokapitalwert NPV. Während der NPV in etwa um 0 normalverteilt streuen dürfte, weist der Optionswert eine rechtsschiefe Verteilung auf. Falls der Optionswert in einer Periode kleiner als der Nettokapitalwert ist, sollte die Investition getätigt werden.

Beispiel

Betrachtet sei ein Coffeeshop, der die Möglichkeit hat, irreversibel in neue Kaffeemaschinen zu investieren. Die Investitionskosten dieser Einheiten betragen I=8000,- €. Die Erlöse aus diesen Produkten werden dauerhaft auf 1000,- € pro Jahr geschätzt. Der relevante Diskontierungszins sei i=10%. Der Nettokapitalwert (NPV) der Investition beträgt:

$NPV=V-I=\sum \nolimits _{t=1}^{\infty }{\frac {1.000}{1.1^{t}}}-8.000=10.000-8.000=2.000$ €

Der Kapitalwert legt somit nahe zu investieren, da die Investition einen positiven Gegenwartswert besitzt bzw. der Barwert der Maschinen höher als seine Anschaffungskosten ist. In einer „Jetzt-oder-nie-Lage“ (und nur dann) wäre die Anwendung der NPV-Regel korrekt. Falls die Möglichkeit besteht, die Investition hinauszuzögern, werden bei der NPV-Regel allerdings die Opportunitätskosten der Investition missachtet. Es kann sich lohnen abzuwarten, ob die Preise in Zukunft fallen oder steigen.

Um das Beispiel einfach zu halten, betrage die Wahrscheinlichkeit 50 %, dass die Erlöse in der nächsten Periode auf 1.500,- € steigen und danach konstant bleiben. Auf der anderen Seite sei die Wahrscheinlichkeit, dass die Erlöse auf 500,- € fallen, ebenfalls 50 %. Diese Unsicherheit veranlasst das Unternehmen eine Periode abzuwarten und nur dann zu investieren, wenn die Erlöse steigen. Der Nettokapitalwert beträgt in diesem Falle:

$NPV=0,5*((\sum \nolimits _{t=1}^{\infty }{\frac {1.500}{1.1^{t}}}-8.000)/1.1)=3.181,82$ €

Der erwartete NPV ist also höher, wenn man die Investition ein Jahr lang aufschiebt und nur dann investiert, wenn der Preis in der Zwischenzeit gestiegen ist. Der Gesamtwert der Option beträgt 3.181,82 €. Er setzt sich zusammen aus dem inneren Wert der Investition in der heutigen Periode von 2.000,- € und dem Zeitwert der Option, der 1.181,82 € beträgt. Der Wert dieser zeitlichen Flexibilität ist dadurch entstanden, dass im Falle einer ungünstigen Ertragsentwicklung auf die Investition verzichtet werden kann, ohne dass „sunk costs“ anfallen, während man hingegen bei einer positiven Ertragsentwicklung einen höheren Barwert erzielen kann.

Bestimmung der Optionswerte

Stochastische Prozesse

Randbedingungen von Realoptionen

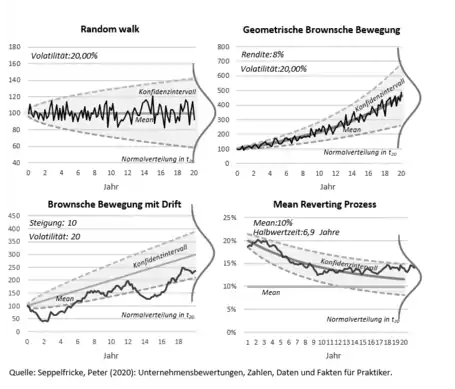
Zur Ermittlung von Optionswerten sind eine Vielzahl von Modellen entwickelt worden.[1] Für die Herleitung einer geschlossenen Lösung muss eine bestimmte Entwicklung der Kapitalwerte von Investitionen unterstellt werden. Es wird regelmäßig angenommen, dass die Kosten der Investition I fix sind und dass der Barwert einer Investition V, genauer die Summe aller zukünftigen diskontierten Einzahlungsüberschüsse, einer geometrischen Brown'schen Bewegung folgt:

$dV=\alpha Vdt+\sigma Vdz$ ,

wobei dz der Zuwachs eines Wiener-Prozesses, also „weißes Rauschen“ ist, und α die konstante prozentuale Drift von V beschreibt. Wertpapierkurse und Kapitalwerte werden in dynamischen Modellen häufig als geometrisch Brown’sche Bewegung modelliert. α stellt im Prozess die erwartete prozentuale Rendite einer Anlage dar. Da in der Praxis Wertpapierkurse oder Kapitalwerte aber schwanken, fügt der zweite Term dem Prozess die Unsicherheit hinzu. Dabei wird angenommen, dass die Volatilität (Standardabweichung) σ der Renditen in jeder Periode gleich ist.

Mit Hilfe von weiteren Eigenschaften von Realoptionen können geschlossene Formeln für den Wert der Optionen hergeleitet werden. Realoptionen weisen folgende Eigenschaften auf:

Amerikanische Optionen: Realoptionen sollen die Flexibilität bei Investitionsentscheidungen der Unternehmen modellieren. Naturgemäß muss es sich bei Realoptionen deshalb um amerikanische Optionen handeln, die eine jederzeitige Ausübung während der Laufzeit ermöglichen.
Dividenden: Es müssen bei Realoptionen Dividenden abgebildet werden, sonst würden auch amerikanische Optionen nie vor dem Ende der Laufzeit ausgeübt werden. Bei Ausübung einer Option wird immer der Zeitwert der Option aufgegeben. Dies lässt sich nur kompensieren, wenn im Gegenzug bei Ausübung der Realoption eine „Dividende“ bei den Investitionsprojekten realisiert werden kann. Bei realen Investitionsmöglichkeiten lassen sich die ausgeschütteten Free Cashflows einer Investition als „Dividende“ des Projektes interpretieren.
Nebenbedingungen von Optionen: Es lässt sich zeigen, dass der Wert einer Call-Option folgendermaßen begrenzt sein muss:
- F(V) ≥ 0: Der Wert einer Option kann nie < 0 sein. Eine Option stellt eine Wahlmöglichkeit dar, die nicht wahrgenommen werden muss. Falls der Wert des Projekts gegen Null geht, verliert die Option zu investieren ihren Wert: F(0)=0.
- F(V) ≥ V-I: Der Wert einer amerikanischen Option kann nie < V-I sein. Der Wert der Option muss mindestens dem Kapitalwert des Projekts abzüglich der Anschaffungskosten entsprechen. Ansonsten würde es bei „Ausübung“ der Option die Möglichkeit zur Arbitrage geben.
- Der Wert der Option muss sich dem Wert V-I annähern. Falls mit steigendem Nettokapitalwert des Projekts die Wahrscheinlichkeit der Ausübung gegen 1 geht, wird ein Gewinn in Höhe von V-I erzielt. Auch ohne Option steht dem Gewinnpotential auf der anderen Seite kein Verlustpotential gegenüber.

Stoppregel: Bei Realoptionen müssen Entscheidungsträger innerhalb der Laufzeit eine Entscheidung treffen, wann die Option ausgeübt wird. Für die stochastischen Prozesse müssen deshalb auch Stoppregeln definiert werden. Im Regelfall wird zu diesem Zweck ein Schwellenwert definiert. Bei Realoptionen wird die Option ausgeübt bzw. der Prozess gestoppt, wenn F = V-I erreicht wird. Den Zeitpunkt der Entscheidung nennt man Stoppzeitpunkt. Die Stoppzeit hängt von der Zufälligkeit des zugrundeliegenden stochastischen Prozesses ab und kann im Vorhinein nicht antizipiert werden. Der Stoppzeitpunkt ergibt sich also endogen und wird nicht vorgegeben. Man spricht in diesem Zusammenhang auch von einem freien Randwertproblem.
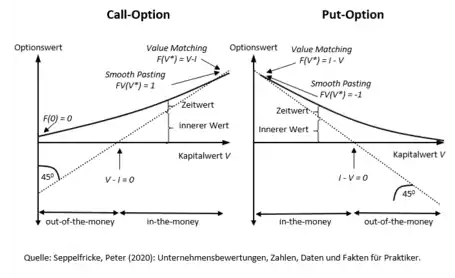
Randbedingungen von Realoptionen. Damit der Prozess aber gestoppt bzw. das freie Randwertproblem gelöst werden kann, müssen für Realoptionen typische Randbedingungen zur Anwendung kommen. Bezeichnet man mit V^* den Kapitalwert, bei dem der Stoppwert erreicht wird (Option wird ausgeübt), erhält man als Nebenbedingung: F(V^*) = V^*-I („Value Matching“). An dieser Stelle kann auch ein glattes Einlaufen der Option in den Nettokapitalwert V-I beobachtet werden (vgl. nebenstehende Abbildung). Die Steigungen der Optionspreisformel bzw. der Auszahlungsfunktion für den Nettokapitalwert sind bei diesem Schwellenwert identisch und es gilt δF/ δV = F_V(V) = 1 für einen Call bzw. δF/ δV = F_V(V) = -1 für einen Put. Diese Bedingungen nennt man auch „Smooth Pasting Condition“ oder „High Contact Condition“.[2]

Die nebenstehende Abbildung zeigt auf, wie sich der Gewinn- und Verlustbereich eines Calls bzw. Puts abhängig von der stochastischen Variablen V entwickelt. Bei einem Call mit bekannter Investitionsausgabe I kann höchstens ein Verlust in gleicher Höhe entstehen, falls das Projekt gar keinen Wert besitzt. Der Net Present Value (V-I) steigt linear mit dem Wert des Projekts V an.

Die Technik zur Bewertung von Optionen wurde erstmals in der bahnbrechenden Arbeit von Black/Scholes (1973) aufgezeigt. Sie haben erkannt. dass sich aus einer Investition und seinem Derivat ein risikoloses Portfolio konstruieren lässt, da es für beide eine identische Quelle der Unsicherheit gibt. Unter Verwendung der stochastischen Differenzierungsregeln von Itō Kiyoshi erhalten sie eine stochastische Differenzialgleichung die sich unter Verwendung der Randbedingungen von Optionen auflösen lässt. Dixit/Pindyck[3] greifen diese Ideen auf, beachten dabei jedoch die besonderen Eigenschaften von Realoptionen. Die erste Nebenbedingung, F(0)=0, legt nahe, folgende Lösungsform anzunehmen:

$F(V)=\alpha V^{\beta }$

wobei α und β Konstante sind, deren Werte von den Parametern σ², μ und ρ abhängen.Bezeichnet man mit V^* den Kapitalwert, bei dem es optimal ist zu investieren, kann man die Nebenbedingung: F(V^*)=V^*-I („Value Matching“) nutzen. Allerdings kann diese „freie Grenze“ V^* nicht ohne weitere Bedingung bestimmt werden. An dieser Stelle kommt die „Smooth Pasting Condition“ F_V(V^*) = 1 ins Spiel. Setzt man obige Formel in die Nebenbedingungen ein und formt um, erhält man:

$F(V)=aV^{\beta }$ , mit

$a=(V^{\ast }-I)/(V^{\ast })^{\beta }$ ,

$V^{\ast }={\frac {\beta }{\beta -1}}I$ ,

$\beta ={\frac {1}{2}}-{\frac {\mu -\delta }{\sigma ^{2}}}+\left[\left({\frac {\mu -\delta }{\sigma ^{2}}}-{\frac {1}{2}}\right)^{2}+{\frac {2\mu }{\sigma ^{2}}}\right]^{1/2}$ . ,

Mit Hilfe dieser Formel kann der Wert von Realoptionen bei einer unendlichen Laufzeit recht leicht ermittelt werden.

In der einschlägigen Literatur[4][5] findet man auch Absätze, bei denen das Binomialmodell von Cox/Ross/Rubinstein oder das Modell von Black/Scholes zur Bewertung von Realoptionen aufgegriffen wird. Die Anwendung dieser Modelle zur Bewertung von Realoptionen ist jedoch problematisch. Diese Modelle basieren auf Annahmen (europäische Optionen, vorgegebene Laufzeit, keine „Dividende“ der betrachteten Investitionsmöglichkeit), die bei Realoptionen nicht gegeben sind. Sie erweisen sich deshalb zur Bewertung von Realoptionen als ungenau.

Realoptionen von Kraftwerken

Mit der Neuregulierung der Energiemärkte kam es auf, die Flexibilitäten von Kraftwerken als Realoptionen, d. h. über Optionsmodelle, zu bewerten.

Zum Beispiel erzielt ein Gaskraftwerk Erlöse auf dem Strommarkt, denen ein Aufwand auf dem Gasmarkt gegenübersteht. Die Marge des Kraftwerks ergibt sich somit aus dem sogenannten Spark Spread, dem Unterschied zwischen Strompreis und dem mit 1 / Wirkungsgrad gewichteten Gaspreis.

Hinzu kommt jedoch ein Ergebnisbeitrag aus der disponiblen Verfügbarkeit (der Möglichkeit jederzeit zu produzieren oder auch nicht) und der Flexibilität (der Möglichkeit seine Fahrweise der Struktur der Marktpreise anzupassen) des Kraftwerks. Erzielt das Kraftwerk zunächst eine positive Marge aus dem Verkauf von Strom und Kauf von Gas, so wird der Kraftwerksbetreiber den zu erzeugenden Strom auf Termin verkaufen und das benötigte Gas einkaufen, um diese Marge abzusichern. Das heißt, er verkauft den Spark Spread. Stellt sich zu einem späteren Zeitpunkt heraus, dass sich die Produktion zu jetzt geltenden Marktpreisen nicht mehr lohnt, das heißt der Spark Spread ist jetzt negativ, so kann der Kraftwerksbetreiber entscheiden, doch nicht zu produzieren und stattdessen den Strom am Terminmarkt zurückzukaufen und das beschaffte Gas wieder zu verkaufen. Aus dieser Rückabwicklung resultiert ein Gewinn, da ein positiver Spark Spread verkauft und ein negativer zurückgekauft wurde. Der Gewinn resultiert aus der Realoption des Kraftwerksbetreibers, jederzeit seine Produktionsentscheidung zu revidieren. Je mehr Flexibilität das Kraftwerk hat, das heißt je mehr es seine Fahrweise in jeder Stunde den jederzeit sich ändernden Marktpreisen in jeder Stunde des Lieferjahres anpassen kann, desto höher der Wert der Realoption, der sich aus Ver- und Rückkaufen am Markt realisiert.[6]

Literatur

Martha Amram, Nalin Kulatilaka: Real Options: Managing Strategic Investment in an Uncertain World. Harvard Business School Press, Boston 1999, ISBN 978-0-87584-845-7 (Online).
Marion A. Brach: Real Options in Practice. Wiley, New York 2003, ISBN 978-0-471-44556-2.
Thomas E. Copeland, Vladimir Antikarov: Real Options: A Practitioner's Guide. Texere, New York 2001, ISBN 978-1-58799-028-1.
A. Dixit, R. Pindyck: Investment Under Uncertainty. Princeton University Press, Princeton 1994, ISBN 978-0-691-03410-2 (Online).
William T. Moore: Real Options and Option-embedded Securities. John Wiley & Sons, New York 2001, ISBN 978-0-471-21659-9.
T. J. Smit, Lenos Trigeorgis: Strategic Investment: Real Options and Games. Princeton University Press, Princeton 2004, ISBN 978-0-691-01039-7.
Trigeorgis, Lenos: Real Options: Managerial Flexibility and Strategy in Resource Allocation. The MIT Press, Cambridge 1996, ISBN 978-0-262-20102-5 (Online).
Reitz: Mathematik in der modernen Finanzwelt, 2011.
Seydel: Einführung in die numerische Berechnung von Finanzderivaten, 2. Auflage 2017, ISBN 3-662-50299-2.
Webel, Wied: Stochastische Prozesse – Eine Einführung für Statistiker und Datenwissenschaftler, 2. Auflage 2016.
Sandmann, Einführung in die Stochastik der Finanzmärkte, 1999.
Cox, Ross, Rubinstein: Option Pricing: A Simplified Approach, Journal of Financial Economics, 1979 S. 229–263.
Black/Scholes, The Pricing of Options and Corporate Liabilities, Journal of Political Economy, 1973 S. 637–654.
Müller: Realoptionsmodelle, S. 421 bis 434, in: Petersen/Zwirner (Hrsg.), Handbuch Unternehmensbewertung, 2. Auflage 2017.
Beckmann: Der Realoptionsansatz, S. 1583–1614, in: Peemöller (Hrsg.), Praxishandbuch der Unternehmensbewertung, 7. Auflage 2019.

Einzelnachweise

Thomas E. Copeland, Vladimir Antikarov: Real Options: A Practitioners Guide. Texere Publishing, 2003.
Seydel, Rüdiger: Einführung in die numerische Berechnung von Finanzderivaten : Computational Finance. ISBN 3-662-50299-2, S. 147 ff.
Pindyck, Robert S.: Investment under Uncertainty. Princeton University Press, 2008, ISBN 1-283-37955-4.
Müller: Realoptionsmodelle. In: Handbuch Unternehmensbewertung. 2. Auflage. 2017, S. 424–431.
Beckmann, Christoph: Der Realoptionsansatz in der Investitionsrechnung und Unternehmensbewertung. Utz, 2015, ISBN 978-3-8316-8089-4.
Hartung / Schlenker: Energiehandel in Europa - Vermarktung von Kraftwerken aus Handelssicht. Hrsg.: Zenke / Schäfer. C.H. Beck.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Thomas E. Copeland, Vladimir Antikarov: Real Options: A Practitioners Guide. Texere Publishing, 2003.

[2] Seydel, Rüdiger: Einführung in die numerische Berechnung von Finanzderivaten : Computational Finance. ISBN 3-662-50299-2, S. 147 ff.

[3] Pindyck, Robert S.: Investment under Uncertainty. Princeton University Press, 2008, ISBN 1-283-37955-4.

[4] Müller: Realoptionsmodelle. In: Handbuch Unternehmensbewertung. 2. Auflage. 2017, S. 424–431.

[5] Beckmann, Christoph: Der Realoptionsansatz in der Investitionsrechnung und Unternehmensbewertung. Utz, 2015, ISBN 978-3-8316-8089-4.

[6] Hartung / Schlenker: Energiehandel in Europa - Vermarktung von Kraftwerken aus Handelssicht. Hrsg.: Zenke / Schäfer. C.H. Beck.