Querprodukt
Das Querprodukt einer natürlichen Zahl ist – analog zur Quersumme – das Produkt ihrer Ziffernwerte. Das dezimale Querprodukt von 5496 ist beispielsweise 5·4·9·6 = 1080. Ebenso wie die Quersumme ist auch das Querprodukt abhängig vom verwendeten Zahlensystem. Im jeweiligen Zahlensystem entsprechen einstellige Zahlen ihrem eigenen Querprodukt.
Graphenverlauf
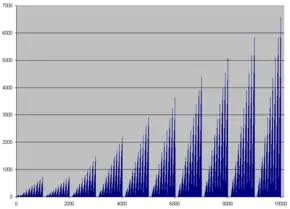
Der Graph der Querproduktfunktion, die jeder natürlichen Zahl n ihr Querprodukt q(n) zuordnet, besitzt einen charakteristischen Verlauf. Er besteht aus aufeinanderfolgenden Zacken, die immer höhere Spitzenwerte erreichen. Zwischen diesen Zacken fällt q(n) immer wieder auf 0; nämlich immer dann, wenn in n mindestens eine Ziffer 0 ist.
Dieses Verhalten tritt in jeder Zehnerpotenz auf – der Bereich 0 ≤ n ≤ 10 bildet ebenso eine Zacke wie 0 ≤ n ≤ 10.000. Auf diese Weise tritt im Graphen von q(n) Selbstähnlichkeit auf. Bei der Betrachtung einer Zehnerpotenz sind die ersten beiden Zacken immer gleich groß, die folgenden acht stellen das zwei-, drei-, vierfache usw. der ersten Zacken dar.
Der kleinste Funktionswert q(n) ist 0, eine Obergrenze existiert nicht.
Iteriertes Querprodukt
Erzeugt man eine Zahlenfolge, in der jede Zahl das Querprodukt ihres Vorgängers ist, so endet die Folge für jede mehrstellige Startzahl nach endlich vielen Schritten bei einer einstelligen Zahl. Dies liegt darin begründet, dass das Querprodukt einer mehrstelligen Zahl stets kleiner ist als die Zahl selbst.
3784 → 3·7·8·4 = 672 → 6·7·2 = 84 → 8·4 = 32 → 3·2 = 6
75664 → 7·5·6·6·4 = 5040 → 5·0·4·0 = 0
Die Anzahl der notwendigen Schritte wird als Beharrlichkeit[1] (engl. multiplicative persistence[2]) einer Zahl bezeichnet. Somit besitzt 3784 die Beharrlichkeit 4 und 75664 die Beharrlichkeit 2. Die einstellige Zahl, die man am Ende der Verkettung erhält, wird als multiplicative digital root (dt. „multiplikative Ziffernwurzel“) bezeichnet.
Für die folgenden Beharrlichkeiten sind im Dezimalsystem jeweils kleinste Startzahlen bekannt (Folge A003001 in OEIS). Eine Zahl mit der Beharrlichkeit 12 ist bislang nicht bekannt.[3]
| Beharrlichkeit von n | Kleinste Zahl n |
|---|---|
| 1 | 10 |
| 2 | 25 |
| 3 | 39 |
| 4 | 77 |
| 5 | 679 |
| 6 | 6 788 |
| 7 | 68 889 |
| 8 | 2 677 889 |
| 9 | 26 888 999 |
| 10 | 3 778 888 999 |
| 11 | 277 777 788 888 899 |
Literatur
- Eric Milou, Jav L. Schiffman: The Spirit of Discovery: The Digital Roots of Integers. In: Mathematics Teacher. Band 101 Nr. 5, Dezember 2007, S. 379–383.
- Richard K. Guy: Unsolved Problems in Number Theory. 3. Auflage. Springer-Verlag, 2004, ISBN 0-387-20860-7, S. 399 (Problem F25).
- N. J. A. Sloane: The Persistence of a Number (Memento vom 12. Januar 2011 im Internet Archive) In: Journal of Recreational Mathematics, Band 6, Nr. 2, 1973, S. 97–98.
- Clifford A. Pickover: Dr. Googols wundersame Welt der Zahlen. Heinrich Hugendubel Verlag, 2002, ISBN 3-423-34177-7, Kapitel 9: Hartnäckige Zahlen.
Weblinks
- Folge A007954 in OEIS (Querprodukte)
- Folge A003001 in OEIS (kleinste Startzahlen für Beharrlichkeiten)
- Eric W. Weisstein: Multiplicative Digital Root. In: MathWorld (englisch).
- Sloane’s conjecture on multiplicative digital root. In: PlanetMath.
Einzelnachweise
- Jens Fleckenstein, Walter Fricke, Boris Georgi: Excel – das Rätselbuch. Pearson Education 2007 ISBN 3-8272-4244-4, (eingeschränkte Online-Version (Google Books))
- Multiplicative digital root auf PlanetMath
- Pickover (s. Literatur)