Quantenmaschine

Die Quantenmaschine ist eine Maschine, deren Bewegungen sich durch die Quantenmechanik beschreiben lassen, während ihre Beschreibung im Rahmen der klassischen Mechanik nicht möglich ist. Die erste Quantenmaschine wurde im Jahr 2009 von Aaron D. O'Connell an der University of California, Santa Barbara im Rahmen seiner Promotion unter der Leitung von Andrew N. Cleland und John M. Martinis entwickelt.[1]

Photographie der von o'Connell entwickelten Quantenmaschine. Der mechanische Resonator befindet sich links von dem Koppelkondensator (kleines weißes Viereck), das Qubit rechts davon.

Andrew Cleland und John Martinis Quantenmaschine besteht aus einem ca. 40 µm großen mechanischen Oszillator, der elektrisch mit einem Qubit gekoppelt ist. Bei den Experimenten konnten verschiedene Quantenphänomene, wie z. B. die kontrollierte Erzeugung quantisierter Schwingungszustände (Phononen) und die Quantenverschränkung dieser Schwingungszustände mit dem Qubit beobachtet werden. Das US-Fachjournal Science hat die Quantenmaschine zum wissenschaftlichen Durchbruch des Jahres (englisch: „breakthrough of the year“) 2010 gekürt.[2]

Hintergrund

Die Idee, dass nicht nur Objekte in der Größenordnung von Molekülen, sondern auch makroskopische Objekte den Gesetzen der Quantenmechanik folgen könnten, stammt bereits aus den Anfängen der Quantenmechanik im frühen 20. Jahrhundert.[3] In der Größenordnung von Molekülen und darunter lieferten experimentelle Messungen bereits Ergebnisse, die der klassischen Physik widersprechen. Allerdings sind Quanteneffekte bei makroskopischen Objekten nicht leicht beobachtbar. Die Energiequanten makroskopischer Objekte sind so klein, dass Energieänderungen kontinuierlich aufzutreten scheinen.[4] Weiterhin werden durch unvermeidliche Dekohärenzeffekte die bei mikroskopischen Systemen typischen Interferenzeffekte sehr effizient unterdrückt.[5] Bei der von O'Connell entwickelten Quantenmaschine konnten diese Probleme durch ein optimiertes Resonatordesign und verschiedene weitere konstruktive Maßnahmen teilweise gelöst werden.

Aufbau der O'Connellschen Quantenmaschine

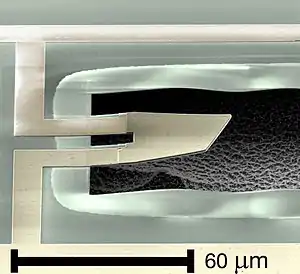
Elektronenmikroskopische Aufnahme des Herzstücks der Quantenmaschine, des Dünnfilm-Resonators. Die im Zentrum des Bildes sichtbare obere Elektrode verdeckt den Blick auf die piezoelektrische Schicht und auf die untere Elektrode.

Der Oszillator der von O'Connell entwickelten Quantenmaschine war ein in Dünnschichttechnologie hergestelltes Piezoelement aus Aluminiumnitrid mit einem Durchmesser von 40 µm und einer Dicke von 330 nm. Dieser Durchmesser entspricht ungefähr dem Durchmesser dünnen menschlichen Flaumhaars, der Oszillator der Quantenmaschine war mit bloßem Auge gerade noch erkennbar. Durch Anlegen einer elektrischen Wechselspannung zwischen den Elektroden konnten Dehnungsschwingungen des Piezoelements angeregt werden, wobei die Resonanzfrequenz dieser Schwingungsmode bei etwa 6 GHz lag. Durch Abkühlen des Oszillators auf eine Temperatur von 25 mK konnten thermische Einflüsse auf das Experiment, insbesondere die thermische Anregung von Schwingungsquanten weitgehend unterdrückt werden. Das Piezoelement war mit einem Josephson-Kontakt kapazitiv gekoppelt, der als Qubit verwendet wurde. Die Kopplung zwischen Resonator und Qubit konnte durch Steuerung der Josephson-Frequenz des Josephson-Kontakts und durch Einkoppeln von Mikrowellenpulsen in den Koppelkondensator beeinflusst werden.

Quanteneffekte

An der Quantenmaschine konnten verschiedene Quanteneffekte nachgewiesen werden.

Zunächst bestimmten die Forscher die mittlere Anzahl thermisch angeregter Schwingungsquanten (Phononen) des Resonators. Hierbei wurde das Qubit als Sonde verwendet, welches in seinem Grundzustand $|g\rangle$ präpariert wurde. Aus der geringen Wahrscheinlichkeit für Anregungsereignisse des Qubits konnte abgeleitet werden, dass die mittlere Phononenzahl bei 0,07 lag, d. h. der Resonator befand sich mit einer Wahrscheinlichkeit von 93 % in seinem quantenmechanischen Grundzustand $|0\rangle$ .

In einem nächsten Schritt wurden kontrolliert einzelne Schwingungsquanten des Resonators angeregt. Bei diesem Experiment wurde zunächst das Qubit in seinen angeregten Zustand $|e\rangle$ gebracht, woraufhin ein periodischer Wechsel (Rabi-Oszillationen) des Energiequants vom Qubit zum Resonator und zurück beobachtet wurde. Der Resonator und das Qubit befanden sich also in einem verschränkten Zustand. Die Lebensdauer der Rabi-Oszillation war hauptsächlich durch die Dämpfung des Resonators begrenzt, die Zerfallszeit (genauer: die $T_{1}$ -Relaxationzeit) lag bei 6,1 ps. Aufgrund dieser kurzen Lebensdauer war es nicht möglich, eine vollständige Bestimmung des quantenmechanischen Zustands durch eine Zustandstomographie durchzuführen.

Rezeption

Die Experimente der Arbeitsgruppe aus Santa Barbara wurden in der Zeitschrift Nature veröffentlicht und von der Zeitschrift Science zum Durchbruch des Jahres 2010 gekürt.[1][2] Nach Einschätzung des Science-Autors Cho eröffnen die Ergebnisse unter anderem neue Möglichkeiten zur Entwicklung ultrasensitiver Kraftsensoren und zur Erzeugung von Quantenzuständen von Licht. Weitere Anwendungen sieht Cho in der Grundlagenforschung in der Durchführung von Tests der Quantenmechanik bei Anwendung auf makroskopische Objekte.

Einzelnachweise

A. D. O’Connell, M. Hofheinz, M. Ansmann, R. C. Bialczak, M. Lenander, E. Lucero, M. Neeley, D. Sank, H. Wang, M. Weides, J. Wenner, J. M. Martinis, and A. N. Cleland, Quantum ground state and single-phonon control of a mechanical resonator, Nature, Vol. 464, April 2010, S. 697–703, doi:10.1038/nature08967.
Adrian Cho, Breakthrough of the Year: The First Quantum Machine, Science, Vol. 330, Nr. 6011, 2010, S. 1604, doi:10.1126/science.330.6011.1604
E. Schrödinger, Die gegenwärtige Situation in der Quantenmechanik, Die Naturwissenschaften, Bd. 23, 1935, doi:10.1007/BF01491891 (Teil 1), doi:10.1007/BF01491914 (Teil 2), doi:10.1007/BF01491987 (Teil 3)
Beispielsweise beträgt ein Energiequantum der Schwingung eines Pendels mit einer Schwingungsfrequenz von 1 Hertz etwa $6\cdot 10^{-34}\,\mathrm {J}$ .
W. H. Zurek, Decoherence, Einselection, and the Quantum Origins of the Classical, Reviews of Modern Physics, Vol. 75, 2003, S. 715–765.

Literatur

Marcelo Alonso, Edward J. Finn: Quantenphysik und Statistische Physik. 2005. ISBN 978-3-486-57762-4
Stephen Gasiorowicz: Quantenphysik. 9. Auflage 2005. ISBN 978-3-486-27489-9

Weblinks

Ausführlicher Artikel in dem von der DPG betriebenen online-Magazin pro-Physik
Aaron O'Connell: Making sense of a visible quantum object Video eines TED-Vortrags von Aaron O'Connell über seine Quantenmaschine (englisch)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[oConnell_Nature_2010-1] A. D. O’Connell, M. Hofheinz, M. Ansmann, R. C. Bialczak, M. Lenander, E. Lucero, M. Neeley, D. Sank, H. Wang, M. Weides, J. Wenner, J. M. Martinis, and A. N. Cleland, Quantum ground state and single-phonon control of a mechanical resonator, Nature, Vol. 464, April 2010, S. 697–703, doi:10.1038/nature08967.

[Cho_Science_2010-2] Adrian Cho, Breakthrough of the Year: The First Quantum Machine, Science, Vol. 330, Nr. 6011, 2010, S. 1604, doi:10.1126/science.330.6011.1604

[3] E. Schrödinger, Die gegenwärtige Situation in der Quantenmechanik, Die Naturwissenschaften, Bd. 23, 1935, doi:10.1007/BF01491891 (Teil 1), doi:10.1007/BF01491914 (Teil 2), doi:10.1007/BF01491987 (Teil 3)

[GrößenordnungEnergiequanten-4] Beispielsweise beträgt ein Energiequantum der Schwingung eines Pendels mit einer Schwingungsfrequenz von 1 Hertz etwa $6\cdot 10^{-34}\,\mathrm {J}$ .

[Zurek_Review_2003-5] W. H. Zurek, Decoherence, Einselection, and the Quantum Origins of the Classical, Reviews of Modern Physics, Vol. 75, 2003, S. 715–765.