Quadratrix von Tschirnhaus

Die Quadratrix von Tschirnhaus, benannt nach Ehrenfried Walther von Tschirnhaus (1651–1708), ist eine gestauchte Sinuskurve, mit deren Hilfe sich eine Quadratur des Kreises, d. h. die Umwandlung eines Kreises in ein exakt flächengleiches Quadrat durch eine Konstruktion mit Zirkel und Lineal, durchführen lässt. Aufgrund dieser Eigenschaft wird sie als Quadratrix bezeichnet. Da sie sich außerdem zur Dreiteilung des Winkels verwenden lässt, ist sie auch eine Trisektrix.

Tschirnhaus-Qudratrix (rot), Quadratrix des Hippias (gestrichelt)

Definition

Die Quadratrix von Tschirnhaus wird ähnlich wie die Quadratrix des Hippias über zwei gleichförmige Bewegungen definiert und es wird daher vermutet, dass Tschirnhaus bei seiner Konstruktion von der des Hippias inspiriert wurde.

In einem Quadrat ABCD bewegt sich ein Punkt F mit einer konstanten Geschwindigkeit auf der Seite AD von D nach A. Gleichzeitig bewegt sich ein weiterer Punkt E ebenfalls mit einer konstanten Geschwindigkeit auf dem Viertelkreis um A von D nach B. Dabei werden die beiden konstanten Geschwindigkeiten so gewählt, dass F und E zur gleichen Zeit an ihren Zielen A und B ankommen. Durch den Punkt F wird nun eine Parallele zur Seite AB gezogen und im Punkt E das Lot auf die Seite AB gefällt. Parallele und das Lot schneiden sich in einem Punkt S, der mit fortschreitender Bewegung von E und F von D nach B wandert. Die Quadratrix von Tschirnhaus ist nun definiert als die Ortskurve des Punktes S.

Platziert man das Quadrat ABCD so im Koordinatensysten, dass der Punkt D im Ursprung und die Seite AD auf der x-Achse liegt, dann lässt sich die Quadratrix wie folgt anhand einer gestauchten Sinusfunktion beschreiben:

f(x)=r\sin \left({\frac {\pi x}{2r}}\right)

Hierbei ist r der Radius des Viertelkreises beziehungsweise die Seitenlänge des Quadrats.

Winkelteilung

Dreiteilung eines Winkels,

\alpha =\beta =\gamma

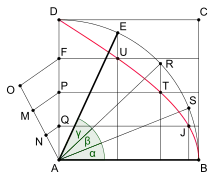
Aufgrund der Konstruktion der Quadratrix über gleichförmige Bewegungen entspricht das Verhältnis der Länge eines Streckenabschnitts auf der Quadratseite AD zu der Länge der Gesamtseite dem Verhältnis der Länge des entsprechenden Abschnittes auf dem Kreisbogen zur Länge des Viertelkreises. Letzteres Verhältnis entspricht aber dem der zu den Kreisbögen gehörigen Winkel, somit erhält man über die Quadratrix zu einer Teilung einer Strecke auf der Quadratseite auch eine entsprechende Teilung der zugehörigen Winkel. Die ermöglicht damit das folgende Verfahren zur Teilung eines Winkels in n gleiche Teile.

Zu einem gegebenen Winkel BAE errichtet man über seinem Schenkel AB das Quadrat ABCD und die zugehörige Quadratrix. Der Viertelkreis um A mit Radius |AB| schneidet den anderen Schenkel des Winkels in E. Von E fällt man nun das Lot (Senkrechte) auf den Winkelschenkel AB und das Lot schneidet die Quadratrix in U. Durch U zeichnet man eine Parallele zum Schenkel AB, der die Quadratseite AD in F schneidet. Die Unterteilung der Strecke AF in n gleiche Teile liefert dann über die Quadratrix eine Unterteilung des Winkels in n gleiche Teile, indem man durch die Teilpunkte der Strecke AF weitere Parallelen zum Schenkel AB zeichnet. In deren Schnittpunkten mit der Quadratrix errichtet man Lote zu AB, deren Schnittpunkte mit dem Viertelkreis schließlich die Teilung des Winkels liefern. Die Unterteilung der Strecke AF selbst mit Zirkel und Lineal ist aufgrund des Strahlensatzes möglich (siehe Zeichnung und Teilung einer Strecke mit Zirkel und Lineal in einem vorgegebenen Verhältnis).

Kreisquadratur

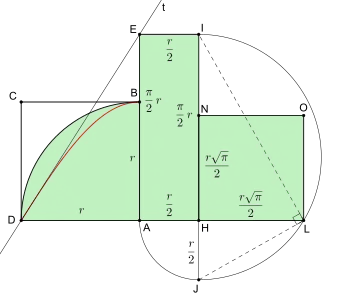
Kreisquadratur mithilfe der Quadratrix und ihrer Tangente

Setzt man voraus, dass man neben der Quadratrix selbst auch ihre Tangente zur Verfügung hat, das heißt das Konstruktionsgerät für die Quadratrix liefert zumindest in deren Endpunkten B und D auch die zugehörige Tangente, dann schneidet die Tangente durch D die Verlängerung der Seite AB in E mit $|AE|={\tfrac {\pi }{2}}|AB|$ . Mit AE lässt sich nun ein Rechteck konstruieren, dessen Fläche dem Viertelkreis entspricht, und dieses Rechteck lässt sich mit Hilfe des Höhensatzes von Euklid oder des Kathetensatzes in ein flächengleiches Quadrat umwandeln (siehe Zeichnung).

Literatur

John Martin Frederick Wright: An Algebraic System of Conic Sections, and other Curves. Black and Armstrong, 1836, S. 206-208
Nikolaus Fialkowski: Theilung des Winkels und des Kreises, oder: Bi-, Tri-, Quadri- und Polysection jedes beliebigen Winkels in 72 neuen Methoden.Gerold, Wien 1860, S. 208-211
A.B. Ivanov: Quadratrix. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 978-1-55608-010-4 (englisch, online).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.