Problem der monohedralen, aperiodischen Parkettierung
Das Problem der monohedralen, aperiodischen Parkettierung ist ein offenes mathematisches Problem aus der Diskreten Geometrie und fragt nach der Existenz einer einzelnen Kachel (Protokachel), welche die Ebene ohne zusätzliche Regeln, die das korrekte Zusammenfügen sicherstellen, ausschließlich nichtperiodisch parkettieren kann. Das bekannteste Beispiel einer nichtperiodischen Parkettierung der Ebene ist die sogenannte Penrose-Parkettierung, welche allerdings einen Satz aus mindestens zwei verschiedenen Protokacheln benötigt (siehe Abbildung). Für eine aperiodische Monokachel hat sich im Englischen der Begriff „Einstein“ etabliert. Dieses Wortspiel mit den Wörtern „Ein“ und „Stein“, stellvertretend für „Eine (einzelne) Kachel“, wird en:Ludwig Danzer zugeschrieben. Die Assoziation zu dem Physiker Albert Einstein ist dabei gewollt und der eigentliche Witz des Wortspiels, auch wenn das Problem selbst nichts mit der Person und ihrer wissenschaftlichen Arbeit verbindet. Im deutschen Sprachgebrauch hat sich der Begriff Einstein-Problem noch nicht durchgesetzt. Das Problem kann auch als natürliche Erweiterung des zweiten Teils von Hilberts achtzehntem Problem angesehen werden, in dem nach einem einzelnen Polyeder gefragt wird, das den dreidimensionalen euklidischen Raum lückenlos füllt, aber keine Raumfüllung durch dieses Polyeder isohedral ist.[1] Solche anisohedralen Polyeder wurden erstmals 1928 von Karl Reinhardt vorgestellt.[2] 1932 fand Heinrich Heesch eine solche Lösung auch für die Ebene.
Lösungsansätze


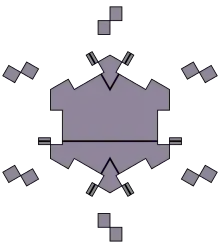
Nach heutigem Kenntnisstand gibt es keine Gründe, die für oder gegen die Existenz mindestens einer aperiodischen Monokachel sprechen. Auch ist völlig unklar, wie eine solche Kachel aussehen könnte. Die bis heute besten Approximationen für das Problem benötigen entweder zusätzliche Parkettierungsregeln wie Dekorationen, sind unzusammenhängend, oder es müssen minimale Überlappungen bzw. Lücken im Parkett in Kauf genommen werden.
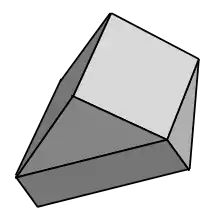
1988 entdeckte Peter Schmitt ein Polyeder zur nichtperiodischen lückenlosen Parkettierung des dreidimensionalen euklidischen Raums. Während keine dieser Raumfüllungen eine Parallelverschiebung als Symmetrie zulässt, weisen jedoch einige eine Schiefsymmetrie auf, die als eine Kombination aus einer Parallelverschiebung und einer Rotation über ein irrationales Vielfaches der Kreiszahl (Pi) verstanden werden kann, sodass keine Anzahl von wiederholten Operationen jemals eine reine Parallelverschiebung ergibt. Diese Konstruktion wurde später von John Horton Conway und Ludwig Danzer zu einem konvexen aperiodischen Raumfüller, der Schmitt-Conway-Danzer-Kachel, erweitert (siehe Abbildung). Das Vorhandensein der Schiefsymmetrie führte zu einer Neubewertung der Anforderungen an die Nichtperiodizität.[3] Chaim Goodman-Strauss schlug vor, eine Kachelung als stark aperiodisch zu bezeichnen, wenn sie keine unendliche zyklische Gruppe euklidischer Transformationen als Symmetrien zulässt, und nur Kachelsätze, die eine starke Aperiodizität erzwingen, als stark aperiodisch zu bezeichnen, während andere Sätze als schwach aperiodisch zu bezeichnen sind.[4]
Im Jahr 1996 konstruierte Petra Gummelt eine dekorierte zehneckige Protokachel und zeigte, dass diese die Ebene zwingend nichtperiodisch parkettieren kann, wenn zwei Arten von Überlappungen zwischen Kachelpaaren zugelassen werden (siehe Abbildung).[5] Wegen der unzulässigen Überlappungsregeln löst die Gummelt-Kachel das Problem nicht.
Ein weiterer Lösungsansatz aus dem Jahr 2010 stammt von Joshua Socolar und Joan Taylor.[6] Die Parkettierung der euklidischen Ebene mit der Socolar-Taylor-Kachel erfordert Zusammenfügungsregeln, welche die relative Ausrichtung von zwei Kacheln einschränken und auf gezeichnete Dekorationen der Kacheln verweisen. Diese Regeln gelten für Paare nicht benachbarter Kacheln. Alternativ kann eine nicht dekorierte, jedoch unzusammenhängende Kachel ohne Zusammenfügungsregeln erstellt werden (siehe Abbildung). Diese Variante der Socolar-Taylor-Kachel ist aus drei verschiedenen Protokacheln in fester Anordnung zusammengesetzt (insgesamt 19) und ist damit nach Definition keine abgeschlossene topologische Scheibe mehr. Diese Konstruktion kann wiederum auf ein raumfüllendes, zusammenhängendes Polyeder ohne Zusammenfügungsregeln erweitert werden. Die damit möglichen Raumfüllungen sind allerdings in einer Richtung periodisch, weshalb die dreidimensionale Socolar-Taylor-Kachel nur schwach aperiodisch ist.
Einzelnachweise
- Marjorie Senechal: Quasicrystals and Geometry. paperback ed. with corrections. Cambridge University Press, 1996, ISBN 0-521-57541-9, S. 22–24.
- Karl Reinhardt Zur Zerlegung der euklidischen Räume in kongruente Polytope in: Sitzungsberichte der Preussischen Akademie der Wissenschaften. 1928, S. 150–155.
- Charles Radin: Aperiodic tilings in higher dimensions. In: American Mathematical Society (Hrsg.): Proceedings of the American Mathematical Society. 123, Nr. 11, 1995, S. 3543–3548. doi:10.2307/2161105.
- Chaim Goodman-Strauss: Open Questions in Tiling. 10. Januar 2000. Archiviert vom Original am 18. April 2007. Abgerufen am 24. März 2007.
- Petra Gummelt: Penrose Tilings as Coverings of Congruent Decagons. In: Geometriae Dedicata. 62, Nr. 1, 1996, S. 1–17. doi:10.1007/BF00239998.
- Joshua E. S. Socolar, Joan M. Taylor: An Aperiodic Hexagonal Tile. In: Journal of Combinatorial Theory, Series A. 118, Nr. 8, 2011, S. 2207–2231. arxiv:1003.4279. doi:10.1016/j.jcta.2011.05.001.