Physik des Segelns
Die Physik des Segelns (auch Theorie des Segelns) erklärt die physikalischen Grundlagen der Tatsache, dass sich ein Segelfahrzeug unter Ausnutzung des Windes fortbewegen kann. Die Betrachtungen erlauben es unter anderem zu verstehen, weshalb Segelfahrzeuge auch gegen den Wind fahren können oder schneller segeln können als der Wind weht.
Eine Einführung in das Thema gehört zu jeder Segelausbildung.
Definitionen und Begriffe
.jpg.webp)
Wahrer und scheinbarer Wind
Jedes segelnde Schiff bewegt sich mit der Kraft des Windes. Als wahrer Wind wird in der Schifffahrt der tatsächlich an einem gegebenen Ort wehende Wind mit Richtung und Stärke bezeichnet. Der wahre Wind kann nur durch ortsfeste Einrichtungen gemessen werden. Der scheinbare Wind ist der Wind, der an Bord eines sich in Bewegung befindlichen Schiffes weht. Er unterscheidet sich vom wahren Wind und ergibt sich durch eine Vektoraddition des wahren Windes mit dem Fahrtwind des Schiffes. Anhand des nebenstehenden Bildes kann man sehen, dass die Stärke und Richtung des scheinbaren Windes nicht nur von der Stärke des wahren Windes, sondern wesentlich auch von der Schiffsgeschwindigkeit und der Fahrtrichtung des Schiffes relativ zur Windrichtung (Kurs zum Wind) abhängt.
Kurse zum Wind
Als Kurs zum Wind bezeichnet man den Kurs (Richtung, in die das Schiff fährt) relativ zur Windrichtung. Es werden im Wesentlichen folgende Situationen unterschieden:
- Am Wind: Das Schiff läuft schräg gegen den Wind. Weil hier Fahrtwind und wahrer Wind aus fast der gleichen Richtung kommen, ist die Geschwindigkeit des scheinbaren Windes am größten. Der kleinstmögliche Winkel zum Wind hängt von der Konstruktion des Schiffes ab.
- Halbwind: Das Schiff fährt ungefähr quer zur Richtung des scheinbaren (bzw. wahren)[1] Windes.
- Raumschots: Der Wind weht „schräg von hinten“ auf das Schiff.
- Vor dem Wind: Der Wind weht genau von achtern (von hinten) auf das Schiff. Hier ist die Geschwindigkeit des scheinbaren Windes am geringsten.
- Im Wind: Der Wind weht genau von vorne auf das Schiff. In diese Richtung kann ein normales Segelschiff nicht fahren.
Abhängig vom Kurs zum Wind wählt der Segler die Stellung der Segel. Als Faustregel gilt: Der Baum halbiert den Winkel zwischen Mittschiffslinie und Windeinfallswinkel. Auf Amwindkursen sind die Segel und Schoten sehr dicht geholt, auf Vorwindkursen stehen die Segel fast querschiffs. Durch das Trimmen der Segel werden die Segel genau auf die vorherrschenden Wind- und Seegangsverhältnisse eingestellt.
Aerodynamik des Segelns
Antrieb eines Segelschiffes
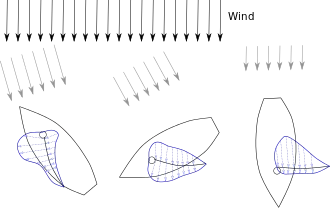
_and_down_wind_(left).jpg.webp)
Ein Segelschiff wird durch zwei Effekte vorangetrieben: durch Winddruck auf das Segel und durch Luftströmung um das Segel, die durch Unterdruck am Segel zieht. In der Praxis überlagern sich meistens beide Effekte, wobei je nach Kurs zum Wind der eine oder der andere Teil überwiegt. Beim fahrenden Schiff ist die Gegenkraft zum Vortrieb im Wesentlichen der Wasserwiderstand, der auf den Schiffsrumpf wirkt. Der hauptsächliche Vortrieb entsteht durch die Übertragung des Winddruckes auf den oder die segelführenden Masten und Schoten, und die Kraft überträgt sich wiederum auf den Schiffsrumpf. Der Rumpf wird quasi „mitgezogen“.
Das vom Wind angeströmte Segel nimmt eine gewölbte Form (Bauch) an und entwickelt eine Kraft, die proportional zum Produkt aus der Segelfläche und dem Quadrat der Windgeschwindigkeit ist. Die Kraft wirkt senkrecht zur Fläche des Segels in Richtung Lee. Einfluss auf die Größe der Kraft hat neben Form und Größe des Segels und der Windgeschwindigkeit auch der Anströmwinkel des Windes auf das Segel. Je nach Anströmwinkel überwiegt entweder die Komponente Antrieb durch Widerstand oder die Komponente Antrieb durch Auftrieb (Diagramm 1).
Winddruck auf das Segel
Trifft der Wind von hinten (auf Vorwindkurs) oder von schräg hinten (auf Raumwindkurs) auf das Segelschiff, erfolgt der Antrieb des Segelschiffes durch den Widerstand, den die Segel dem Wind entgegensetzen. Die Luftströmung wird dabei unterbrochen und der Wind versucht, den Widerstand „wegzuschieben“. Diese Art des Vortriebs wird am günstigsten durch die früher auf Großseglern verwendeten Rahsegel genutzt. Auch die Großsegler fuhren auf Raumwindkurs schneller als auf Vorwindkurs, da bei Letzterem die meisten Segel in den Windschatten der hintersten Segel geraten. Moderne Segelschiffe mit Schratsegeln sind nicht besonders gut für den Antrieb durch Widerstand geeignet, da es den Schratsegeln besonders im oberen, wirksameren Bereich an Segelfläche fehlt. Um diese Nachteile auszugleichen, werden im Kursbereich Vor dem Wind bis Halber Wind zusätzlich große, bauchige Segel wie Spinnaker oder Gennaker eingesetzt.
Windströmung am Segel (Tragflächeneffekt)
Segelschiffe sind in der Lage, schräg gegen den Wind zu segeln und aufzukreuzen. Dadurch können Ziele erreicht werden, die in Windrichtung liegen. Dabei haben Schratsegel die größte Effizienz. Segel verhalten sich strömungstechnisch ähnlich dem Tragflügel eines Flugzeuges. Die Wölbung (der Bauch) des Segels bewirkt komplexe aerodynamische Abläufe und Strömungen rund um das Segel. Die unterschiedlichen Strömungsgeschwindigkeiten auf Luv- und Leeseite der laminaren Strömung am Segel vorbei führen zu Druckunterschieden, die sich zu einem Gesamtvektor aufaddieren, der bezogen auf die Tragfläche, also das Segel, nach Lee und vorwärts zeigt. Dazu ist eine Kraft erforderlich. Diese Kraft wird zum Teil in Vortrieb und zum anderen Teil in Abdrift nach Lee und – durch den Widerstand des Kiels oder Schwertes unter Wasser – in Krängung (Schräglage des Schiffes) umgesetzt. Da die Segel nur bei Umströmung Auftrieb (bzw. Vortrieb) liefern, spricht man von dynamischem Auftrieb.


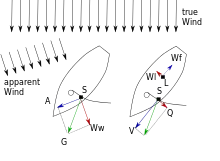
Das nebenstehende Diagramm 2 erläutert die Kräfte, die an einem Boot wirken, das auf Amwindkurs segelt. Die linke Darstellung zeigt die Kraft G, die der Wind auf das Segel ausübt. Die Windkraft kann in Auftrieb A und Luftwiderstand Ww zerlegt werden. Der Auftrieb ist bei optimaler Anströmung des Segels ungefähr fünfmal so groß wie der Luftwiderstand. Durch die Form des Bootsrumpfes und den Lateralplan wird die Querbewegung reduziert und der Vortrieb optimiert (rechte Darstellung, der Lateralwiderstand Wl ist viel größer als der Formwiderstand Wf). Die dabei entstehende Querkraft Q auf das Segel führt bei Einrumpfbooten zu einer Krängung, die ausgeglichen werden muss, damit das Boot nicht umkippt (siehe Abschnitt Stabilität).[2] Zu beachten ist, dass die Windkraft G im Segeldruckpunkt S angreift, während die Gegenkraft des Lateralplans Wl im Lateraldruckpunkt L angreift. Durch richtige Segeleinstellung und angepasste Krängung können die beiden Kräfte so ausgeglichen werden, dass das Boot weder luv- noch leegierig ist und nur die gleichförmige Fahrt vorwärts bei konstanter Krängung verbleibt.
Die beiden wirkenden Kräfte kann man näherungsweise auch numerisch bestimmen:[2][3]
mit K = Umrechnungskonstante (0,5 für Vortrieb, 1,32 für Querkraft, abhängig auch vom Kurs zum Wind), A = Segelfläche in m2, v = Geschwindigkeit des scheinbaren Winds in m/s, ρL = Dichte der Luft (~ 1,204 kg/m3). Das Ergebnis W ist die wirkende Kraft in Newton. Beispiel: Ein Boot mit einer Segelfläche von 35 m2 erzeugt bei einem scheinbaren Wind von 5 m/s einen Vortrieb von 263 N. Segelt das Boot mit 6 Knoten (3,09 m/s) entspricht dies einer Windleistung von 0,81 kW oder 1,09 PS.
Die Yacht beschleunigt so lange, bis sich Antriebs- und Widerstandskräfte die Waage halten. Der Formwiderstand ist der Widerstand, der dadurch entsteht, dass der Bootsrumpf bei der Fahrt durchs Wasser dieses zur Seite schieben muss. An der weglaufenden Bug- und Heckwelle erkennt man, dass dabei Energie verbraucht wird. Der Reibungswiderstand entsteht durch die Reibung des Wassers am Bootskörper. Er kann durch geeignete Oberflächenanstriche reduziert werden, was zugleich auch schädlichen Bewuchs am Bootskörper reduziert.[4] Schiffskonstrukteure versuchen, den Form- und den Reibungswiderstand so gering wie möglich zu halten, indem die Boote stromlinienförmig konzipiert werden und die durch das Wasser benetzte Fläche klein gehalten wird. Der Luftwiderstand entsteht an allen Teilen des Bootes, die über der Wasserlinie stehen: Überwasserschiff, Aufbauten, das Rigg und auch die Crew. Auf Kursen vor dem Wind hilft jeglicher Luftwiderstand allerdings dem Vortrieb.
Entscheidend beeinflusst wird der Vortrieb am Segel – und damit die Antriebskraft und die Geschwindigkeit des Bootes – durch den Winkel zwischen Segel und Wind, dem sogenannten Anstellwinkel. Ist dieser Winkel zu klein, beginnt das Segel zu killen (flattern). Ist der Winkel zu groß, reißt die Luftströmung auf der Leeseite des Segels ab, es entstehen Luftwirbel und der Auftrieb bricht zusammen. Durch Trimmen wird der richtige Winkel zwischen Segel und Wind eingestellt.
Der Windeinfallswinkel wird nicht nur durch den Kurswinkel des Schiffes zum tatsächlichen Wind, sondern auch von seiner eigenen Geschwindigkeit geprägt. Der für die Segel relevante wirksame Wind, der scheinbare Wind, wird immer vorlicher einfallen als der wahre Wind. Da auch die Geschwindigkeit des scheinbaren Windes mit der Bootsgeschwindigkeit zunimmt, ist es möglich, schneller als der Wind zu segeln. Wegen des immer vorlicher einfallenden Windes bei zunehmender Geschwindigkeit wird man dadurch auch die Segel immer dichter fahren müssen. Aus Sicht der Crew fährt ein schnelles Segelschiff daher sehr häufig Amwindkurs, auch wenn der wahre Wind achterlich einfällt.
Hydrodynamik

.JPG.webp)
Bedeutend für die Segeleigenschaften eines Schiffes ist neben dem Rigg, wie oben bereits angedeutet, auch das Unterwasserschiff. Der Konstrukteur legt über den Längsriss den sogenannten Lateralplan fest. Dies ist die seitliche Widerstandsfläche des Unterwasserschiffes, mit der die Abdrift verhindert wird.[5] Zum Lateralplan gehören auch Kiel, Ruder und eventuelle Leitflossen.[5] Der Lateraldruckpunkt ist der Punkt, an dem man sich die Querkräfte vereinigt denken kann. Er ist allerdings nicht statisch, sondern ändert sich mit der Krängung des Schiffes. Je stärker das Schiff krängt, umso weiter wandert der Lateraldruckpunkt nach vorne, weil hauptsächlich der Bug immer tiefer ins Wasser dringt, der tiefe Kiel und das Ruder aber immer höher steigen.
Die dynamischen Kräfte am Unterwasserschiff sind im nebenstehenden Diagramm 5 dargestellt. Tatsächlich ist nämlich nicht die aufrichtende Wirkung des Kiels für die Kraft Wl in Richtung Luv verantwortlich, diese kontert nur das Drehmoment um die Längsachse. Die Seitenkraft nach Luv wird dadurch aufgebaut, dass auch die Kielflosse wie eine Tragfläche wirkt. Der Anstellwinkel ist dabei der Driftwinkel (Winkel zwischen anliegendem Kurs K und Kurs durchs Wasser K’, in der Literatur mit oder angegeben).[6] Die Theorie schlanker Körper liefert dazu noch einen interessanten Zusammenhang. Der hydrodynamische Auftrieb des Kiels bestimmt sich als


mit L = Auftrieb, C = Umrechnungskonstante, = Dichte des Wassers, = Geschwindigkeit durchs Wasser, T = Tiefgang, = Tiefgang des Bootskörpers.[7] Aus der Formel folgt, dass mit erster Näherung der Auftrieb nicht von der Fläche des Kiels, sondern nur vom Quadrat des Tiefgangs abhängig ist. Dies bedeutet, dass der Kiel verkürzt werden kann, ohne den Auftrieb zu verringern, was genau der Entwicklung der Kielformen über die Zeit entspricht. Die Verkürzung hat den Vorteil, dass dadurch der Reibungswiderstand des Rumpfes verringert wird. Nachteilig ist allerdings die geringere Kursstabilität und das nervösere Verhalten am Ruder, sowie für den Konstrukteur die Herausforderung, die großen Querkräfte an der kleinen Auflagefläche des Kiels sicher in den Rumpf einzuleiten.
Rechnerisch muss zum Auftrieb am Kiel auch noch der Auftrieb am Ruder berücksichtigt werden, denn dieses wirkt ebenso als symmetrische aerodynamische Tragfläche, lediglich mit geringerer Fläche. Üblicherweise ist das Ruder außerdem weniger tief als der Kiel, das hat aber vorwiegend praktische Gründe: Beim unglücklichen Fall einer Grundberührung hält der massive Kiel deutlich mehr aus als das vergleichsweise filigrane Ruderblatt.
Wie bereits weiter oben ausgeführt, hat die Form des Unterwasserschiffes einen wesentlichen Einfluss auf die Segeleigenschaften. Der Rumpf soll möglichst stromlinienförmig sein, damit das Schiff geschmeidig durch die See fährt. Bei Kielbooten soll das Kielgewicht möglichst schwer sein und möglichst tief angebracht werden, um dessen Hebelwirkung zu maximieren und die hydrodynamischen Auftriebskräfte zu maximieren. Es ist Aufgabe des Bootskonstrukteurs, diese teilweise widersprüchlichen Anforderungen gegeneinander abzuwägen und entsprechend dem Verwendungszweck des Bootes anzupassen. Schnelle Regattaboote haben heute einen sehr flachen Rumpf mit einem tiefen Kiel, sie können damit teilweise Gleitfahrt erreichen. Fahrtensegler bevorzugen etwas rundere und tiefere Rümpfe mit geringerem Tiefgang, da diese zusätzlichen Wohnraum bieten, sanfter durch die Wellen gleiten und auch kleinere Häfen und Buchten angelaufen werden können. Auch das bei Fahrtenyachten generell größere Gesamtgewicht – im Verhältnis zur Bootslänge – erhöht den Komfort, da ein schwereres Boot weniger in den Wellen tanzt. Zum Nachteil wird das große Gewicht bei wenig Wind, weil solche schweren Boote dann erst ab einer bestimmten Windstärke überhaupt sinnvoll gesegelt werden können.
Interaktionen des Wassers mit dem Bootskörper
Windwellen
Das Segelschiff bewegt sich an der Grenzschicht von Luft und Wasser. Das im physikalischen Sinne als „Oberflächenwellen“, im üblichen Sprachgebrauch einfach als „Wellen“, bezeichnete Phänomen hat einen wesentlichen Einfluss auf die Fortbewegung mit einem Schiff. Für den Segler sind sie oft nur lästig, da sie einen bremsen können, wenn sie von vorne gegen den Bug schlagen und nicht selten dabei auch noch das Deck fluten. Zudem verursachen sie dynamische Bewegungen (Gieren um die Hochachse, Rollen um die Längsachse, Stampfen um die Querachse), die unangenehm sind und Seekrankheit verursachen können. Die Energie einer Welle kann ein Schiff zum Kentern bringen, besonders wenn sie direkt von der Seite aufschlägt, denn die kinetische Energie des sich bewegenden Wassers kann allein aufgrund seiner Masse enorm werden.
Vom Schiff erzeugtes Wellensystem
Während die Wirkung der Windwellen auf das Schiff für jeden Beobachter offensichtlich sind, gilt das nicht für die Wellen, die das Schiff selber erzeugt. Zunächst einmal erzeugt ein Schiff – bei hinreichender Wassertiefe und flachem Wasser – ein immer gleich aussehendes Wellensystem (siehe Video). Die Form dieses Systems ist erstaunlicherweise unabhängig von der Geschwindigkeit des Schiffes und der Dichte der Flüssigkeit. Das Wellensystem öffnet sich mit einem Winkel, der durch
gegeben ist. Es handelt sich um eine rein geometrische Eigenschaft von Wellen, die aus der Tatsache herrührt, dass das Wellenbild relativ zum bewegten Schiff stationär ist. Zusätzlich spielt die sogenannte Dispersionsrelation für Tiefwasserwellen eine Rolle:
wird dabei auch als Phasengeschwindigkeit der Wellen bezeichnet.[8] Dies kann man als Zahlenwertgleichung
schreiben oder mit bei der Seefahrt üblicheren Einheiten
was die Phasengeschwindigkeit der Wellen in Relation zur Wellenlänge setzt.
Die vorstehende Formel wird oft auch geschrieben als
mit der Wasserlinienlänge L eines Schiffes statt der Wellenlänge . Dies ist nämlich genau die als Rumpfgeschwindigkeit bekannte Größe. Im Zusammenhang mit der Rumpfgeschwindigkeit wird auch oft die sogenannte Froude-Zahl genannt. Dies ist eine dimensionslose Kennzahl, die die Wellenlänge des vom Schiff erzeugten Wellensystems in Relation zur Länge des Schiffes stellt:
mit vs = Schiffsgeschwindigkeit, g = Schwerebeschleunigung, L = Wasserlinienlänge. Die Schiffsgeschwindigkeit ist gleich der Phasengeschwindigkeit des Wassers. Durch Einsetzen des rechten Terms aus Gleichung (*) wird daraus:
Mit der Froude-Zahl lassen sich nun die Wellensysteme verschiedener Schiffe miteinander vergleichen. Ein Schiff, das mit einer Froude-Zahl kleiner als 0,4 unterwegs ist, fährt unterhalb seiner Rumpfgeschwindigkeit, denn die Wellenlänge des erzeugten Wellensystems ist kürzer als die Wasserlinienlänge. Bei Erreichen der Froude-Zahl 0,4 nimmt der Wasserwiderstand exponentiell zu, denn jetzt erzeugt das Schiff ein Wellensystem, das genau eine Wellenlänge lang ist. Am Bug befindet sich dabei der Wellenberg, am Heck das Tal. Um weiter beschleunigen zu können, muss das Schiff die eigene Bugwelle „überfahren“. Dies ist genau der Punkt, an dem ein Gleiter – ausreichende Antriebsleistung in Form von Windenergie vorausgesetzt – in Gleitfahrt übergehen kann. Dies ist jedoch nur bei leichten Booten mit flachem Rumpf der Fall.
Luv- und Leegierigkeit

Da ein Boot immer so konstruiert wird, dass der Segeldruckpunkt S im Lee des Lateraldruckpunktes liegt, entsteht durch das Kräftepaar Vortrieb V und Formwiderstand Wf ein Drehmoment nach Luv. Dieses nimmt umso stärker zu, je mehr das Boot krängt, denn dadurch wird der Hebelarm größer. Dagegen wirkt das Kräftepaar aus Querkraft Q und Widerstand des Lateralplans Wl, das ein Drehmoment nach Lee erzeugt. Das Drehmoment nimmt zu, wenn der Segeldruckpunkt zu weit nach vorne wandert, etwa weil die Segelflächen der verschiedenen Segel nicht im richtigen Verhältnis zueinander stehen.
Bei einem korrekt konstruierten Schiff und korrekt eingestellter Trimmung der Segel halten sich die beiden Kräfte die Waage und das Schiff fährt selbst bei festgesetztem Ruder geradeaus. Segelschiffe sind bewusst so konstruiert, dass sie bei zunehmender Krängung – etwa durch zunehmenden Wind – immer luvgieriger werden. Durch das Anluven reduziert sich die Krängung automatisch wieder, und falls keine Gegenmaßnahmen ergriffen werden, wird ein Sonnenschuss folgen: Der Bug dreht sich in den Wind und das Schiff bleibt stehen. Würde das Boot in so einem Fall nach Lee ausbrechen, würde die Krängung deutlich zunehmen (weil der Wind dann quer auf das Segel drückt) und eine Kenterung provozieren. Ein Schiff, das auf einem Raumschotskurs leegierig ist, begünstigt zudem eine gefährliche Patenthalse.
Stabilität

Eine wesentliche Aufgabe des Kiels oder Schwertes besteht darin, dem seitlich wirkenden Winddruck auf das Segel einen Widerstand unter Wasser entgegenzusetzen, um die Abdrift nach Lee zu verringern. Die daraus resultierende Schräglage des Bootes wird als Krängung bezeichnet. Auch durch Seegang kann ein Boot in Krängung versetzt werden. Unter der Stabilität eines Bootes wird seine Fähigkeit, diese Krängung auszugleichen und selbständig wieder in die aufrechte Lage zurückzukehren, verstanden. Dies kann auf zwei unterschiedliche Arten geschehen: einerseits durch Formstabilität, bei der die Rumpfform des Bootes eine Rückkehr in die Ausgangslage begünstigt, und andererseits durch Gewichtsstabilität, bei der ein tief liegender Ballastkiel das Boot wieder in die aufrechte Lage zwingt.
Bei gewichtsstabilen Yachten erzeugt der Ballastkiel ein aufrichtendes Drehmoment, das mit zunehmender Krängung immer stärker wird. Ein solches Boot besitzt eine geringe Anfangsstabilität, aber eine hohe Endstabilität, und kann nur unter sehr schweren Wind- und Seegangsbedingungen kentern. Da durch die Krängung gleichzeitig der Winddruck im Segel abnimmt, ist auch große Schräglage allein für das Boot nicht kritisch – allerdings potentiell für die Crew ungemütlich. Die Rumpfform bevorzugt außerdem einen bestimmten Krängungswinkel, sodass durch rechtzeitiges Reffen die Geschwindigkeit wieder zunehmen kann. Bei formstabilen Booten, wie beispielsweise einer Jolle, erfolgt der Ausgleich der Krängung durch den Auftrieb des Bootskörpers und eine Verlagerung des Mannschaftsgewichtes nach Luv (Ausreiten).
Dynamisches Verhalten
Die bisherigen Betrachtungen gingen von der Annahme aus, das Boot befinde sich in einem statischen Fahrzustand oder zumindest, dass es diesen nach kurzem Ungleichgewicht wieder erreiche. Dies ist aber in mehreren Betrachtungsfällen nicht zutreffend, etwa weil das Boot den Kurs ändern sollte oder weil es im Seegang zum „Tanzen“ gebracht wird.
Änderung des Momentengleichgewichts: Ablegen
Der erste Zeitpunkt, bei dem sich das Momentengleichgewicht ändert und als Ergebnis schließlich der gleichförmige Fahrzustand der vorigen Abschnitte erreicht wird, ist das Ablegen.[9] Wir betrachten ein Boot, das mit gesetzten Segeln am Steg festgemacht ist. Die Geschwindigkeit durchs Wasser ist demzufolge Null, wodurch auch die hydrodynamische Auftriebskraft des Kiels Null ist. Der Wind wehe mit konstanter Geschwindigkeit in ablandiger Richtung (Ablegemanöver unter Segeln mit auflandigem Wind sind an sich schon anspruchsvoll genug). Auf das Schiff wirkt eine Kraft nach Lee, die jedoch in diesem Zustand nur zu Krängung führt.
Werden nun die Festmacherleinen losgeworfen, drückt der Wind das Boot zunächst vom Land weg. Dadurch nimmt es aber gleichzeitig auch Fahrt nach vorne auf, denn der Bug wird (bei langsamer Fahrt) schneller weggedrückt als das Heck. Dadurch entsteht jetzt die Strömung um den Kiel, die in der hydrodynamischen Seitenkraft resultiert, die der Kiel dem Segeldruck entgegensetzen muss, damit das Schiff bei Amwindkurs geradeaus fährt. Der Gleichgewichtszustand ist erreicht, wenn sich, wie in Diagramm 2 ersichtlich, die Unterwasserkraft des Kiels () und die Auftriebskraft des Segels () die Waage halten.
Änderung des Momentengleichgewichts: Wenden
Neben An- und Ablegen sind die wichtigsten Manöver auf einem Segelschiff Wende und Halse. Bei diesen Manövern ändern Luv und Lee ihre Plätze und die Segel stehen anschließend auf der anderen Bootsseite. Bezogen auf die physikalische Betrachtung heißt das, dass die Richtung des Auftriebsvektors des Segels und jene des hydrostatischen Auftriebsvektors vertauscht werden.
Nehmen wir an, das Boot segle gleichförmig auf Steuerbordbug.[10] Die Wende wird durch deutliches Ruderlegen des Rudergängers nach Luv (Backbord) eingeleitet. Dadurch entsteht ein Drehimpuls, denn die Auftriebskraft des Ruderblatts zeigt wegen des großen Anstellwinkels nun nach Lee (in geradliniger Fahrt zeigt die Auftriebskraft des Ruderblatts etwas nach Luv, um die Luvgierigkeit des Boots zu kompensieren). Das Boot reagiert prompt und luvt an, bis die Segel einfallen (killen), und wenn genügend Schwung vorhanden ist, dreht es weiter, bis der Wind von der anderen Seite in die Segel greift. Der Rudergänger muss jetzt „Stützruder“ geben, d. h., entgegen der Drehbewegung steuern, um mit einem Ruderauftrieb in die neue Leerichtung die Drehbewegung des Bootes aufzufangen. Wurde die Wende zügig durchgeführt, befindet sich noch genügend Fahrt im Boot, sodass auf dem neuen Kurs sofort die hydrodynamische Auftriebskraft des Kiels entsteht, natürlich jetzt in die neue Luvrichtung. Der Wind füllt das Segel und entwickelt dessen Auftriebskraft.
Es haben nun die Auftriebskräfte von Kiel und Segel ihre Richtung um 180° geändert, die Gesamtkräfte jedoch nicht, denn der neue Kurs (die Richtung des Vortriebsvektors) hat sich nur um den Wendewinkel von typischerweise etwa 90° geändert.
Schwingungsbewegungen
Ein Schiff in Fahrt erfährt durch Wellen Beschleunigungen in Längs-, Quer- und Hochrichtung, sowie um alle drei Achsen. Interessant ist dabei zunächst einmal die Beschleunigung in Hochrichtung, die zu einer vertikalen Tauchschwingung führt, wenn das Boot von Wellen angehoben und abgesenkt wird. Das Boot selbst reagiert darauf ähnlich einer Feder, denn je tiefer es eintaucht, umso größer wird der Auftrieb, der das Boot wieder in die Normallage bringen will. Die Eigenfrequenz des idealen Bootes hängt von der Masse m und einer vom Bootskörper abhängigen Federkonstante k ab. Für ein reales Boot liefert[11]
schon recht gute Schätzwerte ( = Fläche Schwimmwasserlinie, = Dichte des Wassers). Nun wird die Wellenfrequenz in der Regel nicht dieser Eigenfrequenz entsprechen, was physikalisch gesehen auf das Problem eines fremderregten Schwingungssystems hinausläuft. Im Bootsbau ist es erwünscht, möglichst zu vermeiden, dass das Boot mit seiner Eigenschwingung angeregt werden kann, denn eine Anregung eines Schwingkörpers mit seiner Eigenfrequenz führt zu einer sehr hohen Amplitude, die durchaus auch höher sein kann als jene des fremderregenden Systems (in diesem Fall den Wellen). Schiffe mit sehr kleiner Eigenfrequenz (etwa Katamarane mit geringer Wasserlinenfläche) werden als „wave-piercing“-Schiffe bezeichnet, da sie durch die Wellen durchfahren.
Äquivalente Betrachtungen können auch für Drehbewegungen angestellt werden. Auch hier gibt es Wellenmuster, die das Boot erheblich stärker rollen lassen können, als die Höhe der Wellen vermuten lassen würde. Die Kreisfrequenz der Rollschwingung wird formal dargestellt als
mit = metazentrische Höhe (näherungsweise der Abstand zwischen dem Wirkungspunkt des Auftriebs und dem Schwerpunkt) und = Trägheitsmoment. Aus Stabilitätsgründen wäre grundsätzlich ein großes wünschenswert, denn bei einer solchen Yacht ist eine Kenterung weniger wahrscheinlich. Sie nimmt die senkrechte Schwimmlage nämlich sehr schnell wieder ein. Dynamisch betrachtet kann das allerdings auch ein erheblicher Nachteil sein, denn eine schnelle (Rück-)Bewegung des Schiffes verursacht große Kräfte in der Takelage, was die Dimensionierung derselben nicht hergeben könnte. Es gibt in der Literatur etliche Beispiele von Entmastung durch zu steife (zu „stabile“) Konstruktionen.[12]
Literatur
- Wolfgang Püschl: Physik des Segelns. 1. Auflage, Wiley-VCH, Weinheim 2012, ISBN 978-3-527-41106-1.
- Joachim Schult: Segler-Lexikon. 13. Auflage, 2008, ISBN 978-3-7688-1041-8.
- Thomas Bock (Mitarb.), Petra Krumme (Red.): Seemannschaft. Handbuch für den Yachtsport. 30. Auflage, Delius Klasing, Bielefeld 2013, ISBN 978-3-7688-3248-9. (Seit 1929 mit wechselnden Mitarbeitern herausgegeben vom Deutschen Hochseesportverband „Hansa“, anfangs mit dem Untertitel Handbuch für Segler (und Motorbootfahrer), seit der 13. Auflage 1969 als Handbuch für den Yachtsport.)
- Ross Garret: The Symmetry of Sailing. Sheridan House, Dobbs Ferry 1996.
Weblinks
Einzelnachweise
- Die Literatur ist sich uneins darüber, ob sich ein Halbwindkurs auf den wahren oder den scheinbaren Wind beziehen soll.
- Seemannschaft. 28. Auflage, S. 157 f.
- Joachim Schult: Segler-Lexikon. Stichwort Windkraft F = CT · 0,615 · v2 · A mit CT zwischen 1,0 für Vorwindkurse und 1,5 für Amwindkurse.
- Spezielle Hinweise für den Regattasegler und die für Regattaboote verwendeten Antifoulings. Abgerufen am 26. Dezember 2012.
- Joachim Schult: Segler-Lexikon. Stichwort „Lateralplan“.
- Wolfgang Püschl: Physik des Segelns. S. 16 ff.
- Wolfgang Püschl: Physik des Segelns. S. 108 f.
- Wolfgang Püschl: Physik des Segelns. S. 124.
- Nach Ross Garret: The Symmetry of Sailing. In Wolfgang Püschl: Physik des Segelns. S. 169 f.
- Nach Ross Garret: The Symmetry of Sailing. Adaptiert von Wolfgang Püschl: Physik des Segelns. S. 171.
- Wolfgang Püschl: Physik des Segelns. S. 173.
- Wolfgang Püschl: Physik des Segelns. S. 177.