Flexagon
Flexagone sind gelenkig verbundene Polygone mit der Eigenschaft nach einer Faltmanipulation namens Pinch-Flexen neben ihrer Vorder- und Rückseite weitere Seiten zu offenbaren.[1]

Geschichte
Das erste Modell eines Flexagons wurde 1939 von dem britischen Studenten Arthur H. Stone an der Princeton University entdeckt: Er war zu der Zeit ein britischer Austauschstudent in den USA. Da das amerikanische Papierformat größer als das in Europa genutzte DIN A4-Format ist, musste Stone, um das neue Papier für seinen Ordner passend zu machen, einen Streifen des Papiers entfernen. Aus Langeweile in den Vorlesungen spielte er mit diesen Streifen, faltete sie in verschiedenste Formen. Eines seiner Ergebnisse war das wahrscheinlich[2] erste Trihexaflexagon. Die genannte Falteigenschaft dieses Papiermodells veranlasste ihn und seine Kommilitonen John W. Tuckey, Bryant Tuckerman und Richard Feynman zur Gründung eines Flexagon-Komitees und zur Prägung des Namens 'Flexagon' für diese Art Objekte[3]. 1956 wurden sie durch Martin Gardners Artikel im The Scientific American einem größeren Publikum vorgestellt. Weiterhin entdeckten und beschrieben sie wichtige Analyse-Prozeduren wie den Tuckerman-Traverse und das damit verbundene Feynman-Diagramm. Eine komplette mathematische Theorie der Flexagone (english: Flexigation) wurde 1940 von Tuckey and Feynman herausgearbeitet, die auch eine Anleitung zum Bau jeden beliebigen Flexagons enthält. Die Theorie wurde nie veröffentlicht, jedoch stückchenweise von anderen Mathematikern wiederentdeckt.
Jedoch gibt es keine stichhaltigen Nachweise, dass die Entdeckung der Flexagone sich so abgespielt hat, oder, dass es jemals tatsächlich diesen Bericht gab. Man könnte z. B. einwenden, dass das erste Flexagon, das Trihexaflexagon, ein sehr simples Möbiusband ist, das schon 1858 beschrieben worden ist, von dem es anscheinend aus Wien in der Vorkriegszeit Berichte gab. Dennoch stellte das Princeton-Committee den Startschuss für die Arbeit an Flexagonen dar: Zu dem Princeton Flexagon Committee wird auch Briants Vater Prof. Louis B. Tuckerman gezählt, der auch nach der Auflösung des Committees in Folge des Krieges (v. a. den Angriff auf Pearl Harbor) jedes Jahr den Gewinnern des Westinghouse Science Talent Search ein Flexagon vorstellte. Diese Art der Verbreitung führte zu dem ersten Bericht über Flexagone. Im Jahre 1956 wurden Flexagone durch Martin Gardners ersten Beitrag seiner Kolumne „Mathematical Games“ im Scientific American dem breiten Publikum bekannt gemacht. Fast zeitgleich folgte der erste Bericht von Oakley and Wisner, der über das deskriptive Level hinausging und Flexagone mathematisch analysierte. Es folgten eine kleine Vielzahl weiterer deskriptiver Artikel bis 1962, als Conrad und Hartlines am Research Institute for Advanced Studies in Baltimore erstellter Bericht über Flexagone veröffentlicht wurde. Dieser korrigiert nicht nur die Fehler, die in Oakley und Wisners Bericht gemacht wurden, sondern stellt eine Anleitung zur Konstruktion eines beliebigen Flexagons dar.
Manipulationsarten
Flexagone, bzw. Hexaflexagone werden üblicherweise mit dem Pinch-Flex manipuliert. Bei Flexagonen höherer Ordnung ist jedoch eine weitere Manipulationsart, der V-Flex möglich.[4] Squareflexagone, also Flexagone mit einer quadratischen Grundform werden durch noch unbenannte Manipulationsarten gefaltet, die der Bewegung des Buchaufschlagen gleichen.
Anleitung zum Bau eines Trihexaflexagons
1. Ein Trihexaflexagon wird aus 9 gleichseitigen Dreiecken gebildet, die wie in Abbildung 1 gezeigt, auf einem Streifen abgezeichnet sind.
2. Die Dreiecke werden auf Vorder- und Rückseite wie in Abbildung 1 markiert.
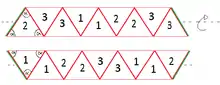
Der abgebildete Streifen wird als das Netz des Flexagons bezeichnet. Zur Beschriftung wurde der Streifen entlang der horizontalen Achse gewendet. So ist das erste Dreieck links auf seiner Vorderseite mit der Ziffer 2 und auf seiner Rückseite mit der Ziffer 1 markiert.
3. Die Linien zwischen den Dreiecken werden gefalzt.
4. Der Streifen ist so beschriftet, dass an drei Stellen zwei benachbarte Dreiecke die Ziffer 3 tragen (die Rückseite auch beachtend). Diese benachbarten Dreiecke werden gegeneinander gefaltet und somit zur Deckung gebracht. Abbildung 2 zeigt, wie die erste Faltung links vorgenommen wurde.
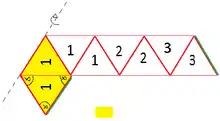
5. Keines der Dreiecke mit Beschriftung 3 ist nun sichtbar.
6. Die in den Abbildungen 1 und 2 grün gefärbten Endkanten werden aneinandergefügt, d. h. verklebt z. B. mit Tesafilm. Somit ergibt sich ein Sechseck.
7. Das Trihexaflexagon ist nun fertig (siehe Abbildung 3).
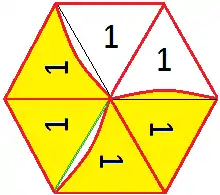
Nomenklatur
Beim Betrachten eines Trihexaflexagons, gebaut aus einem gesichterorientierten Netz, fällt auf, dass auf der Vorderseite alle sechs Dreiecksseiten mit der Ziffer 1 beschriftet sind. Auf der Rückseite sind alle sechs Dreiecksseiten mit der Ziffer 2 beschriftet. Das Flexagon wurde aus neun Dreiecken gebildet, besteht also aus achtzehn Dreiecksseiten (Vorder- und Rückseite). Das Flexagon zeigt nur 2 * 6 = 12 Dreiecksseiten; 6 Dreiecksseiten sind verdeckt, nämlich alle Dreiecksseiten, die mit der Ziffer 3 beschriftet sind.
Zur Nomenklatur: Die neun Dreiecke werden Dreiecksblätter oder allgemein Blätter genannt und die achtzehn Seiten Dreiecksseiten oder allgemein Seiten genannt.
Die Vorderseite mit sechs Seiten, die alle mit der Zahl "1" gekennzeichnet sind, und die Rückseite, bei der alle Seiten mit der Zahl "2" gekennzeichnet sind, sind Gesichter des Flexagons. Das Gesicht der Vorderseite wird in dieser Arbeit als Frontgesicht bezeichnet. Das Netz in Abbildung 1 wurde so beschriftet, dass die Seiten eines Gesichts alle gleich beschriftet sind. Diese Art Netz wird gesichterorientiertes Netz genannt.
Wie Abbildung 3 andeutet, ist das Frontgesicht kein regelmäßiges durchgehendes Hexagon, sondern es ist immer nach 2 Blättern, also insgesamt 3-mal, durch einen Spalt strukturiert. Wenn man zwischen die Spalten schaut, kann man die verborgenen 2 · 3 = 6 Seiten sehen.
Wenn man das flache Flexagon aus seiner zweidimensionalen Welt befreit, indem man die Spalten ein wenig öffnet, stellt man fest, dass durch das Zusammenbringen des Streifens ein Möbiusband gefertigt wurde.[5] Ein einfach verdrehtes Möbiusband wird aus einem Streifen gefertigt, indem man den Streifen an einem Ende um 180° dreht und die Enden verbindet. Beim Bau des Trihexaflexagons wurde der Streifen durch das Falten dreimal um 180° gedreht.[6] Das Gesicht des Flexagons zeigt sechs Seiten. Wenn man nicht nur die Seiten erfassen möchte, sondern alle Blätter des Flexagons berücksichtigt, ist die Einführung des Begriffs Blattbündel oder englisch: Pat notwendig. Das Flexagon besteht aus sechs Blattbündeln, die zusammen alle Blätter und damit auch alle Seiten des Flexagons umfassen.[7]
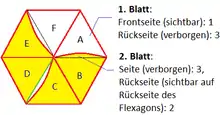
Das Blattbündel aus Standort A beinhaltet 2 Blätter mit 4 Seiten. Das obere Blatt hat eine sichtbare Seite, die Teil des Frontgesichts und mit 1 markiert ist, und eine Rückseite, die mit 3 markiert ist. Das untere Blatt hat eine sichtbare, mit 2 markierte Seite als Teil des rückwärtigen Gesichts und eine verborgene Seite, die mit 3 markiert ist. Das Blattbündel aus Standort B besteht aus nur einem Blatt, dessen zwei Seiten beide sichtbar als Teil der Gesichter sind. Die Anzahl des Blätter in einem Blattbündel ist gleich der Ordnung des Blattbündels. Folglich ist das Blattbündel an Standpunkt A eines der Ordnung 2, das Blattbündel an Standort B eines der Ordnung 1.
Die Blattbündel von Standort C und E entsprechen dem von Standort A. Die Blattbündel von Standort D und F entsprechen dem von Standort B. Somit wiederholt sich die A-B Sequenz dreimal in dem Flexagon. Daher kann man ein Flexagon allein mit zwei angrenzenden Blattbündeln ausreichend beschreiben. Zwei angrenzenden Blattbündel werden als Sektor bezeichnet (siehe Abbildung 6). Addiert man die Ordnung der zwei Blattbündel eines Sektors, so erhält man die Ordnung des Flexagons. Das Trihexaflexagon ist folglich ein Flexagon der Ordnung 3.
Benennung von Flexagonen
Flexagone werden nach ihrer Gesichtsanzahl und nach ihrer Form benannt. Die erste Vorsilbe gibt die Gesichtszahl an, die zweite die Anzahl der Ecken der Form. So hat ein Trihexaflexagon 3 = Tri verschiedene Gesichter und stellt ein Sechseck = Hexagon dar. Bei dem Zählen der Gesichter ist zu beachten, dass ausschließlich die Gesichter, die mit einem Pinch-Flex zustande gekommen sind, gezählt werden. Andere Manipulationsformen sind möglich, die auch andere Gesichter bilden, diese werden jedoch nicht berücksichtigt.
Ein Tetrahexaflexagon hat vier Gesichter und als geometrische Form ein Hexagon. Das Hexasquareflexagon hat 6 Gesichter und als geometrische Grundform ein Quadrat.
Variationen von Flexagonen
Hexaflexagon
Die Gruppe der Hexaflexagone umfasst alle sechseckigen Flexagone. Die üblichsten und bekanntesten Vertreter sind aus gleichseitigen Dreiecken gebaut, wie das erste Trihexaflexagon von Arthur H. Stone.
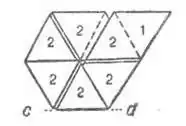
Trihexaflexagon: Dieses Flexagon besteht aus 9 gleichseitigen Dreiecken. Es gibt eine Variation.
Tetrehexaflexagon: Dieses Flexagon besteht aus 12 gleichseitigen Dreiecken. Es gibt eine Variation.
Pentahexaflexagon: Dieses Flexagon besteht aus 15 gleichseitigen Dreiecken. Es gibt eine Variation.
Hexahexaflexagon: Dieses Flexagon besteht aus 18 gleichseitigen Dreiecken. Es gibt drei Variationen.
Heptahexaflexagon: Dieses Flexagon besteht aus 21 gleichseitigen Dreiecken. Es gibt vier Variationen.
Tetraflexagon (Faltquadrat)
Beispiele sind Tritetraflexagon und Tetratetraflexagon.
Weblinks
Belege
- Pook, L.: (2003). Flexagons Inside Out, Cambridge: Cambridge University Press
- McIntosh, H.V.: (2000). My Flexagon Experiences, Puebla, Mexico: Departamento de Aplicación de Microcomputadoras, Instituto de Ciencias, Universidad Autononoma de Puebla.
- Gardner, M.: (1959). The Scientific American Book of Mathematical Puzzles and Diversions, New York: Simon and Schuster
- McLean, B.: (1979). V-Flexing the Hexahexaflexagon, The American Mathematical Monthly, Vol. 86, No. 6
- Oakley, C.O.; Wisner, R.J.: (1957). Flexagons, Haverford College: The American Mathematical Monthly, Vol. 64, No. 3
- Universität Bielefeld - Flexagone - online erhältlich unter: Flexagone. zuletzt aufgerufen am 12. Februar 2016
- Oakley, C.O.; Wisner, R.J.: (1957). Flexagons, Haverford College: The American Mathematical Monthly, Vol. 64, No. 3, S. 143