Mooresches Gesetz
Das mooresche Gesetz (englisch Moore’s law; deutsch „Gesetz“ im Sinne von „Gesetzmäßigkeit“) besagt, dass sich die Komplexität integrierter Schaltkreise mit minimalen Komponentenkosten regelmäßig verdoppelt; je nach Quelle werden 12, 18 oder 24 Monate als Zeitraum genannt.[1][2]
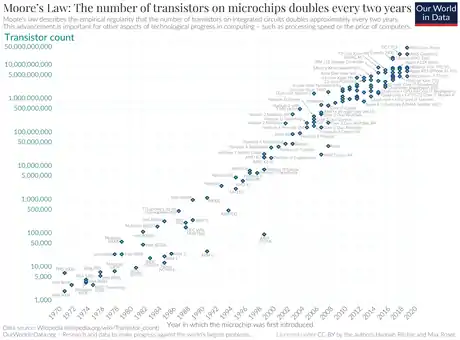
Unter Komplexität verstand Gordon Moore, der das Gesetz 1965 formulierte, die Anzahl der Schaltkreiskomponenten auf einem integrierten Schaltkreis. Gelegentlich ist auch von einer Verdoppelung der Integrationsdichte die Rede, also der Anzahl an Transistoren pro Flächeneinheit. Diese technische Entwicklung bildet eine wesentliche Grundlage der „digitalen Revolution“.
Geschichte
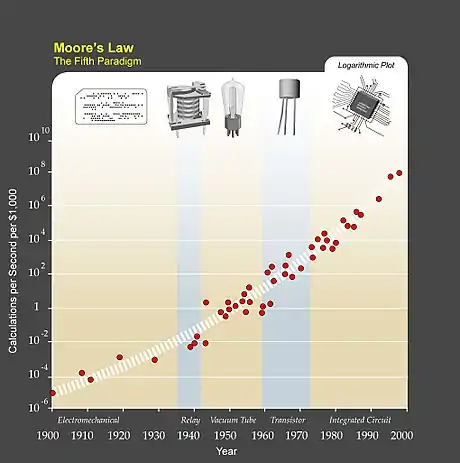
Gordon Moore äußerte seine Beobachtung in einem am 19. April 1965 erschienenen Artikel der Zeitschrift Electronics,[3] nur wenige Jahre nach Erfindung der integrierten Schaltung. Die Bezeichnung „mooresches Gesetz“ wurde um 1970 von Carver Mead geprägt. Ursprünglich sagte Moore eine jährliche Verdoppelung voraus, korrigierte diese Aussage jedoch 1975 in einer Rede vor der Society of Photo-Optical Instrumentation Engineers (SPIE) auf eine Verdoppelung alle zwei Jahre (siehe auch wirthsches Gesetz). Auslöser dafür war, dass sich die stürmische Entwicklung der Halbleitertechnik der ersten Jahre verlangsamt hatte. Neben der Verkleinerung von Elementen und der Vergrößerung der Wafer spielte in den ersten Jahren noch die von Moore so genannte „cleverness“ eine Rolle, nämlich die Kunst, Bauelemente intelligent auf dem Chip zu integrieren. Die Grenzen dieser Cleverness waren in den 1970er Jahren weitgehend ausgereizt. Moores damaliger Intel-Kollege David House brachte eine Abschätzung von 18 Monaten ins Spiel,[4] was heute die verbreitetste Variante des mooreschen Gesetzes ist und auch den Rahmen bildet, an dem die Halbleiterindustrie ihre Entwicklungspläne auf mehrere Jahre hinaus festmacht. Real verdoppelt sich die Leistung neuer Computerchips im Mittel etwa alle 20 Monate. In den Medien ist bis heute meist von einer Verdoppelung der Integrationsdichte alle 18 Monate die Rede.
Dieser Wert bezieht sich jedoch auf Angaben aus der Massenproduktion einer zu dem Zeitpunkt aktuellen Technologie-Generation. 2005 lief beispielsweise die konkurrenzfähige Herstellung der Chips für den Weltmarkt mit Strukturen zwischen 130 und 90 nm. In Vorbereitung für die Massenfertigung befand sich die 65-nm-Technik (Gatelänge je nach Technologie ca. 30 bis 50 nm) und im Labor befasste man sich damals bereits mit wiederum kleineren Strukturgrößen. So wurden schon erste Prototyp-Transistoren mit 10 nm Gatelänge gefertigt.[5]
Auf Intels Entwicklerforum (IDF) im Herbst 2007 sagte Moore das Ende seines Gesetzes voraus: Es werde wahrscheinlich noch 10 bis 15 Jahre Bestand haben, bis eine fundamentale Grenze erreicht sei. Allerdings prognostizierte Pat Gelsinger, Chef der Digital-Enterprise-Sparte von Intel, bereits ein halbes Jahr später, dass das mooresche Gesetz noch bis 2029 Gültigkeit behalten würde. Im Oktober 2009 erklärte Martin Strobel in seiner Funktion als Pressesprecher von Intel Deutschland im Detail, weshalb man zuversichtlich sei, „das mooresche Gesetz noch eine ganze Weile erfüllen zu können“.[6]
Abseits dieser technischen Fragen fällt bei der genauen Lektüre des Originalartikels aus dem Jahr 1965 allerdings auf, dass Moore keine wirkliche Begründung dafür liefert, warum die Entwicklung in dieser Geschwindigkeit und in dieser Form verlaufen sollte. Auch war zum damaligen Zeitpunkt die Entwicklung der Halbleitertechnik noch so neu, dass eine (z. B. lineare) Extrapolation des bisherigen Verlaufes in die Zukunft kaum hätte seriös genannt werden können. Stattdessen skizziert Moore ausführlich – und mit offensichtlicher Begeisterung – ein sehr weites Szenario möglicher zukünftiger Anwendungen in Wirtschaft, Verwaltung (und Militär), die zum damaligen Zeitpunkt aber – wenn überhaupt – allenfalls als Plan oder als grobe Vorstellung tatsächlich existierten. Dabei behauptet er zwar gleich am Anfang seines Artikels, dass „bis 1975 wirtschaftlicher Druck dazu führen würde, bis zu 65.000 Komponenten auf einen einzelnen Chip zusammenzuquetschen“ (… by 1975 economics may dictate squeezing as many as 65,000 components on a single silicon chip …), macht aber keine weiteren Angaben dazu, woher, in welcher Form oder auch von wem ein solcher wirtschaftlicher Druck ausgeübt werden sollte. Rückblickend und nachdem die Informationstechnik sich tatsächlich so rasant über mehrere Jahrzehnte hinweg entwickelt hat, ist es kaum noch möglich, die visionäre Kraft adäquat einzuschätzen, die damals von Gordon Moore für diese Prognose aufgebracht werden musste.
Auslegung
Moores Gesetz ist kein wissenschaftliches Naturgesetz, sondern eine Faustregel, die auf eine empirische Beobachtung zurückgeht. Gleichzeitig kann man von einer „selbsterfüllenden Prophezeiung“[7] sprechen, da verschiedenste Industriezweige an der Entwicklung besserer Mikrochips beteiligt sind. Sie müssen sich auf gemeinsame Meilensteine einigen (z. B. optische Industrie mit verbesserten lithographischen Methoden), um wirtschaftlich arbeiten zu können. Die Formulierung des mooreschen Gesetzes hat sich im Laufe der Zeit stark verändert. Sprach Moore noch von der Komponentenanzahl auf einer integrierten Schaltung, so ist heute von der Transistoranzahl auf einer integrierten Schaltung die Rede, mitunter sogar von der Transistoranzahl pro Flächeneinheit.
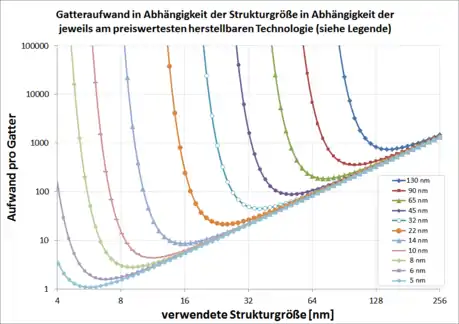
Moore stellte fest, dass die Kosten einer Schaltkreiskomponente verfahrensbedingt sowohl mit sinkender als auch mit steigender Komponentenanzahl anstiegen. Bei niedriger Komponentenanzahl wurde das verfügbare Material nicht voll ausgenutzt, für höhere Komponentenanzahlen mussten experimentelle Verfahren eingesetzt werden, die sich wirtschaftlich noch nicht lohnten. Er bezog seine Beobachtung daher ausschließlich auf das jeweilige Kostenoptimum, also dasjenige Produktionsverfahren und diejenige Komponentenanzahl pro Schaltkreis, bei denen die Kosten pro Schaltkreiskomponente am geringsten ausfielen. Dadurch ist theoretisch klar vorgegeben, welches Herstellungsverfahren und welcher Computerchip zur Überprüfung des mooreschen Gesetzes in jedem Jahr betrachtet werden müssten.
Die unterschiedlichen Formulierungen verzerren die ursprüngliche Beobachtung Moores teilweise bis zur Unkenntlichkeit. Bereits die variable Auslegung des Verdoppelungszeitraums von 12, 18 oder 24 Monaten verursacht beträchtliche Unterschiede. Da Computerchips stark in der Größe variieren, ist es auch nicht dasselbe, ob man die Transistoranzahl pro Chip oder pro Flächeneinheit betrachtet. Das Weglassen des Kostenoptimums schließlich führt zu einer vollständigen Entfremdung. Ohne Kostenoptimum kann jedes beliebige Produktionsverfahren und jeder beliebige Schaltkreis zur Bestätigung des mooreschen Gesetzes herangezogen werden; ob es sich um einen handelsüblichen Prozessor, extrem teure Hochtechnologie oder experimentelle Schaltkreise, die noch gar nicht auf dem Markt sind, handelt, ist in dieser laxen Auslegung ohne Belang. Durch die unterschiedlichen kursierenden Versionen hat das mooresche Gesetz viel von seiner objektiven Aussagekraft eingebüßt.
Schreibweise
Die Komplexität in Abhängigkeit mit der Zeit des mooreschen Gesetzes folgt einer Exponentialfunktion:
Dabei ist die Rate der Zunahme der Kehrwert der Verdopplungszeit , multipliziert mit der Konstanten :
Dieser Zusammenhang kann auch in der verkürzten Schreibweise:
dargestellt werden.
Für die Verdopplungszeit sind mehrere Annahmen gebräuchlich. Oftmals wird verwendet, beträgt in diesem Fall 0,35 pro Jahr.
Rechenleistung
Dass mit der Anzahl der Transistoren auf einem Computerchip auch die Rechenleistung der Computer linear anwächst, kann aus dem mooreschen Gesetz nicht gefolgert werden. Bei modernen Prozessoren werden immer mehr Transistoren für einen integrierten Speicher (Cache) verwendet, der zur Rechenleistung nur passiv beiträgt, indem er Zugriffe auf häufig benötigte Daten beschleunigt. Als Beispiel sei hier der Vergleich zweier Prozessoren aus der Reihe des Pentium III gegeben. Dabei handelt es sich zum einen um einen „Katmai“ mit einer Taktfrequenz von 500 MHz und externem L2-Cache, zum anderen einen „Coppermine“ in der 1-GHz-Variante mit integriertem L2-Cache. Dabei hat sich beim 1-GHz-Coppermine gegenüber dem 500-MHz-Katmai die Taktfrequenz verdoppelt und die Transistoranzahl sogar verdreifacht, dennoch zeigt sich bei diesen vergleichsweise ähnlichen Prozessoren eine Leistungssteigerung um den Faktor 2,2 bis 2,3.
| Prozessor | Transistoren | SPEC-Werte | |
|---|---|---|---|
| Ganzzahl | Gleitkomma | ||
| Pentium III 500 MHz (externer L2-Cache) | 9,5 Mio. | 20,6 | 14,7 |
| Pentium III 1000 MHz (interner L2-Cache) | 28,5 Mio. | 46,8 | 32,2 |
In Mehrkernprozessoren werden mehrere Prozessorkerne auf einem Chip zusammengeführt, die parallel arbeiten und dadurch mehr Leistung erbringen. Hier wird die Verdoppelung der Transistoranzahl hauptsächlich durch die Verdoppelung der Anzahl der Prozessorkerne erreicht. Auch hier tritt jedoch keine Verdoppelung der Rechenleistung ein, denn beim Parallelbetrieb der Prozessorkerne fällt zusätzlicher Koordinierungsaufwand an, der die Leistung wieder schmälert (siehe Skalierbarkeit). Zudem sind nicht alle Programmteile im Betriebssystem und bei Anwendungen parallelisierbar, so dass es schwierig ist, alle Kerne gleichzeitig voll auszulasten. Eine einführende Übersicht zu diesem Thema bietet das amdahlsche Gesetz.
Grenzen
Neben Kritik an der fehlerhaften Auslegung des Gesetzes selbst gab es stets Zweifel, dass der Trend noch lange anhalten würde, die sich bisher nicht bestätigten. Vielmehr begann das mooresche Gesetz in den 1990er-Jahren als selbsterfüllende Prophezeiung zu wirken, indem sich Pläne zur Koordination der Entwicklungstätigkeiten hunderter Zulieferer daran orientierten.[8] Technologische Hürden wurden so mit immer höherem Kapitaleinsatz just-in-time gemeistert, siehe Technologieknoten. Wächst der finanzielle Aufwand für Entwicklung und Herstellung integrierter Schaltungen schneller als die Integrationsdichte, könnten sich die Investitionen bald nicht mehr lohnen. Das ist wahrscheinlich bei Annäherung an physikalische Grenzen, die aufgrund des quantenmechanischen Tunnelstroms bei 2 bis 3 nm liegen.[8] Derzeit (2016) fertigt Intel 14-nm-Prozessoren. Der Hersteller nahm an, bis Ende 2015 die 10-nm-Technik auf den Markt bringen zu können. Allerdings wird sich deren Auslieferung vermutlich um zwei Jahre verzögern. Die 2016 veröffentlichte Roadmap folgt nicht mehr dem mooreschen Gesetz.[8]
Derzeit werden daher zahlreiche Lösungsansätze zur Ablösung der klassischen Halbleitertechnik erprobt.[9] Kandidaten für grundsätzlich neue Technologien sind die Erforschung von Nanomaterialien wie Graphen, dreidimensionale integrierte Schaltkreise (und somit die Erhöhung der Transistorzahl pro Volumen und nicht mehr nur pro Fläche), Spintronik und andere Formen mehrwertiger Logik,[10] sowie Tieftemperatur- und Supraleiter-Computer, optische und Quantencomputer. Bei all diesen Technologien würde die Rechenleistung oder Speicherdichte gesteigert, ohne im herkömmlichen Sinn die Dichte an Transistoren zu steigern, so dass das mooresche Gesetz zwar formell an Gültigkeit verlöre, nicht aber zwingend von seinen Auswirkungen her.
Auf der Anwendungsseite werden mit zunehmender Integrationsdichte Engpässe an anderer Stelle deutlich, die durch weitere Integration nicht lösbar sind. Im Bereich höchster Rechneranforderungen (speziell: numerische Strömungssimulation auf Rechnern mit zahlreichen Kernen) ist dagegen seit etwa 2003 eine deutliche Verletzung des mooreschen Gesetzes zu beobachten, siehe Speedup. Die Zeit, die je finitem Volumen (cell) und je Iteration des Solvers benötigt wird, sinkt seither gar nicht oder nur noch marginal. Grund ist der Von-Neumann-Flaschenhals.[11] Tatsächlich werden viele integrierte Schaltungen gar nicht an dieser Grenze betrieben, eine höhere Rechenleistung würde sich dann nicht unmittelbar als Anwendernutzen niederschlagen.
Weitere Rezeption
Sherry „Lass“ Lassiter, Vorstandsvorsitzende der Fab Foundation, stellte 2016 in Anlehnung an Moore das lasssche Gesetz (Lass' Law) auf, nach der sich die Anzahl an FabLabs und unter Open-Source-Hardware-Kriterien erstellter Produktionsmaschinen in ähnlicher Weise jährlich verdoppele.[12] Neil Gershenfeld sieht die Phänomen als nächsten Schritt der virtuellen und distributiven Produktentstehung.[13]
Literatur
- Scott Hamilton: Taking Moore’s law into the next century. In: Computer. Band 32, Nr. 1, 1999, S. 43–48, doi:10.1109/2.738303 (englisch).
- The Technical Impact of Moore’s Law. In: M. Y. Lanzerotti (Hrsg.): IEEE solid-state circuits society newsletter. Band 20, Nr. 3, 2006 (englisch, ieee.org [PDF; 1,3 MB]).
- R. R. Schaller: Moore’s law: past, present and future. In: IEEE Spectrum. Band 34, Nr. 6, 1997, S. 52–59, doi:10.1109/6.591665 (englisch).
- Christoph Drösser: Die Wie-schnell-wird-aus-Technik-Schrott-Formel. In: Die Zeit. Nr. 16/2005. 14. April 2005.
Weblinks
- The Silicon Engine | 1965 – „Moore’s Law“ Predicts the Future of Integrated Circuits. In: Computer History Museum. (englisch)
- Ray Kurzweil: The Law of Accelerating Returns. In: kurzweilai.net. 7. März 2001 (englisch, Artikel, in dem Kurzweil ausgehend vom mooreschen Gesetz die Beschleunigung der technologischen Entwicklung prognostiziert).
- Jürgen Kuri: Vor 40 Jahren: Electronics druckt Moores Gesetz. In Heise online, 19. April 2005 (Artikel über die Hintergründe und Umstände der Veröffentlichung)
- Ilkka Tuomi: The lives and deaths of moores law. In First Monday, Volume 7, Nummer 11. 4 November 2002 (peer reviewed, englisch)
- Bernd Kling: Nvidia-CEO: Moore’s Law ist am Ende. In ZDNET, 10. Januar 2019
Einzelnachweise
- R. Hagelauer, A. Bode, H. Hellwagner, W. Proebster, D. Schwarzstein, J. Volkert, B. Plattner, P. Schulthess: Informatik-Handbuch. 2. Auflage. Pomberger, München 1999, ISBN 3-446-19601-3, S. 298–299.
- Robert Schanze: Mooresches Gesetz: Defintion und Ende von Moore's Law – Einfach erklärt. In: GIGA. 25. Februar 2016, abgerufen am 15. Oktober 2019.
- G. E. Moore: Cramming more components onto integrated circuits. In: Electronics. Band 38, Nr. 8, 1965, S. 114–117 (intel.com [PDF]).
- Michael Kanellos: Moore’s Law to roll on for another decade. In: CNET News. 11. Februar 2003. (englisch)
- R. Chau, B. Doyle, M. Doczy, S. Datta, S. Hareland, B. Jin, J. Kavalieros, M. Metz: Silicon nano-transistors and breaking the 10 nm physical gate length barrier. In: Device Research Conference, 2003. 2003, S. 123–126, doi:10.1109/DRC.2003.1226901.
- Wir sind zuversichtlich, das Mooresche Gesetz noch eine ganze Weile erfüllen zu können. In: MacGadget. 19. Oktober 2009, abgerufen am 20. Juni 2011.
- Gordon Moore bezeichnet sein Gesetz als eine „self fulfilling prophecy“, siehe Gordon Moore says aloha to Moore’s Law. In: The Inquirer. 13. April 2005, abgerufen am 4. März 2009 (englisch).
- M. Mitchell Waldrop: The chips are down for Moore’s law. News Feature, Nature 530, Februar 2016, doi:10.1038/530144a.
- Stefan Betschon: Die Informatik braucht einen Neustart. In: Neue Zürcher Zeitung. Internationale Ausgabe. 2. März 2016, S. 37.
- Moore’s Law, Part 2: More Moore and More than Moore (Memento vom 13. November 2013 im Webarchiv archive.today)
- Rainald Löhner, Joseph D. Baum: On maximum achievable speeds for field solvers. In: International Journal of Numerical Methods for Heat & Fluid Flow. 2014, S. 1537–1544, doi:10.1108/HFF-01-2013-0016 (englisch).
- Roberto Saracco: Lass’ Law is knocking at the door. 9. März 2018, abgerufen am 1. Februar 2021 (amerikanisches Englisch).
- Alan Gershenfeld, Joel Cutcher-Gershenfeld: Designing reality : how to survive and thrive in the third digital revolution. First edition Auflage. New York, ISBN 978-0-465-09347-2.