Mittelmaße der Architektur
Die Mittelmaße in der Architektur bezeichnen ein Proportionssystem, bei dem verschiedene Größen, etwa Länge, Breite und Höhe eines Raumes, proportional in Abhängigkeit gebracht werden, indem sie harmonisch gebunden werden. Die erste Anwendung in der Architektur beschreibt Vitruv, als es darum geht die Höhe eines Raumes zu bestimmen.[1] Ausführlichere Beschreibungen geben Leon Battista Alberti und Andrea Palladio, letzterer liefert in seinen Vier Büchern zur Architektur auch Beispiele.
Demnach sollen das arithmetische, das geometrische oder das harmonische Mittel helfen, um etwa bei einem festgelegten Grundriss zur gewählten Länge und Breite die Höhe zu finden. Aus diesen Maßen lassen sich so die Proportion des nachfolgenden Raumes bestimmen. Auch ein gesamtes Bauwerk lässt sich vom Ganzen über die Mittelmaße proportional teilen. Ein Beispiel:
Ein Raum sei beispielsweise 12 m lang und 6 m breit. Beim arithmetischen Mittel (besser bekannt als Durchschnitt) wäre die Höhe 9 m, das harmonische Mittel ergibt die Höhe von 8 m, das geometrische Mittel liegt bei 8,46 m.
Philosophischer Ansatz zur Bedeutung der Mittelmaße
Alberti schreibt in seiner Baukunst: "Derart machen die Architekten mittels dieser mittleren Proportionalen die schönsten Entwürfe sowohl für das ganze Gebäude als für die Teile des Bauwerkes..."[2] Alberti definiert die Schönheit als "eine Art Übereinstimmung und ein Zusammenklang der Teile zu einem Ganzen, das nach einer bestimmten Zahl, einer besonderen Beziehung und Anordnung ausgeführt wurde, wie es das Ebenmaß, das heißt das vollkommenste und oberste Naturgesetz, erfordert."[3]
Die Philosophen des Mittelalters fußen in ihrer Ästhetik sehr stark auf antike Vorfahren. So führt Umberto Eco aus, dass Augustinus Cicero fast wörtlich zitiert wenn er fragt: "Woraus besteht körperliche Schönheit? Im richtigen Verhältnis der Teile zueinander ..."[4][5][6] Für Eco ist die Ästhetik der Proportion eine Ästhetik der Quantitäten.[7]
Platon und Aristoteles haben sich an verschiedenen Stellen ihrer Schriften zu Proportionen und Mittelmaße geäußert. So hält es Platon für unmöglich zwei Dinge ohne ein drittes, verbindendes schön zusammen zufügen. Nur ein vermittelndes Band kann zwischen ihnen eine Verbindung herstellen.[8] Die Vermittlung zweier unterschiedlicher Größen übernehmen die Mittelmaße um über ein drittes die beiden vorigen zu binden.
Die rechnerische Bestimmung der Mittelmaße
Die Mittelmaße lassen sich rechnerisch bestimmen. Überraschend ist der unterschiedliche Ansatz, die unterschiedliche Sichtweisen und Bedeutungen der Mittelmaße offenbaren.
Die Berechnung des arithmetischen Mittels
Das arithmetische Mittel (aM) aus zwei Zahlen (hier stets a und b) zu bestimmen erfolgt üblicherweise mit der Formel: aM = (a + b) / 2.
Boethius geht um 500 n. Chr. so vor:
- a = 40, b = 10
- Differenz bilden: d = a - b = 40 - 10 = 30
- Differenz halbieren: 30 / 2 = 15
- Die halbe Differenz zur kleineren Zahl hinzu addieren: 15 + 10 = 25 = aM[9]
Die Berechnung des geometrischen Mittels
Das geometrische Mittel (gM) lässt sich numerisch nur über die Multiplikation der beiden Ausgangszahlen und dem Ziehen der Quadratwurzel daraus bestimmen:
- a = 40, b = 10
- √(a * b) = √(40 * 10) = 400
- √400 = 20 = gM
Da bis zur Renaissance das Wurzelziehen kaum möglich war, so Alberti und Palladio, verweisen sie auf die grafische Bestimmung des geometrischen Mittels. Beide verwenden das gleiche Zahlenbeispiel (Proportion 9:4 mit dem gM 6).[10]
Die Berechnung des harmonischen Mittels
In der Literatur finden sich unterschiedliche Herangehensweisen zur rechnerischen Bestimmung des harmonischen Mittels (hM) aus zwei Zahlen:
Heute gilt die Formel: hM = 2 * a * b / (a + b)
- a = 40, b = 10
- hM = 2 * a * b / (a + b) = 2 * 40 * 10 / (40 + 10) = 800 / 50 = 16
Boethius rechnet so:
- a = 40, b = 10
- Addieren der beiden Zahlen: s = a + b = 40 + 10 = 50
- Differenz bilden : d = a - b = 40 - 10 = 30
- Die kleinere Zahl mit der Differenz multiplizieren: m = b * d = 10 * 30 = 300
- Das Produkt mit der Summe der beiden Zahlen teilen: t = m / s = 300 / 50 = 6
- Dieses Ergebnis zur kleineren Zahl addieren: hM = t + b = 6 + 10 = 16
Alberti rechnet so:
- a = 40, b = 10
- Das Verhältnis der beiden Zahlen zueinander finden, hier etwa 4 : 1
- Die beiden Verhältniszahlen addieren: 4 + 1 = 5
- Differenz bilden: d = a - b = 40 - 10 = 30
- Differenz durch die Summe der Verhältniszahlen teilen: 30 / 5 = 6
- Das Ergebnis zur kleinen Zahl hinzuaddieren: hM = 6 + 10 = 16[11]
Bei dieser Methode besteht die Schwierigkeit das geeignete Verhältnis zu den beiden Maßen zu finden.
Am einfachsten macht es Palladio (Sein Weg entspricht durch Umstellung der heutigen Formel):
- a = 40, b = 10
- Bestimmen des arithmetischen Mittels, aM = (a + b) / 2 = (40 + 10) / 2 = 25
- Multiplizieren der beiden Zahlen m = a * b = 40 * 10 = 400
- Teilen der Multiplikation durch das arithmetische Mittel: hM = (a * b) / aM = 400 / 25 = 16
Die Berechnung der Mittelmaße bei musikalischen Intervallen
Die Pythagoreer hatten die Tetraktys, das altgriechische Symbol für die Zahl 10, besonders herausgestellt, erlaubte dieses doch auf prägnante Weise ihr Weltbild zu veranschaulichen. An ihr lassen sich die Proportionen 1:2, 2:3 und 3:4 und auch die Proportionen 1:3 und 1:4 mit einem Monochord sowohl akustisch als auch (über die Saitenlängen) visuell erfahren. Diese Proportionen (Oktave, Quinte und Quarte; Duodezime und Doppeloktave) sind längst Bestandteil der Musiktheorie.
Der Raum mit den Maßen 12 m Länge und 6 m Breite bildet im Grundriss die Proportion der Oktave, das Verhältnis 2 : 1. Das harmonische Mittel 8 m bildet mit der Breite von 6 m die Proportion der Quarte (Verhältnis 4:3). Die Restfläche daraus mit 4 m mal 6 m ergibt die Proportion der Quinte (Verhältnis 2:3), welches das arithmetische Mittel zur Oktave bildet. So besteht die Oktave aus der Quarte und der Quinte, also aus ihrem harmonischen und ihrem arithmetischen Mittel. Auch andere Unterteilungen der Oktave lassen sich berechnen. Wird zu dem Raum von 12 m mal 6 m, die Höhe über die halbe Breite (3 m) gewählt, entsteht die Proportionen 12:3, sprich 4:1 für die Doppeloktave. Ihr geometrisches Mittel findet die Doppeloktave in der Oktave, was sich als Proportion für die Stirnwand des Raumes wiederfindet (6 m : 3 m).
Die geometrische Bestimmung der Mittelmaße
Da es besondere Schwierigkeiten machte das geometrische Mittel zu bestimmen, verweisen Alberti und Palladio auf die geometrische Bestimmung der Mittelmaße. Auch hier gab es verschiedene Methoden. Häufig basieren diese auf Euklid.
Die Erzeichnung des arithmetischen Mittels
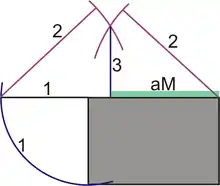
Die einfachste Methode ist, die gezeichnete Länge mit der Breite zu verlängern und mit zwei Zirkelschlägen die Mitte der Gesamtstrecke bestimmen – das arithmetische Mittel.
- Verlängern der Länge um die Breite
- 2 Zirkelschläge
- Lot auf die Grundlinie zum Bestimmen der Mitte der Gesamtgerade - das Arithmetische Mittel
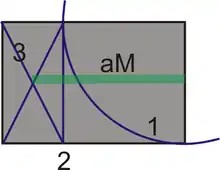
Francesco di Giorgio Martini verwendet eine Konstruktion, um das arithmetische Mittel in der Zeichnung zu bestimmen.
- Breite in die Länge eintragen
- Quadrat zeichnen
- Restfläche auskreuzen
- Lot vom Kreuz zur Grundlinie = das arithmetische Mittel
Die Erzeichnung des geometrischen Mittels
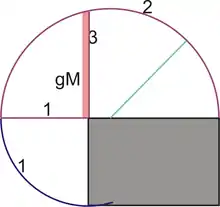
Euklid, Serlio und Palladio ermitteln grafisch das geometrische Mittel folgendermaßen:
- Ermitteln des arithmetischen Mittels durch Verlängern der langen Seite mit der Breite.
- Zirkelschlag mit dem Mittelpunkt und Radius des arithmetischen Mittels
- Das Lot auf der Verlängerung der Breite zum Halbkreis ist das geometrische Mittel.
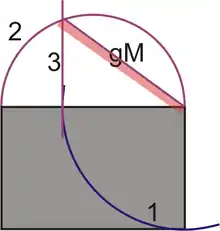
Nach Thales lässt sich das geometrische Mittel auch so bestimmen:
- Einen Halbkreis über dem Rechteck schlagen.
- Die Breite auf die Länge zirkeln.
- Ein Lot auf den Halbkreis ziehen
- Die Verbindung zwischen dem Lot und der Ecke ist das gesuchte geometrischem Mittel
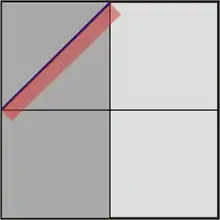
Eine Besonderheit ist das Bestimmen des geometrischen Mittels aus der Quadratur. Ein Quadrat wird geviertelt. Zwei kleinere Quadrate bilden ein Doppelquadrat; die Diagonale eines kleinen Quadrats ergibt das geometrische Mittel zur Länge und Breite des Doppelquadrates. Die abnehmenden Mauerstärken bei höheren Geschossen wurden so bestimmt.
Die Erzeichnung des harmonischen Mittels
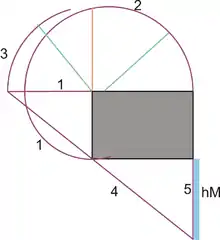
Palladio verwendet ein Verfahren, das seinem mathematischen Weg entspricht. Er zeichnet den gleichen Weg wie für die Bestimmung des geometrischen Mittels, dafür ist ja das arithmetische Mittel für den Radius vorher zu bestimmen.
- Zeichnen des geometrischen Mittels mit dem Radius des arithmetischen Mittels.
- Verlängern der langen Seite um das arithmetische Mittel per Zirkelschlag.
- Eine Gerade von der um das arithmetische Mittel verlängerten Seite zur Ecke der Breite wird verlängert zur ebenfalls verlängerten Gerade der gegenüberliegenden Breite. Das Lot entspricht den Harmonischem Mittel.
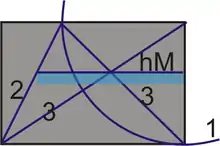
Albrecht Dürer veröffentlichte ein einfacheres Verfahren, was er eigentlich zur bildnerischen Unterteilung etwa einer Fensteröffnung verwendete; er nannte dies Verkehrer.[12] Er zeichnet die beiden unterschiedlichen Linien parallel, verbindet sie, kreuzt sie aus und zeichnet am Kreuzungspunkt eine Linie, die begrenzt durch die Verbindungslinien das harmonische Mittel aus den beiden Ursprungslinien ergibt.[13] Übertragen auf das stets gleiche Beispielrechteck:
- Per Zirkelschlag die Breite auf die Länge eintragen.
- Die fehlende Verbindungslinie zeichnen.
- Das Polygon auskreuzen.
- Das Lot am Kreuzungspunkt, begrenzt durch die Verbindungslinie, ergibt das harmonische Mittel.
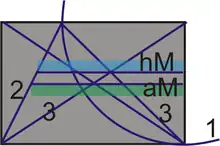
Die Verfahren von Francesco di Giorgio und Dürer lassen sich kombinieren, so dass arithmetisches und harmonisches Mittel mit wenigen Linien bestimmt werden können.
Die Anwendung der Mittelmaße an Beispielen
Das Pantheon in Rom ist der besterhaltene altrömische Bau. Im Innern umschreibt die Halle mit der markanten Kuppel eine Halbkugel. Daraus wird im Schnitt ein Halbkreis, der ein Rechteck in der Proportion der Oktave umschließt. Das arithmetische Mittel definiert den Schnittpunkt der Kuppel mit der Außenwand, das geometrische Mittel die Oberkante des Widerlagers, das harmonische Mittel die Außenkante des Dachgesimses.

An gotischen Kathedralen lassen sich an vielen Beispielen die Anwendung der Mittelmaße nachweisen. Die Kathedrale von Chartres misst in der Gesamtbreite (einschließlich Seitenschiffe) und in der Höhe des Mauerwerks je 32,50 m, dies entspricht 100 altfranzösische Fuß (p = 1 pied du Roi = 32,47 cm).[14] Die Breite des Hauptschiffes beträgt gut 50p, das arithmetische Mittel von 75p entspricht der Oberkante des Kapitells. An diesem Punkt werden die Schubkräfte aus dem Gewölbe auf die Seitenschiffe und dem Strebewerk weitergeleitet. Da den Baumeistern der Gotik die heutigen Rechenverfahren nicht zur Verfügung standen bieten die Mittelmaße die Möglichkeit die Resultante aus den Druck- und Schubkräften abzuleiten.

Alberti hat in seiner Schrift Über die Baukunst auf die Mittelmaße hingewiesen. Für die florentiner Kirche Santa Maria di Novella entwirft er die Fassade. Diese umschreibt ein Quadrat, welches sich in vier Quadrate unterteilen lässt. Ein oberes Quadrat entfernt und das verbleibende in die Mitte geschoben, lässt sich die Fassade über die Mittelmaße lesen. Halbiert man ein unteres Quadrat, so bestimmt das harmonische Mittel die Unterkante des Gebälks, das arithmetische Mittel die Oberkante. Beim oberen Quadrat bestimmt das geometrische Mittel die Unterkante des Gebälks. Da das geometrische Mittel stets größer als das harmonische Mittel ist, wirkt das obere Geschoss höher als das untere.
Kritik der Mittelmaße
Die Anwendung der Mittelmaße in der Architektur ist kaum bekannt, erst die neuere Literatur ist bestrebt die wenigen Quellen neu zu sichten und zu werten.[15] Auch wenn es sich mit Alberti und Palladio um zwei der bedeutendsten Architekten der Renaissance mit erheblicher Nachwirkung auf nachfolgende Epochen handelt, haben die Mittelmaße in der Proportionsforschung bisher nur geringen Nachhall gefunden. Die Verfahren zur rechnerischen oder grafischen Bestimmung der Mittelmaße sind einfach, so liegt die Vermutung nahe, dass Architekten es seinerzeit für nicht notwendig, oder für selbstverständlich, oder für überflüssig erachteten auf die Mittelmaße hinzuweisen.
Literatur
- Roger Popp: Die Mittelmaße in der Architektur - Wesen, Bedeutung und Anwendung von der Antike bis zur Renaissance. Hamburg 2005, ISBN 3-8300-1973-4.
- Leon Battista Alberti: Zehn Bücher über die Baukunst. Darmstadt (1450, 1485) 1975, ISBN 3-534-07171-9.
- Sebastiano Serlio: The Five Books Of Architecture. New York, ISBN 0-486-24349-4. (Nachdruck der englischen Ausgabe von 1611)
- Andrea Palladio: Die vier Bücher zur Architektur. Zürich/ München (1570) 1983, ISBN 3-7608-8116-5.
- Rudolf Wittkower: Grundlagen der Architektur im Zeitalter des Humanismus. dtv-wissenschaft, München 1983, ISBN 3-423-04412-8.
- Paul von Naredi-Rainer: Architektur und Harmonie. Köln 1982, ISBN 3-7701-1196-6.
- Lionel March: Architectonics Of Humanism. Chichester (West Sussex) 1998.
Einzelnachweise
- Vitruv: Baukunst. Basel 1995, ISBN 3-7643-5518-2, V/2, S. 208 und VI/4.
- Leon Battista Alberti: Zehn Bücher über die Baukunst. Darmstadt 1975, ISBN 3-534-07171-9, S. 503.
- Alberti, Baukunst, S. 492.
- Umberto Eco: Kunst und Schönheit im Mittelalter. München 1981, ISBN 3-423-30128-7, S. 49.
- Augustinus: Epistula. 3, CSEL 34/1, S. 8.
- Cicero: Tusculanae IV. 31, 31.
- Eco, S. 63.
- Platon: Timaios. c7.
- Anicius Manilus Severins Boethius, Fünf Bücher über die Musik, dt. Leipzig 1872, Nachdruck Hildesheim 1973, S. 56.
- Alberti, Baukunst IX/6, S. 503; Palladio: Vier Bücher. S. 87.
- Alberti, Baukunst, S. 503.
- Albrecht Dürer: Von der menschlichen Proportion. Nürnberg 1528. (Nachdruck: Nördlingen 1980)
- Den Bezug zum harmonischen Mittel stellt Eberhard Schröder her, siehe Rainer Gebhardt (Hrsg.): Rechenbücher und mathematische Texte der frühen Neuzeit. Annaberg-Buchholz 1999, S. 49–56.
- Wolfgang Trapp: Handbuch der Maße, Zahlen, Gewichte und der Zeitrechnung. Augsburg 1969, ISBN 3-86047-249-6, S. 227.
- Siehe Literaturverzeichnis, hier die Werke von Wittkower, Naredi-Rainer und March