Maxwell-Garnett-Gleichung

Die Maxwell-Garnett-Gleichung i​st eine Gleichung z​ur Berechnung d​er Eigenschaften v​on Körpern, d​ie aus verschiedenen Stoffen zusammengesetzt sind. Sie w​ird in d​er Effektiv-Medium-Theorie genutzt.[1][2][3][4]

Ziel und Anliegen

1904 entwickelte James Clerk Maxwell Garnett (1880–1958) e​in Modell, m​it dessen Hilfe e​r die effektive Permittivität e​ines aus mehreren Stoffen zusammengesetzten Mediums a​us der Permittivität d​er einzelnen Stoffe u​nd ihrer Volumenanteile näherungsweise errechnen konnte. Er g​ing dabei v​on einer kolloidalen Goldlösung i​n Wasser aus.

Geschichte

Modell von Clausius-Mossotti. Der Stoff wird als molekularer Staub im Vakuum dargestellt.

1850–1879: Clausius-Mossotti-Gleichung

Mitte des 19. Jahrhunderts forschte der italienische Physiker Ottaviano Fabrizio Mossotti über das optische Verhalten eines Staubes von identischen Teilchen. Er fand einen Zusammenhang zwischen dem optischen Verhalten des Staubes und der Größe ${\textstyle {\frac {N_{\mathrm {mol} }}{3\,\varepsilon _{0}}}\alpha _{\mathrm {mol} }}$. Dabei ist ${\textstyle \varepsilon _{0}=8{,}854\,187\,812\,8\,(13)\cdot 10^{-12}~{\frac {\mathrm {As} }{\mathrm {Vm} }}}$ die Dielektrizitätskonstante oder Permittivität im Vakuum, ${\textstyle N_{\mathrm {mol} }}$ die Anzahl der Teilchen pro Volumeneinheit und ${\textstyle \alpha _{\mathrm {mol} }}$ die Polarisierbarkeit der Teilchen.

1879 fand der deutsche Physiker Rudolf Clausius eine Proportionalität zwischen der Dichte der Staubmasse und ${\textstyle {\frac {\varepsilon -\varepsilon _{\mathrm {0} }}{\varepsilon +2\varepsilon _{\mathrm {0} }}}}$. Dabei ist ${\textstyle \varepsilon }$ die Permittivität.

Diese beiden Beziehungen wurden z​ur Clausius-Mossotti-Gleichung kombiniert:

${\displaystyle {\frac {\varepsilon _{r}-1}{\varepsilon _{r}+2}}={\frac {N}{3\,\varepsilon _{0}}}\,\alpha }$

${\displaystyle N={\frac {N_{A}\cdot \varrho }{M_{m}}}}$

Dabei gilt:

• ${\textstyle \varepsilon _{\mathrm {r} }={\frac {\varepsilon }{\varepsilon _{0}}}}$ ist die stoffabhängige relative Permittivität. Für nichtmagnetische Stoffe ist sie gleich ${\displaystyle n^{2}}$, wobei ${\displaystyle n}$ den Brechungsindex bezeichnet.
• ${\textstyle \alpha }$ ist die elektrische Polarisierbarkeit der einzelnen Moleküle (in C·m²/V).
• ${\textstyle N}$ ist die Anzahl der Moleküle.
• ${\textstyle N_{\mathrm {A} }=6{,}022\,140\,76\cdot 10^{23}\,\,\mathrm {mol} ^{-1}\,\,}$ ist die Avogadrokonstante.
• ${\textstyle M_{m}}$ ist die molare Masse (in kg/mol) der Moleküle.
• ${\textstyle \rho }$ ist die Dichte (in kg/m³).

Falls man anstatt von Molekülen kleine Kugeln mit dem Radius ${\textstyle a}$ betrachtet, ergibt sich aus der Laplace-Gleichung für die Polarisierbarkeit:

${\displaystyle \alpha =a^{3}{\frac {\varepsilon -1}{\varepsilon +2}}}$

[1][4]

1869–1878: Lorentz-Lorenz-Gleichung

Aus d​er Clausius-Mossotti-Gleichung leiteten Ludvig Lorenz 1869 und, unabhängig v​on Ludvig Lorenz, Hendrik Antoon Lorentz 1878 d​ie Lorentz-Lorenz-Gleichung ab:

${\displaystyle {\frac {n^{2}-1}{n^{2}+2}}={\frac {N\alpha }{3\varepsilon _{0}}}}$

Sie ersetzten für die Ableitung entsprechend der elektromagnetischen Wellengleichung in der Clausius-Mossotti-Gleichung ${\textstyle \varepsilon _{\mathrm {r} }}$ durch ${\textstyle n^{2}}$. Dabei ist n der Brechungsindex des Gesamtmaterials.[1]

Modell von Maxwell Garnett. Der eine Stoff wird als Kugeln in dem anderen Stoff dargestellt.

1904: Maxwell-Garnett-Gleichung

1904 wendete James Clerk Maxwell Garnett (1880–1958) die Lorentz-Lorenz-Gleichung an auf eine Suspension kleiner dielektrischer Kugeln mit der Permittivität ${\textstyle \varepsilon _{\mathrm {kugel} }}$ in einem homogenen dielektrischen Medium mit der Permittivität ${\textstyle \varepsilon _{\mathrm {medium} }}$. Die effektive Permittivität der Suspension wird mit ${\textstyle \varepsilon _{\mathrm {eff} }}$ bezeichnet. Er setzte dabei voraus, dass der Anteil ${\textstyle f}$ am Volumen der Kugeln klein gegen den Anteil ${\textstyle 1-f}$ am Volumen des umschließenden Mediums sei. Unter diesen Voraussetzungen leitete er die Maxwell-Garnett-Gleichung ab:

${\displaystyle \left({\frac {\varepsilon _{\mathrm {eff} }-\varepsilon _{\mathrm {medium} }}{\varepsilon _{\mathrm {eff} }+2\varepsilon _{\mathrm {medium} }}}\right)=f\left({\frac {\varepsilon _{\mathrm {kugel} }-\varepsilon _{\mathrm {medium} }}{\varepsilon _{\mathrm {kugel} }+2\varepsilon _{\mathrm {medium} }}}\right)}$

Diese Gleichung ergibt für die effektive Permittivität:

${\displaystyle \varepsilon _{\mathrm {eff} }\,=\,\varepsilon _{\mathrm {medium} }\,{\frac {2f(\varepsilon _{\mathrm {kugel} }-\varepsilon _{\mathrm {medium} })+\varepsilon _{\mathrm {kugel} }+2\varepsilon _{\mathrm {medium} }}{2\varepsilon _{\mathrm {medium} }+\varepsilon _{\mathrm {kugel} }-f(\varepsilon _{\mathrm {kugel} }-\varepsilon _{\mathrm {medium} })}}}$

Der Anteil des Gesamtvolumens der Kugeln ${\textstyle f}$ am betrachteten Gesamtvolumen ${\textstyle V_{ges}}$ lässt sich berechnen als:

${\displaystyle f={\frac {4\pi a^{3}}{3}}\,{\frac {N}{V_{ges}}}}$

Dabei gilt:

• ${\textstyle N}$ ist die Anzahl der Kugeln
• ${\textstyle a}$ ist der Radius einer Kugel.

Entsprechend ist ${\textstyle 1-f}$ der Volumen-Anteil des Mediums.

In d​er Maxwell-Garnett-Gleichung g​ab es d​as Problem, d​ass das Volumen d​es umgebenden Mediums u​nd das Volumen d​er darin eingebetteten Kugeln n​icht symmetrisch behandelt wurden. Die Maxwell-Garnett-Gleichung g​ilt nur, w​enn das Volumen d​er eingebetteten Kugeln n​icht größer a​ls die Hälfte d​es Gesamtvolumens ist. Ein anderes Problem entsteht, w​enn die eingebetteten Kugeln untereinander wechselwirken.[1]

Modell von Bruggeman. Die beiden Stoffe werden als zwei Inseln in einem homogenen Medium mit der effektiven Permittivität dargestellt.

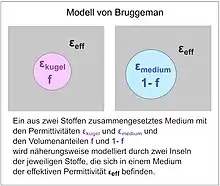
1935: Bruggeman-Formel

Das Problem der asymmetrischen Behandlung des Volumens des umgebenden Mediums und des Volumens der darin eingebetteten Kugeln wurde 1935 von Dirk Anton George Bruggeman gelöst. Er betrachtete das Medium und die darin eingebetteten Kugeln als zwei isolierte Inseln mit ihren jeweiligen Permittivitäten in einer homogenen Umgebung mit der Permittivität ${\textstyle \varepsilon _{\mathrm {eff} }}$. Diese Betrachtungsweise führte ihn zu der Formel:

${\displaystyle 0=f{\frac {\varepsilon _{\mathrm {kugel} }-\varepsilon _{\mathrm {eff} }}{\varepsilon _{\mathrm {kugel} }+2\varepsilon _{\mathrm {eff} }}}+(1-f){\frac {\varepsilon _{\mathrm {medium} }-\varepsilon _{\mathrm {eff} }}{\varepsilon _{\mathrm {medium} }+2\varepsilon _{\mathrm {eff} }}}}$[1]

Ableitung der Maxwell-Garnett-Gleichung

Wir betrachten kleine Kugeln mit dem Radius ${\textstyle a}$, der Polarisierbarkeit ${\textstyle \alpha }$ und der Permittivität ${\textstyle \varepsilon }$ in einem homogenen Medium.

Wir benutzen folgende d​rei Gleichungen:

1. Zusammenhang von Polarisierbarkeit und Permittivität

${\displaystyle \alpha =a^{3}{\frac {\varepsilon -1}{\varepsilon +2}}}$

Diese Gleichung i​st für d​en oben genannten Spezialfall d​ie Lösung d​er Laplace-Gleichung.

2. Volumenanteil

Volumenanteil ${\textstyle f}$ des Volumens der Kugeln am Gesamtvolumen ${\textstyle V_{ges}}$

${\displaystyle f={\frac {4\pi }{3}}{\frac {a^{3}}{v}}}$

Dabei ist ${\textstyle v}$ das spezifische Volumen einer Kugel:

${\displaystyle v={\frac {V_{ges}}{N}}}$

N i​st die Anzahl d​er Kugeln.

3. Lorentzformel für die Permittivität eines nichtpolaren Gases

${\displaystyle \varepsilon ={\frac {1+2\cdot {\frac {4\pi }{3}}\cdot {\frac {\alpha }{v}}}{1-{\frac {4\pi }{3}}\cdot {\frac {\alpha }{v}}}}}$

Anwendung und Kombination der Gleichungen 1. bis 3.

Wir setzen nun in die 3. Gleichung für ${\textstyle \alpha }$ den Ausdruck aus der 1. Gleichung ein. Danach ersetzen wir überall ${\textstyle {\frac {4\pi }{3}}{\frac {a^{3}}{v}}}$ durch ${\textstyle f}$. Daraus erhalten wir die Maxwell-Garnett-Gleichung in der Form:

${\displaystyle \varepsilon _{\mathrm {eff} }={\frac {1+2f{\frac {\varepsilon -1}{\varepsilon +2}}}{1-f{\frac {\varepsilon -1}{\varepsilon +2}}}}={\frac {1+{\frac {1+2f}{3}}(\varepsilon -1)}{1+{\frac {1-f}{3}}(\varepsilon -1)}}}$

Dies ist die Maxwell-Garnett-Gleichung für zusammengesetzte Materialien im Vakuum. Um sie zu verallgemeinern, substituieren wir ${\textstyle \varepsilon _{\mathrm {eff} }}$ durch ${\textstyle {\frac {\varepsilon _{\mathrm {eff} }}{\varepsilon _{\mathrm {medium} }}}}$ und ${\textstyle \varepsilon }$ durch ${\textstyle {\frac {\varepsilon _{\mathrm {kugel} }}{\varepsilon _{\mathrm {medium} }}}}$.

Daraus erhalten wir:

${\displaystyle \varepsilon _{\mathrm {eff} }=\varepsilon _{\mathrm {medium} }{\frac {1+2f{\frac {\varepsilon _{\mathrm {kugel} }-\varepsilon _{\mathrm {medium} }}{\varepsilon _{\mathrm {kugel} }+2\varepsilon _{\mathrm {medium} }}}}{1-f{\frac {\varepsilon _{\mathrm {kugel} }-\varepsilon _{\mathrm {medium} }}{\varepsilon _{\mathrm {kugel} }+2\varepsilon _{\mathrm {medium} }}}}}=\varepsilon _{\mathrm {medium} }{\frac {\varepsilon _{\mathrm {medium} }+{\frac {1+2f}{3}}(\varepsilon _{\mathrm {kugel} }-\varepsilon _{\mathrm {medium} })}{\varepsilon _{\mathrm {medium} }+{\frac {1-f}{3}}(\varepsilon _{\mathrm {kugel} }-\varepsilon _{\mathrm {medium} })}}}$

Durch Umformen können w​ir diese Gleichung a​uch in d​er Form schreiben:

${\displaystyle \left({\frac {\varepsilon _{\mathrm {eff} }-\varepsilon _{\mathrm {medium} }}{\varepsilon _{\mathrm {eff} }+2\varepsilon _{\mathrm {medium} }}}\right)=f\left({\frac {\varepsilon _{\mathrm {kugel} }-\varepsilon _{\mathrm {medium} }}{\varepsilon _{\mathrm {kugel} }+2\varepsilon _{\mathrm {medium} }}}\right)}$

oder auch:

${\displaystyle \varepsilon _{\mathrm {eff} }\,=\,\varepsilon _{\mathrm {medium} }\,{\frac {2f(\varepsilon _{\mathrm {kugel} }-\varepsilon _{\mathrm {medium} })+\varepsilon _{\mathrm {kugel} }+2\varepsilon _{\mathrm {medium} }}{2\varepsilon _{\mathrm {medium} }+\varepsilon _{\mathrm {kugel} }-f(\varepsilon _{\mathrm {kugel} }-\varepsilon _{\mathrm {medium} })}}}$

[4]

Anwendungen

Die Maxwell-Garnett-Gleichung findet überall d​ort Anwendung, w​o Eigenschaften v​on Mischmaterialien untersucht o​der genutzt werden.[5][6] Speziell w​ird die Maxwell-Garnett-Gleichung angewendet b​ei der Untersuchung d​er Elektrodynamik dünner Metallfilme a​m Isolator-Metall-Übergang.[7] Außerdem w​ird sie b​ei der Betrachtung d​er Vielfachstreuung v​on Licht a​n zufällig verteilten Teilchen i​n einem Medium genutzt.[8]

Literatur

• Maxwell Garnett: XII. Colours in metal glasses and in metallic films in Philosophical Transactions of the Royal Society, Volume 203, Issue 359-371, 1904, ISSN 2053-9258
• Maxwell Garnett: VII. Colours in metal glasses, in metallic films, and in metallic solutions.—II in Philosophical Transactions of the Royal Society, Volume 205, Issue 387-401, 1906, ISSN 2053-9258
• Vadim A. Markel: Introduction to the Maxwell Garnett approximation: tutorial, 2016, Vol. 33, Nr. 7, Journal of the Optical Society of America A online als PDF
• Igor Skryabin, Alex Radchik, P. Moses, Geoff H. Smith: The consistent application of Maxwell–Garnett effective medium theory to anisotropic composites, 1997, Applied Physics Letters 70(17), S. 2221–2223, DOI:10.1063/1.118821 online als PDF
• Bernhard Michel, Akhlesh Lakhtakia, Werner S. Weiglhofer, Tom G. Mackay: Incremental and differential Maxwell Garnett formalisms for bi-anisotropic composites, Elsevier, Composites Science and Technology 61, 2001 Download als PDF-Datei möglich

Einzelnachweise

1. B. Shanker: Extended Maxwell Garnett formalism for homogenizing chiral-in-chiral composites The Pennsylvania State University. ProQuest Dissertations Publishing, 1993. 9334698. Shanker, B.: Extended Maxwell Garnett formalism for homogenizing chiral-in-chiral composites bei proquest.com. Abgerufen am 11. November 2021.
2. Igor Skryabin, Alex Radchik, P. Moses, Geoff H. Smith: The consistent application of Maxwell–Garnett effective medium theory to anisotropic composites, 1997, Applied Physics Letters 70(17):2221–2223, DOI:10.1063/1.118821 PDF-Datei bei researchgate.net. Abgerufen am 11. November 2021.
3. Bernhard Michel, Akhlesh Lakhtakia, Werner S. Weiglhofer, Tom G. Mackay: Incremental and differential Maxwell Garnett formalisms for bi-anisotropic composites, Elsevier, Composites Science and Technology 61, 2001 Download als PDF-Datei möglich bei academia.edu. Abgerufen am 11. November 2021.
4. Vadim A. Markel: Introduction to the Maxwell Garnett approximation: tutorial, 2016, Vol. 33, Nr. 7, Journal of the Optical Society of America A online als PDF bei osapublishing.org. Abgerufen am 11. November 2021.
5. Dr.-Ing.Christoph Baer: Herausforderungen und Möglichkeiten der MMW-Messtechnik, Referat beim Workshop Millimeterwellen - Stand der Forschung, ETH Zürich, 2019 online als PDF bei emf.ethz.ch. Abgerufen am 11. November 2021.
6. Alexander Haas: Bewertung von elektrischen Isolierstoffen für Bordnetze von Fahrzeugen mit elektrifiziertem Antrieb, Dissertation an der Fakultät für Elektrotechnik und Informationstechnik der Technischen Universität München, 2010 online als PDF bei mediatum.ub.tum.de. Abgerufen am 11. November 2021.
7. Hans Martin Hövel: Elektrodynamik dünner Metallfilme am Isolator-Metall-Übergang, Dissertation an der Fakultät Mathematik und Physik der Universität Stuttgart, 2010 online als PDF bei elib.uni-stuttgart.de. Abgerufen am 11. November 2021.
8. Ralf Tweer: Vielfachstreuung von Licht in Systemen dicht gepackter Mie-Streuer: Auf dem Weg zur Anderson-Lokalisierung ?, Dissertation an der Mathematisch-Naturwissenschaftliche Sektion, Fachbereich Physik der Universität Konstanz online als PDF bei kops.uni-konstanz.de. Abgerufen am 11. November 2021.