Kutzbachplan
Der Kutzbachplan ist ein graphisches Verfahren, mit dem die Drehzahlen und Drehrichtungen aller Räder in einem Zahnradgetriebe bestimmt werden können. Bei Umkehr des Verfahrens lassen sich die Abmessungen der Räder bei vorgegebenem Übersetzungsverhältnis ermitteln.[1]
Entwickelt wurde dieses Verfahren von Karl Kutzbach, der seit 1913 als Professor an der TH Dresden Zahnradgetriebe erforschte und weiterentwickelte. Es wird vorteilhaft bei Planetengetrieben angewendet, bei denen die Verhältnisse im Gegensatz zu Standgetrieben weniger leicht überblickbar sind.[1]
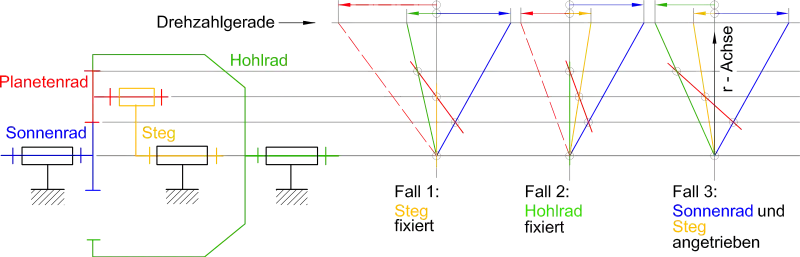
Verfahren
In radialer Richtung der Räder (r-Achse) werden ihre Umfangsgeschwindigkeiten aufgetragen. Es sind Geraden (sogenannte Seilstrahlen), denn die Umfangsgeschwindigkeit u an einem Rad wächst linear mit dem Radius r. Die Drehzahlen der Räder sind der Neigung ihrer Seilstrahlen gegenüber der r-Achse proportional. Gegensätzliche Richtung der Neigung bedeutet gegensätzliche Drehrichtung.
- Die Seilstrahlen von im Gestell gelagerten Rädern schneiden die r-Achse an den Stellen ihrer Drehachse (u=0).
- Die Seilstrahlen zweier Räder schneiden sich dort, wo sie miteinander kämmen. r-Werte und Umfangsgeschwindigkeiten sind gleich. Die Drehrichtungen sind gegensätzlich.
Dieser Teil des Kutzbachplans ist der sogenannte Geschwindigkeitsplan.
Untersuchung eines vorgegebenen Getriebes
Im Fall 1 in obiger Abbildung ist der Steg (gelb) fixiert, das heißt dem Gestell zugefügt. Es ist ein gewöhnliches Standgetriebe entstanden. Der Seilstrahl des Stegs fällt mit der r-Achse zusammen. Das Sonnenrad (blau) sei angetrieben. Seine Drehgeschwindigkeit wird mit dem blauen Seilstrahl beliebig gewählter Neigung dargestellt. Das Planetenrad (rot) kämmt mit dem Sonnenrad, schneidet dessen Seilstrahl folglich an der entsprechenden Stelle auf der r-Achse. Seine Drehachse ist zusammen mit dem Steg fixiert, und sein Seilstrahl hat dort eine Nullstelle, die der zweite ihn bestimmende Punkt ist. Seine Verlängerung zum Wälzradius des Hohlrades (grün), mit dem es kämmt, ergibt einen Punkt für dessen Seilgerade. Die Verbindung von dort zum Schnitt der Drehachse des Hohlrades mit der r-Achse ist dessen Seilgerade. Wird das Hohlrad oder das Planetenrad angetrieben, so zeichnet man zuerst dessen Seilgerade und erhält als Ergebnis wieder die Seilgeraden der beiden anderen Räder.
Die Drehzahl- und Drehrichtungs-Verhältnisse werden auf einer Senkrechten zur r-Achse (in der Abbildung Drehzahlgerade genannt) dargestellt. Diese wird von den Seilstrahlen geschnitten, die alle von einem Punkt ausgehen müssen. Für das Planetenrad ist eine Parallele durch den sonst gemeinsamen Schnittpunkt gezeichnet (Strahlensatz). Dieser Teil des Kutzbachplans ist der sogenannte Drehzahlplan.
Der besondere Vorteil des Kutzbachplanes wird bei rotierendem Steg und umlaufenden Planetenrädern eines Planetenradgetriebes evident. Sonnen- oder Hohlrad werden festgehalten. Im Fall 2 in obiger Abbildung ist das Hohlrad fixiert. Sonnenrad oder Steg sind angetrieben, und Steg oder Sonnenrad sind das getriebene Teil.
Darstellbar sind auch die Verhältnisse, wenn alle Teile drehen. Zwanglauf herrscht dann nur, wenn zwei der drei im Gestell drehbaren Teile angetrieben sind, das dritte ist das getriebene Teil. Im Fall 3 in obiger Abbildung werden beispielsweise Sonnenrad und Steg angetrieben, und die Drehung des Hohlrades ergibt sich daraus. Der Plan sieht prinzipiell gleich aus, wenn Sonnenrad und Hohlrad oder Steg und Hohlrad angetrieben werden.
Dimensionierung eines Getriebes
Zu bestimmen sind die Wälzkreisdurchmesser der Räder (und die davon abhängigen Achsabstände) bei vorgegebenem Übersetzungsverhältnis (beziehungsweise bei vorgegebenen Drehzahlen der ins Verhältnis eingehenden beiden Räder).
Die Drehzahlen werden auf der Drehzahlgerade als Vektoren aufgetragen und mit ihnen der Drehzahlplan erstellt. Mit Hilfe der darin entstandenen Seilstrahlen wird anschließend der Geschwindigkeitsplan gezeichnet. Einige der geometrischen Größen sind vorzugeben, alle anderen sind damit bestimmt, das heißt, sie ergeben sich aus dem Geschwindigkeitsplan. Sollte das entstandene Getriebe nicht als zweckmäßig erachtet werden, sind die Vorgaben zu ändern und ein neuer Plan zu zeichnen.
Im Beispiel von Fall 1 in der Abbildung sei ein bestimmtes Verhältnis zwischen der Drehzahl des Sonnenrades und der des Hohlrades zu verwirklichen. Werden zum Beispiel der Wälzkreisdurchmesser des Sonnenrades und die Achslage des Planetenrades auf dem Steg vorgegeben, erhält man die Wälzkreisdurchmesser des Hohlrades und des Planetenrades. Dabei zeichnet man den Seilstrahl des Planetenrades.
Swampsches Schema
Für die genaue Bestimmung der Drehzahlen und Geschwindigkeiten reicht der Kutzbachplan wegen der begrenzten Zeichengenauigkeit nicht aus. Die mit ihm dargestellten geometrischen Verhältnisse sind eindeutig und demzufolge rechnerisch genau erfassbar. Man kann sich dazu eines zusammenfassenden rechnerischen Schemas von Swamp bedienen.[2][3]
Einzelnachweise
- Siegfried Hildebrand: Feinmechanische Bauelemente, Hanser 1968, Seite 543
- Hildebrand, S. 546
- TU Dresden, Institut für Maschinenelemente: Antriebselemente, Formelsammlung