Kugelkondensator
Unter einem Kugelkondensator oder sphärischen Kondensator[1] versteht man einen elektrischen Kondensator, der aus zwei konzentrischen, gegeneinander isolierten, metallischen Kugeloberflächen besteht.
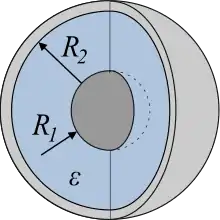
Für die Kapazität eines Kugelkondensators mit den Radien und gilt
- , mit
ε0 ist hierbei die elektrische Feldkonstante. εr ist die Dielektrizitätszahl, welche im Vakuum gleich 1 ist.
Herleitung der Formel für die Kapazität
Für eine infinitesimal kleine Kugelschale zwischen R1 und R2 gilt für das infinitesimal kleine Reziproke der Kapazität der bekannte Zusammenhang des Plattenkondensators:
wobei A(r) die Oberfläche einer Kugel ist. Integriert man nun, so ergibt sich:
Umgestellt nach der Kapazität C ergibt dies oben genannte Formel.
Alternativ lässt sich auch die Definition nutzen, wenn man die Formel im Abschnitt Spannung zwischen innerer und äußerer Platte verwendet.
Sonderfälle
Sehr kleiner Abstand
Wenn , kann man angenähert setzen und erhält .
Sehr großer Abstand

Wenn ist, kann man angenähert setzen und erhält . Die Kapazität wird dann praktisch nur vom Radius der Innenkugel bestimmt.
Diese Näherung beschreibt auch die Kapazität einer freistehenden Kugel (auch als Kugelelektrode[1] bezeichnet), da hier die Gegenelektrode sehr weit entfernt ist ( und somit ). Der Radius einer solchen Kugelelektrode im Vakuum diente früher als Maßeinheit der Kapazität mit folgender Äquivalenz:
Ladung und Ladungsdichte
Beim Kugelkondensator geht man davon aus, dass die beiden Elektroden mit der Ladung und entgegengesetzt geladen sind. Diese Ladungen befinden sich als Flächenladungen auf den nach innen gewandten Kugelflächen. Dann lässt sich die Ladungsdichte schreiben als , wobei die Dirac'sche Delta-Distribution ist.
Elektrisches Feld
Der Vektor des elektrischen Feldes zwischen den zwei Kondensatorschalen besteht wegen der Kugelsymmetrie nur aus der radialen Komponente . Diese lässt sich mit der folgenden Formel berechnen:
- wobei
Das Feld ist nicht homogen, sondern abhängig vom Abstand zum Mittelpunkt des Kondensators. Innerhalb der Elektroden und außerhalb des Kondensators ist kein elektrisches Feld vorhanden.
Elektrisches Potential
Das elektrische Potential ist ein nur von abhängiges Skalarfeld und berechnet sich, bis auf eine additive Konstante, als . Dieses Integral kann abschnittsweise ermittelt werden:
- Für ist .
- Für ist .
- Für ist .
Spannung zwischen innerer und äußerer Platte
Die Spannung zwischen der inneren und äußeren Kugel berechnet sich wie folgt:
Literatur
- Eugen Philippow (Hrsg.): Taschenbuch Elektrotechnik, Band 1. Verlag Technik, Berlin 1968, DNB 365695874, S. 308 ff.
- Klaus Lunze: Einführung in die Elektrotechnik: Leitfaden und Aufgaben Teil I: Elektrische Kreise bei Gleichstrom und das elektrische Feld. 3. Auflage. Verlag Technik, Berlin 1964, DNB 453110886, S. 181 ff.
Einzelnachweise
- Eugen Philippow: Grundlagen der Elektrotechnik. Akademische Verlagsgesellschaft Geest&Portig K.-G., Leipzig 1967, DNB 457803371, S. 82 ff.