Kronig-Penney-Modell
Beim Kronig-Penney-Modell (nach Ralph Kronig und William Penney) handelt es sich um ein einfaches Modell der Festkörperphysik, das das Verhalten von Valenzelektronen in kristallinen Festkörpern erklärt. Aus ihm ergibt sich eine Bandstruktur der Energie, wie sie ähnlich auch in der Natur auftritt, zum Beispiel bei Metallen und Halbleitern.
Erklärung
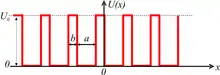
Das eindimensionale Modell geht von einer Aneinanderreihung von Potentialtöpfen der Tiefe U0 aus, die jeweils a breit und durch eine Barriere der Breite b getrennt sind. Die Töpfe stellen den Bereich in der Nähe der Atomkerne dar, in dem die Elektronen von der Kernladung angezogen werden. Die Barrieren entsprechen den zwischen den Kernen liegenden Gebieten, in denen die Ladung der Kerne durch die der kernnahen Elektronen abgeschirmt ist. Das Gitter ist unendlich ausgedehnt, und nach dem Bloch-Theorem ergeben sich räumlich periodische Lösungen der Schrödinger-Gleichung. Setzt man diese Voraussetzungen an, so ergeben sich Energiebänder, die durch verbotene Energiebereiche getrennt sind. Es können keine Elektronen mit Energien aus den verbotenen Bereichen im Kristall existieren, nur mit Energien aus den Energiebändern.
An der Grenze zwischen erlaubten und verbotenen Energiebereichen bilden sich auf Grund von Bragg-Reflexion stehende Wellen aus. Diejenigen stehenden Wellen, bei denen sich die Elektronen bevorzugt in der Nähe von Atomkernen aufhalten, sind energetisch günstiger als jene, bei denen sich die Elektronen bevorzugt zwischen Atomkernen aufhalten. Die Bragg-Reflexion am periodischen Potenzial kann daher als Ursache der verbotenen Energiebereiche betrachtet werden[1].
Für die explizite Bandabstand-Berechnung sowie die Niveauaufteilung für das eindimensionale Penney-Kronig-Modell siehe Müller-Kirsten.[2]
Literatur
- R. de L. Kronig, W. G. Penney: Quantum Mechanics of Electrons in Crystal Lattices. In: Proceedings of the Royal Society of London. Series A. Band 130, Nr. 814, 2. März 1931, S. 499–513, doi:10.1098/rspa.1931.0019.
Einzelnachweise
- N. F. Mott, H. Jones: The Theory of the Properties of Metals and Alloys. Clarendon Press, 1936 (Dover Publ. Reprint, 1958), S. 63.
- H. J. W. Müller-Kirsten: Introduction to Quantum Mechanics: Schrödinger Equation and Path Integral. 2nd ed. World Scientific, 2012, ISBN 978-981-4397-74-2, S. 458–477 und 325–329.