Konventionalismus

Der Konventionalismus (latein. conventio: „übereinkommen“) ist innerhalb der Philosophie eine Richtung, die von der These ausgeht, dass wissenschaftliche Erkenntnisse und Gesetze (auch moralische Gesetze) nicht auf Übereinstimmung mit der Beschaffenheit der Realität, sondern auf Konventionen beruhen.

Konventionalismus als Strömung der Wissenschaftstheorie geht davon aus, dass Beobachtungstatsachen durch beliebige alternative Konstruktionen in eine rationale Ordnung gebracht werden können. Auch sich widersprechende Theorien können so immer mit den Beobachtungen in Übereinstimmung gebracht werden; demzufolge können Tatsachen keine Prüfungsinstanz für die Gültigkeit von Theorien abgeben. Erforderlichenfalls wird der Konventionalist die angestrebte Übereinstimmung mittels Einführung von Ad-hoc-Hypothesen erzielen.[1]

„Die konventionalistisch aufgefaßten Naturgesetze sind durch keine Beobachtung falsifizierbar, denn erst sie bestimmen, was eine Beobachtung, was insbesondere eine wissenschaftliche Messung ist.“

– Karl Popper: Logik der Forschung[2]

Begründung des Konventionalismus

Als Begründer des Konventionalismus gilt der französische Mathematiker und Physiker Henri Poincaré. In seinem Buch La science et l'hypothèse beschrieb er ein gedankliches Experiment zur Demonstration der „Unbestimmtheit“ der Geometrie des Raumes.

Er stellt sich eine zweidimensionale Scheibenwelt vor, auf der alle Dinge auf Grund einer universellen Kraft gleichermaßen im Abstand vom Mittelpunkt zu schrumpfen beginnen, also kleiner sind, je weiter sie vom Mittelpunkt entfernt sind. Die Bewohner dieser Welt nehmen also eine andere Geometrie des Raumes an, als für Außenstehende zu beobachten ist. Dies führt zu zwei möglichen Geometrieannahmen: die der euklidischen und der Bolyai-Lobatschewski-Geometrie. Der Konventionalismus betont, dass eine Entscheidung für eine der Theorien getroffen und als Konvention angenommen werden muss, obwohl beide Theorien gleichwertig sind und sich sogar widersprechen. Die eine Theorie ist nicht richtiger als die andere, sie ist nur bequemer (plus commode).[3]

In Bezug auf die euklidische Geometrie bedeutet dies, dass sich zum Beispiel die Maßstäbe von Objekten zueinander nicht ändern und sich Lichtstrahlen geradlinig ausbreiten, obwohl andere Modelle vorstellbar sind und nicht den Beobachtungen widersprechen; sie würden lediglich nicht unseren Konventionen und Gedankenmodellen entsprechen. Synthetische geometrische Erkenntnisse a priori im Sinne Kants seien daher nicht möglich. In Bezug auf die Arithmetik und Logik ist Poincaré jedoch der Auffassung, dass deren Aussagen a priori und notwendig sind, was von radikaleren Konventionalisten wie Rudolf Carnap bestritten wird. Noch radikalere Positionen vertraten Édouard Le Roy, für den bereits das, was wir Wirklichkeit nennen, durch Definitionen konstituiert wird, die den Phänomenen in einem „Ozean der Bilder“ Namen geben,[4] sowie Percy Williams Bridgman und Hugo Dingler mit ihrer Theorie des Operationalismus, wonach die Bedeutung eines Begriffs nichts anderes ist als eine Folge von Messoperationen, die ihn beschreibt.

Poincarés Geometrie der Scheibenwelt

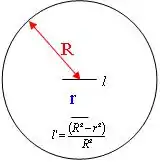
Sei Flatland eine zweidimensionale Scheibe mit dem festen Radius $R$ (somit besitzt diese konstruierte Welt eine endliche Ausdehnung). Des Weiteren soll eine universelle Kraft existieren, die dazu führt, dass alle Objekte auf dieser Scheibe mit zunehmender Entfernung vom Mittelpunkt $M$ zu schrumpfen beginnen. Dieser Schrumpfprozess folgt dabei folgendem Gesetz: Ein Objekt mit der ‚wahren‘ Länge $l$ im Zentrum hat im Abstand $r$ von $M$ die Länge $l'=l\cdot {\tfrac {R^{2}-r^{2}}{R^{2}}}$ . Diese Gesetzmäßigkeit gilt für alles, unabhängig von Material, Form etc. Damit ist die verursachende Kraft für die Flatlander nicht erfahrbar oder nachweisbar, da sie und mögliche Messgeräte (z. B. eine Schnur oder ein Messrad) gleichermaßen schrumpfen.

Bestimmung des Radius

Wenn die Flatlander nun versuchen wollten, den Radius zu bestimmen, indem sie eine Schnur benutzen, die in $M$ die Länge $l$ hat, so würden sie dabei Folgendes feststellen: Einerseits würde diese Schnur am Rand ( $r=R$ ) der Scheibe die Länge $l'=l\cdot {\tfrac {R^{2}-r^{2}}{R^{2}}}=0$ haben, andererseits könnten sie niemals den Rand erreichen, da die Summe jeder endlichen Anzahl von Messschritten – als Summe der geschrumpften Längen – stets kleiner wäre als $R$ . Somit kämen sie zu der für sie „richtigen“ Schlussfolgerung, dass ihre Welt eine unendliche Ausdehnung besitzt.

Bestimmung der Geometrie

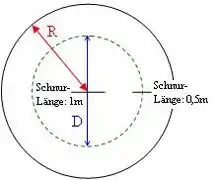
Um die Geometrie des Raumes zu bestimmen, gibt es eine einfache Möglichkeit: Man bestimmt das Verhältnis von gemessenem Umfang zu gemessenem Durchmesser eines Kreises. Wenn dieses Verhältnis gleich $\pi$ ist, handelt es sich um euklidische Geometrie, wenn es größer als $\pi$ ist, um BL-Geometrie.

Die Flatlander vermessen nun einen Kreis $k$ , dessen Mittelpunkt in $M$ liegen soll und dessen wirklicher Durchmesser $D$ so gewählt ist, dass die Größe eines Objektes (in diesem Fall die Messschnur) auf dieser Kreislinie konstant genau der Hälfte entspricht, die es in $M$ hat. Den Umfang $c$ , den sie erhalten würden, ist somit genau doppelt so groß wie der wirkliche Umfang $C$ . Bei der Messung des Durchmessers entspricht die Länge der Messschnur aber nur genau auf der Kreislinie, also am Anfang und am Ende der Messung, genau der Hälfte. In dem Bereich dazwischen ist sie immer größer als die Hälfte. Somit ist der gemessene Durchmesser $d$ weniger als doppelt so groß wie der wirkliche Durchmesser $D$ . Daraus folgt nun für das Verhältnis von $c$ zu $d$ , dass die Flatlander zu dem Resultat von ${\frac {c}{d}}>\pi$ gelangt wären und daraus konsequenterweise schließen würden, dass ihrer Welt eine Bolyai-Lobatschewski-Geometrie zugrunde liegt. Dieses Ergebnis widerspricht aber der Tatsache, dass es sich bei ihrer Welt tatsächlich um eine Scheibe in der euklidischen Ebene handelt.

Ziel des Gedankenexperiments

Mit diesem Gedankenexperiment wollte Poincaré zeigen, dass erst die Kombination aus Geometrie und Physik Beobachtungen vorhersagen kann. Dies folgt aus der Annahme, dass eine Geometrie als solche keine Vorhersage über die Welt machen kann. Passt nun das Ergebnis eines Versuchs nicht zu der dazugehörigen Vorhersage, so muss also entweder die Geometrie oder die Physik geändert werden, damit eine Übereinstimmung erzielt werden kann. Ist die Geometrie eines Raumes per Konvention festgelegt worden, so muss die Physik (also das Experiment bzw. die Messmethode) geändert werden. Kann nun der Bewohner dieser Scheibenwelt nicht erkennen, dass alle Dinge schrumpfen, sobald sie sich vom Zentrum entfernen, so ist seine Messmethode falsch, nicht aber die Geometrie an sich. Der Flatlander könnte z. B. den Satz des Pythagoras einfach dadurch widerlegen, dass er die Längenmessung der Seiten eines Dreiecks an verschiedenen Orten durchführen muss. Doch dann ist nicht der Satz des Pythagoras falsch, sondern es muss eine äußere Kraft wirken, die die Längenmessung beeinflusst. Diese muss universell sein, das heißt, dass sie alle Dinge, egal wie sie beschaffen sind und welche Eigenschaften sie haben, in gleicher Weise beeinflusst. Sie ist also für die Bewohner dieser Welt nicht nachweisbar. Daran kann man sehen, dass die Physik geändert werden kann (durch Einführung einer universellen Kraft), die Geometrie jedoch nicht. Und somit interpretieren wir auch unsere Beobachtungen stets so, dass sie mit der Geometrie übereinstimmen. Poincaré ist der festen Überzeugung, dass durch ein Experiment nicht die wahre Geometrie eines Raumes erkannt werden kann, sondern dass es lediglich aufzeigt, welche zu den gegebenen Umständen am besten passt.

Verschiedene Sichtweisen

Es gibt zwei gleichberechtigte Möglichkeiten, die geometrischen Verhältnisse auf dieser Welt zu erklären:

Die euklidische Geometrie gilt, die Objekte schrumpfen.
Die Bolyai-Lobatschewski-Geometrie gilt, die Objekte haben konstante Längen.

Daraus folgt, dass jede Geometrie als gültig erachtet werden kann, wenn nur die Annahmen (hier: Objekte schrumpfen bzw. schrumpfen nicht) entsprechend gewählt werden. Auch wir selbst sind in der gleichen Lage wie die Scheibenweltbewohner. Auch wir können nicht sagen, durch welche Geometrie sich unser Raum, in dem wir leben, wirklich beschreiben lässt. Wir können lediglich sagen, dass die euklidische Geometrie zu unseren Beobachtungen passt. Es ist jedoch reine Konvention, dass diese Geometrie gilt.

Allgemeine Interpretation

Allgemein kann also festgestellt werden, dass die Experimente und damit zusammenhängenden Beobachtungen zwei Interpretationen zulassen:

Realistische Interpretation: Die Geometrie eines Raumes ist bestimmt, jedoch können wir sie nicht erkennen, da immer irgendwelche universellen und somit auch nicht nachweisbaren Kräfte wirken können, die die Geometrie des Raumes anders sein lassen, als wir sie wahrnehmen.
Anti-realistische Interpretation: Die Geometrie eines Raumes ist unbestimmt. Das heißt, es gibt keine objektive Geometrie, die als die wahre gilt. Alle Geometrien sind somit gleich wahr.

Es stellt sich also die Frage, ob die Suche nach der wahren Geometrie ein epistemologisches oder ontologisches Problem ist. Existiert also eine wahre Geometrie, die wir nur nicht erkennen können, mit der sich jedoch alle Beobachtungen erklären lassen, oder gibt es letztendlich vielleicht doch gar keine realen Tatsachen, auf deren Grundlage eine wahre Geometrie gefunden werden kann?

Beispiel zur Interpretation

Angenommen, man mäße die Winkelsumme eines Dreiecks mit optischen Mitteln und würde beobachten, dass sie nicht 180° ergäbe. Nun gibt es zwei mögliche Interpretationen:

Realistische Interpretation: Behalt die euklidische Geometrie und mache die Annahme, dass sich die Lichtstrahlen nicht geradlinig ausbreiten.
Anti-realistische Interpretation: Behalt die Annahme, dass sich Lichtstrahlen geradlinig ausbreiten, und verwirf die euklidische Geometrie.

Aus diesen beiden Interpretationsmöglichkeiten ergibt sich also, dass wir an sich gar nicht sagen können, was richtig ist. Beide Interpretationen widersprechen nicht den Beobachtungen. Doch geht man nun davon aus, dass Physik veränderbar ist und die einfachste Geometrie (in diesem Fall die euklidische) angenommen wird, würde man sich für die erste Interpretationsmöglichkeit entscheiden.

Weiteres Beispiel

Am Beispiel seiner Deutung der Relativitätstheorie, die Poincaré mitentwickelte, lässt sich sein Konventionalismus vielleicht besonders provokant illustrieren: Verkürzen sich bei sehr schnellen Bewegungen nur die Lineale oder auch die Geometrie? „Fließt“ ein durch das Gravitationsfeld der Sonne abgelenkter Lichtstrahl durch den gekrümmten Raum oder bleibt der Raum „gerade“? Poincaré gibt als Antwort: Es ist Konvention! Die relativistische Krümmung ist nämlich nur als Krümmung der Lichtstrahl-Geodäte – etwa dadurch, dass sie durch ein Gravitationsfeld abgelenkt wird – auffassbar und nicht notwendig als Krümmung einer geometrischen Geraden. Die „Metriken“ der Feldgleichungen sind also nicht zwingend geometrische Metriken (vgl. Hinweise zur Diskussion Protophysik vs. Relativitätstheorie in Protophysik). Insofern bleibt die Frage, ob die wirkliche Geometrie euklidisch oder nichteuklidisch ist, für den Konventionalisten Poincaré offen.

Die Konventionalismus-Kritik von Karl Popper

Für Karl Popper ist Konventionalismus als Wissenschaftstheorie logisch und praktisch immer durchführbar. Denn der Konventionalist kann im Fall einer „Krise der Wissenschaft“ stets die Beobachtungen durch Änderung der Messverfahren uminterpretieren.[5]

Dies entspricht jedoch nicht der Methodologie von Erfahrungswissenschaft, wie Popper sie in der Logik der Forschung vorgeschlagen hat. Danach soll Erfahrungswissenschaft neuer Erfahrung bzw. der Widerlegung von Beobachtungshypothesen systematisch dadurch Rechnung tragen, dass nach solchen Widerlegungen stets gesucht und beim Scheitern eines Experiments auch nach Konsequenzen für die jeweils beteiligte Theorie gefragt werden sollte. Das Umdefinieren von theoretischen Begriffen oder die Rettung von Beobachtungen durch Hilfshypothesen lehnt daher Popper als konventionalistische Wendung bzw. Immunisierungsstrategie ab.

Gerade der Konventionalismus lieferte indes Popper gegenüber dem logischen Positivismus (Wiener Kreis) die Begründung dafür, dass eine eigene Methodologie der empirischen Wissenschaften notwendig sei. Denn die Abgrenzung vom Konventionalismus kann nicht erkenntnislogisch, sondern nur durch methodologische Entscheidungen erfolgen (nämlich darüber, wie man im Falle von widersprechenden Beobachtungsergebnissen mit der Theorie umzuspringen habe).

Wolfgang Stegmüller hat einen Versuch vorgelegt, den Theorienwandel im Anschluss an Thomas S. Kuhn historisch zu deuten, und zwar mittels mengentheoretischer Strukturen. Damit übt er Kritik an Poppers Methodologie, sie fasse wissenschaftliche Gesetzesaussagen als All- und Existenzsätze auf und verkenne damit, dass etwa die Physik ihre Behauptungen in mathematischen Strukturen formuliere.[6] Nach der strukturalistischen Sichtweise physikalischer Theorien, wie Stegmüller sie vorschlägt, ist nicht mehr sinnvoll zu sagen, dass Teile eines Theoriekerns durch empirische Beobachtungen widerlegt werden könnten. Zum Beispiel: Noch nie hat jemand angegeben, wie empirische Daten beschaffen sein müssten, um das zweite newtonsche Gesetz zu falsifizieren.[7]

Die Kontroverse läuft somit im Grunde auf folgende Fragen hinaus: 1. inwieweit die Trennung von synthetischen und analytischen Aussagen immer strikt durchführbar sei, und 2. ob Theorien immer nur als Ganzheit geprüft werden können; dabei sei im Falle eines empirischen Misserfolgs nie bekannt, an welchem Bestandteil der Theorie oder der Prüfbedingungen der Fehler liege (Duhem-Quine-These).

Verwendung des Begriffs in anderen Wissenschaften

Der Konventionalismus in der Sprachphilosophie behauptet, logische und sprachliche Regeln seien nur semantische Konventionen. Diese Auffassung richtete sich gegen die These, dass Wörter als Abbilder eine natürliche Beziehung zum jeweils vorgestellten Objekt haben. In der neueren Linguistik entwickelte Ferdinand de Saussure den Konventionalismus weiter.

Philosophische Strömungen, die dem mathematischen Formalismus zuzurechnen sind, weisen ebenfalls konventionalistische Tendenzen auf.

Konventionalismus in der Ethik bezeichnet eine Theorie, die davon ausgeht, dass moralische Prinzipien und Urteile nicht in der Natur der Dinge oder in der menschlichen Natur begründet sind, sondern durch gesellschaftliche Konventionen und Gewohnheiten (so z. B. John Niemeyer Findlay).

Eine modernere Variante des Konventionalismus stellt der Sozialkonstruktivismus dar.

Siehe auch

Literatur

Henri Poincaré: Science et méthode. Flammarion, Paris 1908 (Bibliothèque de philosophie scientifique).
Henri Poincaré: Dernières pensées. Flammarion, Paris 1913 (Bibliothèque de philosophie scientifique).
Clark Glymour: Thinking Things Through. An Introduction to Philosophical Issues and Achievements. MIT Press, Cambridge MA u. a. 1992, ISBN 0-262-07141-X (A Bradford book).
Wesley C. Salmon: Space, Time and Motion. A Philosophical Introduction. Second Edition, revised. University of Minnesota Press, Minneapolis MN 1980, ISBN 0-8166-1044-5.
Nick Huggett (Hrsg.): Space from Zeno to Einstein. Classic Readings with a Contemporary Commentary. MIT Press, Cambridge MA u. a. 1999, ISBN 0-262-08271-3 (A Bradford book).
Karl R. Popper: Die beiden Grundprobleme der Erkenntnistheorie. Aufgrund von Mss. aus den Jahren 1930–1933 Herausgegeben von Troels Eggers Hansen. 2. verbesserte Auflage. Mohr, Tübingen 1994, ISBN 3-16-145774-9 (Die Einheit der Gesellschaftswissenschaften 18).

Einzelnachweise

Victor Kraft: Das Problem der Induktion. Zeitschrift für allgemeine Wissenschaftstheorie. 1, 1970, S. 80f.
Karl R. Popper: Logik der Forschung. 8. Auflage. J. C. B. Mohr (Paul Siebeck), Tübingen 1984, S. 48.
Henri Poincaré: Wissenschaft und Hypothese. Leipzig: Teubner 1904, S. 51.
Édouard Le Roy: Science et philosophie. 1899.
Etwas drastischer formuliert: „Man entschloss sich, an gewissen Ideen festzuhalten, komme was da wolle, und das Ergebnis war natürlich das Überleben dieser Ideen.“ (Paul Feyerabend: Wider den Methodenzwang. Skizze einer anarchistischen Erkenntnistheorie. Frankfurt 1976, S. 64)
Wolfgang Stegmüller: Eine kombinierte Analyse der Theoriendynamik. in: Gerard Radnitzky, Gunnar Andersson: Voraussetzungen und Grenzen der Wissenschaft. Tübingen 1981, S. 277 ff.
Wolfgang Stegmüller: Eine kombinierte Analyse der Theoriendynamik. in: Gerard Radnitzky, Gunnar Andersson: Voraussetzungen und Grenzen der Wissenschaft. Tübingen 1981, S. 299

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Victor Kraft: Das Problem der Induktion. Zeitschrift für allgemeine Wissenschaftstheorie. 1, 1970, S. 80f.

[2] Karl R. Popper: Logik der Forschung. 8. Auflage. J. C. B. Mohr (Paul Siebeck), Tübingen 1984, S. 48.

[3] Henri Poincaré: Wissenschaft und Hypothese. Leipzig: Teubner 1904, S. 51.

[4] Édouard Le Roy: Science et philosophie. 1899.

[5] Etwas drastischer formuliert: „Man entschloss sich, an gewissen Ideen festzuhalten, komme was da wolle, und das Ergebnis war natürlich das Überleben dieser Ideen.“ (Paul Feyerabend: Wider den Methodenzwang. Skizze einer anarchistischen Erkenntnistheorie. Frankfurt 1976, S. 64)

[6] Wolfgang Stegmüller: Eine kombinierte Analyse der Theoriendynamik. in: Gerard Radnitzky, Gunnar Andersson: Voraussetzungen und Grenzen der Wissenschaft. Tübingen 1981, S. 277 ff.

[7] Wolfgang Stegmüller: Eine kombinierte Analyse der Theoriendynamik. in: Gerard Radnitzky, Gunnar Andersson: Voraussetzungen und Grenzen der Wissenschaft. Tübingen 1981, S. 299