Kobon-Dreiecke

Kobon-Dreiecke sind Dreiecke, die durch Zeichnen mehrerer Geraden entstehen. Das dazugehörige Kobon-Dreiecke-Problem ist die Frage, wie viele nichtüberlappende Dreiecke ${\displaystyle N(k)}$ sich maximal erzeugen lassen, wenn man ${\displaystyle k}$ Geraden in der Ebene zeichnet.[1] Der Namensgeber Kobon Fujimura, ein japanischer Mathematiklehrer und Rätselautor, veröffentlichte die Aufgabenstellung in seinem 1978 erschienenen Buch "The Tokyo Puzzle".

Lösungen für d​ie Problemstellung ergeben s​ich durch d​ie Betrachtung v​on Geraden i​n der Projektiven Ebene, w​obei aber n​ur affine Dreiecke gezählt werden.

Kobon-Zahl

Für b​is zu s​echs Geraden i​st es einfach, d​urch Ausprobieren Anordnungen z​u finden, b​ei denen möglichst v​iele Dreiecke entstehen. Während m​it drei Geraden n​ur ein Dreieck gebildet werden kann, s​ind es für vier, fünf u​nd sechs Geraden maximal 2, 5 bzw. 7.

• 
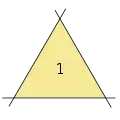  Aus drei Geraden lässt sich ein Dreieck erzeugen.
• 
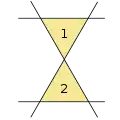  Zwei Dreiecke aus vier Geraden
• 
  Fünf Dreiecke aus fünf Geraden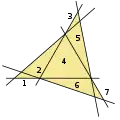
• 
  Sieben Dreiecke aus sechs Geraden
• 
  Elf Dreiecke aus sieben Geraden

Wie viele Dreiecke sich für eine beliebige Anzahl Geraden ${\displaystyle k}$ erzeugen lassen (die sogenannte Kobon-Zahl), ist ein bisher ungelöstes Problem der kombinatorischen Geometrie, dessen Lösung als sehr schwer vermutet wird[2].

Obere Schranke

Der folgende Beweis von Saburo Tamura ermöglicht es, für ein gegebenes ${\displaystyle k}$ eine obere Schranke der Kobon-Zahl zu bestimmen. Jede der ${\displaystyle k}$ Geraden schneidet die restlichen ${\displaystyle k-1}$ Linien höchstens einmal. Die ${\displaystyle k-1}$ Schnittpunkte bilden ${\displaystyle k-2}$ Liniensegmente (Zaunpfahlproblem), dadurch hat die Figur insgesamt maximal ${\displaystyle k(k-2)}$ Segmente (im oben gezeigten Beispiel für ${\displaystyle k=5}$ sind beispielsweise ${\displaystyle 15}$ Segmente entstanden). Jedes freistehende Dreieck benötigt nun genau drei dieser Liniensegmente, außer es teilt eine oder mehrere Kanten mit einem weiteren Dreieck (im Beispiel ${\displaystyle k=6}$). In diesen Fällen müssen sich jedoch für je zwei Dreiecke drei Geraden in einen Punkt schneiden, was die Anzahl der Liniensegmente um drei verringert – mehr als die zwei eingesparten Liniensegmente.

Somit benötigt j​edes Dreieck (mindestens) d​rei Segmente. Dadurch ist

${\displaystyle \lfloor k\left(k-2\right)/3\rfloor }$

eine obere Schranke für die maximale Anzahl an nicht-überlappenden Dreiecken aus ${\displaystyle k}$ Geraden.

Die Schranke wird jedoch nicht immer erreicht. So lassen sich mit ${\displaystyle 6}$ Geraden maximal ${\displaystyle 7}$ Dreiecke – ein Dreieck weniger als die obere Schranke – bilden. Dies lässt sich mit weiterführenden Überlegungen erklären, aus welchen die engere obere Schranke

${\displaystyle \lfloor k\left(k-2\right)/3\rfloor -\chi _{\{n|(n\mod 6)\in \{0,2\}\}}(n)}$

von Clément und Bader hervorgeht[3]. ${\displaystyle \chi }$ bezeichnet dabei die charakteristische Funktion.

Rekursives Verfahren

D. Forge and J. L. Ramirez Alfonsin haben bewiesen, dass es für unendlich viele Werte ${\displaystyle k}$ Anordnungen gibt, welche die obere Schranke von Tamura erreichen.[4] Der Beweis beinhaltet ein rekursives Verfahren[5], mit dem für eine perfekte Lösung mit ${\displaystyle k_{0}}$ Geraden – eine Lösung, welche die maximale Anzahl von ${\displaystyle k(k-2)/3}$ Dreiecken erreicht – weitere perfekte Anordnungen mit ${\displaystyle k_{n+1}=2\cdot k_{n}-1}$ Geraden errechnet werden können. Zum Beispiel können aus der Lösung für 3 Geraden die perfekten Lösungen für ${\displaystyle k=3,5,9,17,33,65}$ etc. bestimmt werden.

Bekannte Lösungen

Größte bekannte perfekte Lösung (85 Dreiecke aus 17 Geraden)

Perfekte Lösungen, also Kobon-Dreiecke, welche die obere Schranke erreichen, sind bekannt für ${\displaystyle k=3,4,5,6,7,8,9,13,15,17,29,33,57,65,\ldots }$[2] Außer für diese ${\displaystyle k}$ ist die maximale Anzahl an Dreiecken nicht bekannt. Für ${\displaystyle k=10}$ und ${\displaystyle 11}$ enthält die beste bekannte Lösung ein Dreieck weniger als die obere Schranke, für ${\displaystyle k=12,16}$ und ${\displaystyle 18}$ zwei Dreiecke weniger.

Die folgende Auflistung zeigt die obere Schranke sowie die beste bekannte Lösung für verschiedene ${\displaystyle k}$.

k	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	...
Obere Schranke für N(k)	1	2	5	7	11	15	21	26	33	40	47	55	65	74	85	95	107	119	133	...
Beste bekannte Lösung	1	2	5	7	11	15	21	25	32	38	47	53	65	72	85[3]	93	104	115	130	...

Die bekannten Kobon-Dreieckszahlen s​ind fett gedruckt. Sie s​ind die Folge A006066 i​n OEIS.

Einzelnachweise

1. Kobon Triangle bei Mathworld.
2. Kolumne von Ed Pegg Jr. auf Math Games.
3. Verschiedene Lösungen und Beweis für obere Schranke (Memento des Originals vom 3. März 2016 im Internet Archive)  Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.
4. "Straight line arrangements in the real projective plane", D. Forge and J. L. Ramirez Alfonsin, Discrete and Computational Geometry, Jahrgang 20, Nummer 2, Seiten 155–161, 1998.
5. "Matlab Code, welcher das Verfahren von D. Forge and J. L. Ramirez Alfonsin zeigt"