Kartenentwurfslehre
Die Kartenentwurfslehre (auch Kartennetzentwurfslehre) umfasst jene mathematischen Methoden, die zum Entwurf exakter Kartennetze und für die Berechnung geodätischer Abbildungen entwickelt wurden. Sie ist ein Teilgebiet der mathematischen Kartografie, wird aber gleichermaßen der theoretischen Geodäsie zugeordnet.
Ein Kartennetzentwurf besteht in einer eindeutigen Vorschrift, wie die gekrümmte Erdoberfläche mit ihren Breiten- und Längenkreisen auf die ebene Fläche einer Landkarte oder eines Planes abzubilden ist. Man erreicht dies
- grafisch durch eine geometrische Konstruktion
- oder rechnerisch (analytisch) durch ein System mathematischer Formeln.
Das Ergebnis ist ein Netz sich kreuzender Linien, die den Breiten- und Längenkreisen auf der Erde entsprechen. Dabei kommt es unvermeidlich zu Verzerrungen, weil sich eine zweifach gekrümmte Fläche (die Erdkugel oder das Erdellipsoid) nicht ohne Formänderungen auf eine Ebene übertragen lässt -- siehe das Einreißen einer Orangenschale, wenn man sie auf dem Teller flachdrückt.
Die ersten grafischen Kartennetzentwürfe sind aus der griechischen Antike überliefert: die quadratische Plattkarte und die stereografische Projektion. Um die Zeitenwende wurden bereits einfache rechnerische Methoden entwickelt. Wenn nun das Kartennetz vorliegt, können beliebig viele Punkte oder Linien der Erdoberfläche durch ihre geografische Breite und Länge in das Netz übertragen werden.
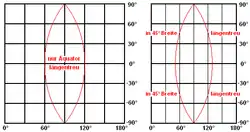
Das einfachste Kartennetz ist ein rechtwinkliger Raster von Breiten und Längen, die sog. quadratische Plattkarte. Dehnt man aber den Raster vom Äquator bis zu 90° Breite aus, so werden die Pole zu Linien, die so lang wie der Äquator sind. Zur Vermeidung solcher Verzerrungen hat Gerhard Mercator um 1600 ein ebenfalls rechtwinkliges Kartennetz erdacht, dessen Breitenkreise aber zu den Polen immer größere Abstände haben. Diese Mercator-Projektion vergrößert zwar die Flächen, gewährleistet aber ihre richtige Form (Winkeltreue).
Die streng mathematische Kartenentwurfslehre geht auf Nicolas Auguste Tissot zurück, der um 1850 die Theorie der Kartenverzerrungen entwickelte. Die Tissotsche Indikatrix gibt an, zu welcher Ellipse sich ein kleiner Kreis auf der Erdkugel verformt, wenn man ihn mit den gewählten Formeln auf die Karte projiziert. Mit Tissots Theorie lassen sich auch diejenigen Formeln ermitteln, die eine gewünschte Eigenschaft der Kartenprojektion hervorrufen. Auf diese Art wird z. B. berechnet, wie die Erde (das "Urbild") auf einen Kegel abzubilden ist, wenn eine Flugroute über den Atlantik möglichst wenig verzerrt erscheinen soll. Ähnliche Verfahren werden in der Geodäsie eingesetzt, um die Vermessungspunkte möglichst gut in digitale Koordinaten umrechnen zu können. Eine weit verbreitete Methode hierfür ist die Gauß-Krüger-Projektion. Sie ändert zwar die Entfernungen zwischen den Punkten geringfügig, lässt aber die Winkel unverändert (siehe Winkeltreue).
In der Geografie wiederum ist es wichtig, die Flächen der Länder möglichst genau wiederzugeben. Die Kartenentwurfslehre kennt eine Reihe exakt flächentreuer Projektionen, von denen man die geeignetste auswählen kann. Sie wird für ein längliches Land wie Chile anders aussehen als für ein sehr großes Land oder gar eine ganze Hemisphäre. Allerdings schließen sich Winkel- und Flächentreue gegenseitig aus, sodass man in der Geografie gewisse Formänderungen von Grenzen oder der Küsten in Kauf nehmen muss. Auch Längentreue lässt sich nur in bestimmten Richtungen erreichen, und nie gleichzeitig in Nord-Süd und Ost-West.