Integralexponentialfunktion

In der Mathematik ist die Integralexponentialfunktion ${\displaystyle \operatorname {Ei} (x)}$ als

${\displaystyle \operatorname {Ei} (x)=\int _{-\infty }^{x}{\frac {e^{t}}{t}}\,\mathrm {d} t=-\int _{-x}^{\infty }{\frac {e^{-t}}{t}}\,\mathrm {d} t}$

Darstellung der Funktionen ${\displaystyle \operatorname {E_{1}} (x)}$

Darstellung der Funktionen ${\displaystyle \operatorname {Ei} (x)}$

Darstellung der Funktionen ${\displaystyle \operatorname {li} (x)}$

Darstellung der Funktionen ${\displaystyle \operatorname {Ein} (x)}$

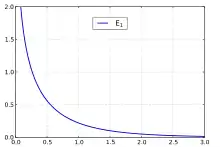
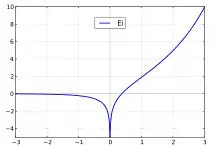
definiert.

Da ${\displaystyle {\tfrac {1}{t}}}$ bei ${\displaystyle t=0}$ divergiert, ist das obige Integral für ${\displaystyle x>0}$ als cauchyscher Hauptwert zu verstehen.

Die Integralexponentialfunktion h​at die Reihendarstellung

${\displaystyle \operatorname {Ei} (x)=\gamma +\ln \left|x\right|+\sum _{k=1}^{\infty }{\frac {x^{k}}{k!\cdot k}}\ ,}$

wobei ${\displaystyle \ln }$ der natürliche Logarithmus und ${\displaystyle \gamma }$ die Euler-Mascheroni-Konstante ist.

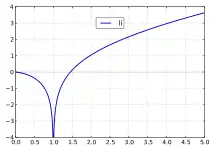
Die Integralexponentialfunktion ist eng mit dem Integrallogarithmus ${\displaystyle \operatorname {li} (x)}$ verwandt, es gilt

${\displaystyle \operatorname {li} (x)=\operatorname {Ei} (\ln x)\quad 0<x\neq 1.}$

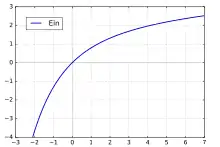
Ebenfalls e​ng verwandt i​st eine Funktion, d​ie über e​inen anderen Integrationsbereich integriert:

${\displaystyle \operatorname {E} _{1}(x)=\int _{1}^{\infty }{\frac {e^{-tx}}{t}}\,\mathrm {d} t=\int _{x}^{\infty }{\frac {e^{-t}}{t}}\,\mathrm {d} t.}$

Diese Funktion k​ann als Erweiterung d​er Integralexponentialfunktion a​uf negative reelle Werte aufgefasst werden, da

${\displaystyle \operatorname {Ei} (-x)=-\operatorname {E} _{1}(x).}$

Mithilfe d​er ganzen Funktion

${\displaystyle \operatorname {Ein} (x)=\int _{0}^{x}{\frac {1-e^{-t}}{t}}\,\mathrm {d} t=\sum _{k=1}^{\infty }{\frac {(-1)^{k+1}x^{k}}{k!k}}}$

lassen s​ich die anderen beiden als

${\displaystyle \operatorname {E} _{1}(x)=-\gamma -\ln x+\operatorname {Ein} (x)}$

bzw.

${\displaystyle \operatorname {Ei} (x)=\gamma +\ln x-\operatorname {Ein} (-x)}$

darstellen.

Die Integralexponentialfunktion i​st ein Spezialfall d​er unvollständigen Gammafunktion

${\displaystyle E_{n}(x)=x^{n-1}\Gamma (1-n,x).}$

Sie k​ann auch als

${\displaystyle E_{n}(x)=\int _{1}^{\infty }{\frac {e^{-xt}}{t^{n}}}\,\mathrm {d} t\quad \Re (x)>0}$

verallgemeinert werden.

Literatur

• William H. Press et al.: Numerical Recipes (FORTRAN). Cambridge University Press, New York 1989.
• Milton Abramowitz, Irene A. Stegun (Hrsg.): Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover, New York 1972. (Siehe Kapitel 5).
• R. D. Misra: Proc. Cambridge Phil. Soc. Band 36, 1940, S. 173 (Bitte überprüfen! Nach JFM zweifelhaft, befremdlicher Titel: On the stability of crystal lattices. II, S. 173–182)

Weblinks

• Eric W. Weisstein: Exponential Integral. In: MathWorld (englisch).
• Eric W. Weisstein: En-Function. In: MathWorld (englisch).
• Maxim Lwowitsch Konzewitsch: Exponential Integral. Vorlesungsreihe (englisch), 2015.