Dirichlet-Kern

Der Dirichlet-Kern i​st eine v​on Peter Gustav Lejeune Dirichlet untersuchte Funktionenfolge. Diese w​ird in d​er Analysis i​m Teilgebiet d​er Fourier-Analysis verwendet. Dirichlet f​and im Jahr 1829 d​en ersten strengen Beweis für d​ie Konvergenz d​er Fourier-Reihe v​on einer periodischen, stückweise stetigen u​nd stückweise monotonen Funktion. Die Konvergenz v​on Fourier-Reihen w​urde schon s​eit Leonhard Euler diskutiert. Diese v​on Dirichlet gefundene Funktionenfolge i​st wichtiger Bestandteil dieses Beweises u​nd wird d​ort als Integralkern verwendet. Deshalb n​ennt man s​ie Dirichlet-Kern.

Die ersten vier Dirichlet-Kerne. (Die Funktionen sind 2π-periodisch.)

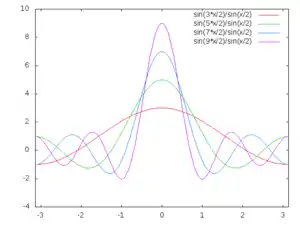
Definition

Als Dirichlet-Kern bezeichnet m​an die Funktionenfolge

${\displaystyle D_{n}(x)=\sum _{k=-n}^{n}e^{ikx}=1+2\sum _{k=1}^{n}\cos(kx)={\frac {\sin \left(\left(n+{\frac {1}{2}}\right)x\right)}{\sin(x/2)}}.}$

Die Bedeutung des Dirichlet-Kerns hängt mit dem Verhältnis zur Fourierreihe zusammen. Die Faltung von ${\displaystyle D_{n}(x)}$ mit einer Funktion ${\displaystyle f}$ der Periode ${\displaystyle 2\pi }$ ist die Fourier-Approximation ${\displaystyle n}$-ten Grades für ${\displaystyle f}$. Beispielsweise ist

${\displaystyle (D_{n}*f)(x)={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(y)D_{n}(x-y)\,dy=\sum _{k=-n}^{n}{\hat {f}}(k)e^{ikx},}$

wobei

${\displaystyle {\hat {f}}(k)={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(x)e^{-ikx}\,dx}$

der ${\displaystyle k}$-te Fourierkoeffizient von ${\displaystyle f}$ ist. Daraus lässt sich schließen, dass es zum Studium der Konvergenz von Fourierreihen ausreicht, die Eigenschaften des Dirichlet-Kerns zu studieren. Aus der Tatsache, dass die L¹-Norm von ${\displaystyle D_{n}}$ für ${\displaystyle n\to \infty }$ logarithmisch gegen ${\displaystyle \infty }$ geht, kann man herleiten, dass es stetige Funktionen gibt, die nicht durch ihre Fourierreihe dargestellt werden.[1] Explizit gilt nämlich:

${\displaystyle \int |D_{n}(t)|\,dt={\frac {4}{\pi ^{2}}}\log n+{\mathcal {O}}(1)}$

Für die ${\displaystyle {\mathcal {O}}}$-Notation siehe Landau-Symbole.

Beziehung zur Delta-Distribution

Die periodische Delta-Distribution ist das neutrale Element für die Faltung mit ${\displaystyle 2\pi }$-periodischen Funktionen:

${\displaystyle f*(2\pi \delta )=f\,}$

für jede Funktion ${\displaystyle f}$ mit Periode ${\displaystyle 2\pi }$. Die Fourierreihe wird durch folgende "Funktion" repräsentiert:

${\displaystyle 2\pi \delta (x)\sim \sum _{k=-\infty }^{\infty }e^{ikx}=\left(1+2\sum _{k=1}^{\infty }\cos(kx)\right).}$

Beweis der trigonometrischen Identität

Die trigonometrische Identität

${\displaystyle \sum _{k=-n}^{n}e^{ikx}={\frac {\sin \left(\left(n+{\frac {1}{2}}\right)x\right)}{\sin(x/2)}}}$

kann w​ie folgt bewiesen werden. Dazu vergegenwärtige m​an sich d​ie endliche Summe d​er geometrischen Reihe:

${\displaystyle \sum _{k=0}^{n}ar^{k}=a{\frac {1-r^{n+1}}{1-r}}.}$

Insbesondere gilt

${\displaystyle \sum _{k=-n}^{n}r^{k}=r^{-n}\cdot {\frac {1-r^{2n+1}}{1-r}}.}$

Multipliziert man Zähler und Nenner mit ${\displaystyle r^{-{1 \over 2}}}$, erhält man

${\displaystyle {\frac {r^{-n-1/2}}{r^{-1/2}}}\cdot {\frac {1-r^{2n+1}}{1-r}}={\frac {r^{-n-1/2}-r^{n+1/2}}{r^{-1/2}-r^{1/2}}}.}$

Im Fall von ${\displaystyle r=e^{ix}}$ erhält man

${\displaystyle \sum _{k=-n}^{n}e^{ikx}={\frac {e^{-(n+1/2)ix}-e^{(n+1/2)ix}}{e^{-ix/2}-e^{ix/2}}}={\frac {-2i\sin((n+1/2)x)}{-2i\sin(x/2)}}}$

und kürzt schließlich mit ${\displaystyle -2i}$.

Literatur

• Kurt Endl, Wolfgang Luh: Analysis II. Eine integrierte Darstellung. 7. Auflage, Aula-Verlag, Wiesbaden 1989, S. 117.
• Andrew M. Bruckner, Judith B. Bruckner, Brian S. Thomson: Real Analysis. ClassicalRealAnalysis.com 1996, ISBN 013458886X, S. 620 (vollständige Online-Version (Google Books))

Weblinks

• Dirichlet Kernel bei PlanetMath (engl.)

Einzelnachweise

1. W. Rudin, Real and Complex Analysis. McGraw-Hill, London 1970. Abschnitt 5.11, S. 101