Homokliner Orbit

Ein homokliner Orbit ist in der Mathematik dynamischer Systeme (Autonome Differentialgleichungssysteme) eine Bahnkurve (Orbit), die von einem hyperbolischen Fixpunkt (Sattelpunkt) ausgehend wieder zu diesem zurück führt. Während homokline Orbits von einem Fixpunkt zu diesem zurückführen, verlaufen heterokline Orbits zwischen zwei verschiedenen Fixpunkten, die auch Sattelpunkte sein können.

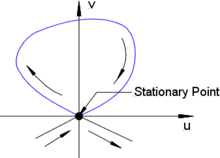
Homokliner Orbit mit hyperbolischem Fixpunkt

Bei einem hyperbolischen Fixpunkt gibt es zugehörige stabile Mannigfaltigkeiten, deren Orbits für $t\to \infty$ auf diesen zulaufen, und instabile Mannigfaltigkeiten, in denen die Punkte eines Orbits sich für $t\to -\infty$ dem Fixpunkt nähern. Die Dimension dieser Mannigfaltigkeiten richtet sich nach der Zahl positiver und negativer Realtteile von Eigenwerten bei Linearisierung der Differentialgleichung um den Fixpunkt. In zwei Dimensionen hat man eine Kurve als Orbit, die vom hyperbolischen Fixpunkt zu diesem verläuft, in mehr Dimensionen betrachtet man auch Familien von Lösungskurven und der Fixpunkt kann z. B. auch eine geschlossene Bahn sein. Mit dem Poincaré-Schnitt (dem Schnitt der Orbits mit einer Fläche senkrecht zum Phasenraumfluss) kann man das auf eine zweidimensionale Betrachtung reduzieren: der periodische Orbit (Periode $T$ ) ist im Poincaré-Schnitt ein Fixpunkt, die sich asymptotisch dem periodischen Orbit annähernden Orbits in seiner Nähe nähern sich im Poincare-Schnitt dem Fixpunkt bei der stabilen Mannigfaltigkeit bei Betrachtung des Flusses (der Iteration der Poincaré-Abbildung im Abstand $T$ ) für $t\to \infty$ und bei der instabilen Mannigfaltigkeit für $t\to -\infty$ .

Formal kann ein homokliner Orbit so definiert werden. Sei f ein Diffeomorphismus einer kompakten, nicht berandeten Mannigfaltigkeit M und p ein Fixpunkt von f ( $f(p)=p$ ). Der Orbit $f^{n}(q)$ eines Punktes $q\neq p$ ist homoklin, falls $lim_{n\to \pm \infty }f^{n}(q)=p$ . Nähert man sich für $n\to \infty$ und $n\to -\infty$ zwei verschiedenen Fixpunkten, spricht man von heteroklinem Orbit. Betrachtet man zwei Dimensionen und sei p ein hyperbolischer Fixpunkt, dann liegen die sich von p unter Iteration von f entfernenden Punkte auf einer invarianten Kurve $W^{-}(p)$ (instabile Mannigfaltigkeit) und die sich p nähernden Punkte auf $W^{+}(p)$ (stabile Mannigfaltigkeit) und homokline Punkte q liegen auf beiden Kurven ( $q\in W^{+}(p)\cap W^{-}(p)-\{p\}$ ). Der homokline Punkt q heißt transversal, falls sich $W^{\pm }(p)$ transversal in q schneiden. Mit q ist auch $f^{n}(q)$ homoklin.

Henri Poincaré fand 1888, dass das dynamische System ein sehr komplexes, chaotisches Verhalten in der Nähe des Fixpunktes zeigen kann, wenn sich auf dem homoklinen Orbit bei Störungen instabile und stabile Mannigfaltigkeit transversal schneiden (das heißt der stabile und instabile Orbit trifft sich dort nicht tangential). Zuvor hatte er angenommen, die homoklinen Orbits aus instabiler und stabiler Mannigfaltigkeit würden eine zusammenhängende Mannigfaltigkeit bilden, womit er eine Integrationsinvariante gefunden hätte und die Stabilität des vereinfachten Modells des Dreikörperproblems bewiesen hätte, das er untersuchte. Auf die Nachfrage des Gutachters der Preisarbeit, die er in Schweden eingereicht hatte, fand er aber, dass er die Möglichkeit eines transversalen Schneidens übersehen hatte. Das Bild war nun völlig anders: die instabile Mannigfaltigkeit schnitt die stabile in der Nähe des Fixpunkts unendlich oft und nahe dem Schnittpunkt führte das zu sehr chaotischem Verhalten. Entsprechendes galt auch für den anderen Ast des homoklinen Orbits, wo die stabile Mannigfaltigkeit die instabile unendlich oft schnitt. Poincaré nannte das ein homoklines Netzwerk (englisch: homoclinic tangle, in der Physik-Literatur stochastische Schichten, stochastic layers[1]) und beschrieb das über den Poincaré-Schnitt nahe dem Fixpunkt.

Der transversale Schnittpunkt der stabilen und instabilen Mannigfaltigkeit heißt transversaler homokliner Punkt (nach dem Satz von Kupka und Smale ist das der typische Fall)[2]. Da stabile und instabile Mannigfaltigkeiten des hyperbolischen Punkts invariant unter Vorwärts- und Rückwärtsiteration mit einer Poincaré-Abbildung sind, gibt es, wenn es einen homoklinen Punkt gibt, unendlich viele. In der Vorwärts- und Rückwärtsiteration liegt man sowohl auf der stabilen als auch auf der instabilen Mannigfaltigkeit und das unendlich oft. Andererseits kann die instabile Mannigfaltigkeit sich nicht selbst schneiden (und analog die stabile) wegen der Eindeutigkeit der Lösung der Differentialgleichung bei gegebener Anfangsbedingung, was eine sehr komplexe Dynamik ergibt.

Das komplexe Verhalten des Systems im homoklinen Netzwerk nach Poincaré wird auch als Folge des $\lambda$ -Lemmas von Jacob Palis[3] deutlich: Seien $W^{+}(p)$ die stabile und $W^{-}(p)$ die instabile Mannigfaltigkeit zum hyperbolischen Fixpunkt p (wobei die Dimension von $W^{-}(p)$ u sei) und sei D eine u-dimensionale Scheibe transversal zu $W^{+}(p)$ . Dann konvergieren die Iterierten $f^{n}(D)$ gegen $W^{-}(p)$ . Betrachtet man zwei Dimensionen, so wird danach ein Umgebungsintervall D des transversalen homoklinen Punktes q, das auf der instabilen Mannigfaltigkeit liegt, durch Iteration schließlich in einer beliebig kleinen Umgebung eines Intervalls der instabilen Mannigfaltigkeit um den Fixpunkt p liegen.

Stephen Smale fand Anfang der 1960er Jahre eine einfache geometrische Struktur, die Hufeisen-Abbildung, die das chaotische Verhalten im homoklinen Netz erklärt. Das ist Gegenstand des Satzes von Birkhoff und Smale, der besagt, dass solch ein Hufeisen in einer beliebigen Umgebung eines hyperbolischen Fixpunkts p eines Diffeomorphismus f besteht für eine Iteration von f, falls ein transversaler homokliner Punkt q existiert.[4] Bei der Hufeisenabbildung wird ein Quadrat auf sich abgebildet, indem es gedehnt und wie ein Hufeisen zurückgebogen wird (anschaulich entspricht das der abwechselnden Expansion und Stauchung bei abwechselnder Bewegung auf der stabilen und instabilen Mannigfaltigkeit).

Birkhoff bestätigte um 1935[5] die Vermutungen von Poincaré, indem er zeigte (in zwei Dimensionen), dass es nahe homoklinen Orbits ein sehr komplexes Netz periodischer Punkte: in einer beliebig kleinen Umgebung eines transversalen homoklinen Punkt gibt es periodische Punkte[6]. In den 1940er Jahren untersuchten Mary Cartwright und John Edensor Littlewood (und in den USA Norman Levinson, dessen Arbeit die Inspiration für die Arbeit von Smale zum Hufeisen war) homokline Orbits bei der Van der Pol Gleichung, die erzwungene Schwingungen in Vakuumröhren beschreibt. Typisch war beim van der Pol Oszillator das Auftreten eines periodischen Orbits mit viel höherer Frequenz als die der Anregungsfrequenz und einem abwechselnd stabilen periodischen (mit einer Frequenz) und bistabilen chaotischen Verhalten (mit zwei Frequenzen) je nach der Größe der Anregungsamplitude (genauer durch Mark Levi 1981[7] erklärt).

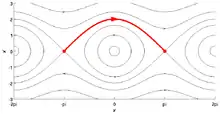
Heterokliner Orbit im Phasenraum eines Pendels

Der Begriff homokliner und heterokliner Punkt wurde von Poincaré im dritten Band seiner Méthodes Nouvelles de la Mécanique Celeste (1899, Kapitel 33) eingeführt (ursprünglich nannte er sie doppelt asymptotische Lösungen).

Literatur

Boris Hasselblatt, Anatole Katok: First course in dynamics. Cambridge University Press, 2003.
Boris Hasselblatt, Anatole Katok: Introduction to the modern theory of dynamical systems. Cambridge University Press, 1995.
Jacob Palis, Floris Takens: Hyperbolicity and Sensitive Chaotic Dynamics at Homoclinic Bifurcations. Cambridge University Press, 1993.
Jürgen Moser: Stable and random motions in dynamical systems. Princeton University Press, 1973.

Weblinks

Quiudong Wang, On the homoclinic tangles of Henri Poincaré (PDF; 4,1 MB)

Einzelnachweise

Guckenheimer, Holmes, Nonlinear oscillations, S. 222
Hasselblatt, Katok, Introduction to the modern theory of dynamical systems, S. 292
Palis, de Melo, Geometric theory of dynamical systems, Springer 1982
Hasselblatt, Katok, First Course in Dynamics, S. 322
Birkhoff, Novelles recherches sur les systèmes dynamiques, Mem. Pontific. Acad. Sci. Novi Lyncaei, 1, 1935, S. 85–216
So wird der Satz von Smale und Birkhoff auch formuliert, z. B. Mrowka, A short proof of the Birkhoff-Smale theorem, Proc. AMS, Band 93, 1985, S. 377. Er folgt als Korollar aus dem Satz von Smale und Birkhoff über die Existenz von Hufeisen, Smale, Differentiable Dynamical Systems, Bull. AMS, Band 73, 1967, S. 775, Online, und war die Formulierung, in der Birkhoff den Satz in zwei Dimensionen bewies.
Levi, Qualitative analysis of the periodically forced relaxation oscillations, Memoirs AMS 1981

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Guckenheimer, Holmes, Nonlinear oscillations, S. 222

[2] Hasselblatt, Katok, Introduction to the modern theory of dynamical systems, S. 292

[3] Palis, de Melo, Geometric theory of dynamical systems, Springer 1982

[4] Hasselblatt, Katok, First Course in Dynamics, S. 322

[5] Birkhoff, Novelles recherches sur les systèmes dynamiques, Mem. Pontific. Acad. Sci. Novi Lyncaei, 1, 1935, S. 85–216

[6] So wird der Satz von Smale und Birkhoff auch formuliert, z. B. Mrowka, A short proof of the Birkhoff-Smale theorem, Proc. AMS, Band 93, 1985, S. 377. Er folgt als Korollar aus dem Satz von Smale und Birkhoff über die Existenz von Hufeisen, Smale, Differentiable Dynamical Systems, Bull. AMS, Band 73, 1967, S. 775, Online, und war die Formulierung, in der Birkhoff den Satz in zwei Dimensionen bewies.

[7] Levi, Qualitative analysis of the periodically forced relaxation oscillations, Memoirs AMS 1981