Hermitesche Funktion

Die Hermiteschen Funktionen $h_{n}(x)$ erhält man aus den Hermiteschen Polynomen $H_{n}(x)$ , indem man diese mit der Dichte der Gaußschen Normalverteilung multipliziert.

h_{n}(x)={\frac {(-1)^{n}}{\sqrt {2^{n}n!{\sqrt {\pi }}}}}e^{x^{2}/2}{\frac {\mathrm {d} ^{n}}{\mathrm {d} x^{n}}}e^{-x^{2}}={\frac {1}{\sqrt {2^{n}n!{\sqrt {\pi }}}}}H_{n}(x)e^{-{\frac {1}{2}}x^{2}},

\int _{-\infty }^{\infty }h_{n}(x)h_{m}(x)\,\mathrm {d} x=\delta _{n,m}\qquad \qquad n,m=0,1,2,\ldots

Plot der ersten fünf Hermiteschen Funktionen h_n bzw. ψ_n

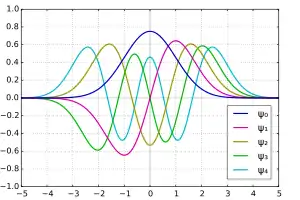
Sie sind ein sehr gutes Beispiel für die Definition (Erzeugung) einer orthonormalen Basis, ähnlich der Sinus-/Kosinusfunktionen. Während letztere in der Lage sind, mittels der Spektralanalyse (Fourieranalyse) ein periodisches Signal in ein Frequenzspektrum zu zerlegen, erlauben die Hermiteschen Funktionen die Beschreibung singulärer Ereignisse.

Eine wichtige Bedeutung haben sie in der Physik zur Konstruktion der orthonormierten Lösungsfunktionen des quantenmechanischen harmonischen Oszillators. Motiviert durch die Erzeugungs- und Vernichtungsoperatoren der Quantenmechanik erhält man folgende rekursive Darstellung der hermiteschen Funktionen

h_{n}(x)=n^{-{\frac {1}{2}}}a^{\dagger }h_{n-1}(x),\qquad h_{0}(x)=\pi ^{-{\frac {1}{4}}}e^{-{\frac {1}{2}}x^{2}},

dabei ist der Operator $a^{\dagger }$ definiert durch

a^{\dagger }={\frac {1}{\sqrt {2}}}{\Big (}x-{\frac {\mathrm {d} }{\mathrm {d} x}}{\Big )}.

Singuläre Ereignisse werden in der Regel durch Intensität, Mittelwert und Standardabweichung charakterisiert. Diese Kennwerte können aber für verschiedene, sehr unterschiedliche Ereignisse identisch sein, so dass sie für die Charakterisierung nicht ausreichen. Daher bestimmt man die sogenannten „höheren statistischen Momente“ als weitere Vergleichsgrößen. Diese sind jedoch sehr empfindlich auf Rauschen und Drift der Nulllinie und daher nur bedingt geeignet. Entwickelt man eine Verteilung in Hermiteschen Funktionen, so sind die Koeffizienten sehr stabil, da die Funktionen nur im zentralen Bereich leben und somit weiter außenliegende Messdaten geeignet dämpfen.

Die Entwicklung einer ein Ereignis repräsentierenden Funktion nach Hermiteschen Funktionen hat eine gewisse Ähnlichkeit mit der Wavelet-Transformation.

Hermitesche Funktionen als Eigenfunktionen der Fourier-Transformation

Die Hermiteschen Funktionen sind Eigenfunktionen der Fourier-Transformation im Eindimensionalen zu den Eigenwerten $\left(-\mathrm {i} \right)^{n}$ :

{\mathcal {F}}\,h_{n}=\left(-\mathrm {i} \right)^{n}\,h_{n}\qquad \left(n\in \mathbb {N} _{0}\right).

Mehr noch, sie bilden ferner im Raum $L^{2}\left(\mathbb {R} \right)$ ein vollständiges Orthonormalsystem von Eigenfunktionen.[1]

Literatur

I. N. Bronstein, K. A. Semendjajew (Begründer), Günter Grosche (Bearb.), Eberhard Zeidler (Hrsg.): Teubner-Taschenbuch der Mathematik. Teubner, Stuttgart 1996, ISBN 3-8154-2001-6.

Einzelnachweise

Helmut Fischer, Helmut Kaul: Mathematik für Physiker, Band 2: Gewöhnliche und partielle Differentialgleichungen, mathematische Grundlagen der Quantenmechanik. 2. Aufl., B.G. Teubner, Wiesbaden 2004. ISBN 3-519-12080-1, §12 Abschn. 4.2, S. 300–301.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Helmut Fischer, Helmut Kaul: Mathematik für Physiker, Band 2: Gewöhnliche und partielle Differentialgleichungen, mathematische Grundlagen der Quantenmechanik. 2. Aufl., B.G. Teubner, Wiesbaden 2004. ISBN 3-519-12080-1, §12 Abschn. 4.2, S. 300–301.