Teilerbild
Das Teilerbild (auch Teilerdiagramm) ist ein Diagramm, in dem alle Teiler einer Zahl nach einem bestimmten Schema dargestellt sind. Für dieses Schema spielen die Primfaktoren eine besondere Rolle. Das Teilerbild ist eine spezielle Variante des Hasse-Diagramms.
Aufbau eines Teilerbilds
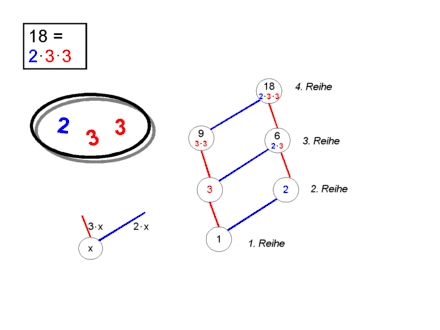
siehe Bild mit dem Beispiel 18.
- In der untersten Reihe steht immer die 1.
- In der 2. Reihe stehen die Primfaktoren der Zahl.
- Im Beispiel die 2 und die 3.
- In der 3. Reihe die Teiler der Zahl, die aus 2 Primfaktoren zusammengesetzt sind.
- im Beispiel die 6 (= 2 · 3) und die 9 (= 3 · 3).
- Es folgen die Reihen mit 3, 4 usw. Primfaktoren,
- in der obersten Reihe steht die Zahl, um die es geht (hier 18).
Jeder Teiler im Bild ist mit seinen Teilern und Vielfachen in den benachbarten Reihen verbunden. Im Bild symbolisieren
- die blauen Linien eine Multiplikation mit 2,
- die roten Linien eine Multiplikation mit 3.
So werden auf dem Weg von der 1 zur 18 immer zwei rote Linien und eine blaue Linie benutzt, was der Rechnung 2 · 3 · 3 = 18 entspricht, bzw. 3 · 3 · 2 oder 3 · 2 · 3.
Erstellen des Teilerbilds mithilfe der Primfaktoren
(siehe Beispielbild: Zahl 18)
- Durch Primfaktorzerlegung bestimmt man die Primfaktoren der gefragten Zahl.
- In die unterste Reihe schreibt man die 1, in die 2. Reihe die Primfaktoren, im Beispiel die 2 und die 3.
- Die Primfaktoren werden mit der 1 durch Linien verbunden. Die Linie von der 1 zur 2 (blaue Linie im Beispiel) bedeutet nun „nimm mal 2“, die Linie von der 1 zur 3 (rot) „nimm mal 3“ usw.
- Von der 2. Reihe kommt man in die 3. Reihe, indem man an die Teiler weitere Linien anfügt. So ergibt sich aus der 3 mit einer blauen Linie die 6 („nimm mal 2“) und mit einer Roten Linie die 9 („nimm mal 3“). Aus der 2 ergibt sich mit einer roten Linie auch die 6. An die 2 darf keine weitere blaue Linie angefügt werden, da die 2 in der Primfaktorzerlegung von 18 nur einmal vorkommt.
Nun gelangt man von der 1 über 2 rote Linien (3 · 3) zur 9, sowie über rot, blau (3 · 2) zur 6 und über blau, rot (2 · 3)auch zur 6.
- Zur 4. Reihe geht es entsprechend weiter. an die 9 darf nur noch die blaue Linie anschließen, da beide 3en auf dem Weg von der 1 zur 9 schon verbraucht wurden und nurmehr die 2 übrig ist. Dies führt zur 18 (9 · 2). An der 6 darf nur die rote Linie folgen, da die einzige verfügbare 2 auf dem Weg zur 6 schon verbraucht wurde. Auch 6 · 3 ergibt 18.
Erstellen des Teilerbilds – spielerische Methode
- Durch Primfaktorzerlegung bestimmt man die Primfaktoren der gefragten Zahl.
- Man schreibt jeden Primfaktor auf ein Kärtchen und gibt alle Kärtchen in eine Lostrommel (Tasse o. ä.).
- Bei der 18 bekommt man 3 Kärtchen, eins mit 2 beschriftet und zwei mit 3 beschriftet.
- Das Teilerbild wird in der untersten Reihe mit der 1 begonnen.
- Die 2. Reihe: Man schreibt alle Zahlen auf, die überhaupt auf den Kärtchen abgebildet sind.
- Bei der 18 sind dies 2 und 3. Die 3 wird nur einmal in das Teilerbild geschrieben, auch wenn sie zweimal in der 18 vorkommt (2 · 3 · 3).
- Die 3. Reihe: Man zieht blind zwei Kärtchen, nimmt die Zahlen miteinander mal und schreibt das Ergebnis in die 3. Reihe. Dieses wiederholt man ein paar Mal, bis man alle Teiler der 3. Reihe zusammen hat.
- So bekommt man die 9 (3 · 3) und die 6 (3 · 2). Die 4 (2 · 2) bekommt man nicht, da die 2 nur einmal im Topf ist. Sie ist auch kein Teiler von 18.
- Die 4. Reihe: Hier zieht man 3 Kärtchen und multipliziert sie und schreibt die Ergebnisse auf.
- Im Beispiel bekommt man so die 18. Dies sind alle Kärtchen im Topf und das Spiel ist zu Ende.
- anschließend verbindet man noch alle Zahlen, die in Teiler oder Vielfache voneinander sind, wenn sie in benachbarten Reihen stehen.
Weiteres
Strukturiertes Teilerbild und Rechenschablone
Beim Erstellen des Teilerbilds empfiehlt es sich, alle Linien, die eine bestimmte Operation anzeigen (z. B. alle "x2"-Linien) in derselben Richtung und Länge auszuführen. So ergibt sich ein strukturiertes Bild. Außerdem kann man sich nun eine Rechenschablone erstellen, wie in den Beispielbildern angedeutet. Legt man das "X" auf eine Zahl im Teilerbild, bekommt man am Ende der Linien das passende Ergebnis.
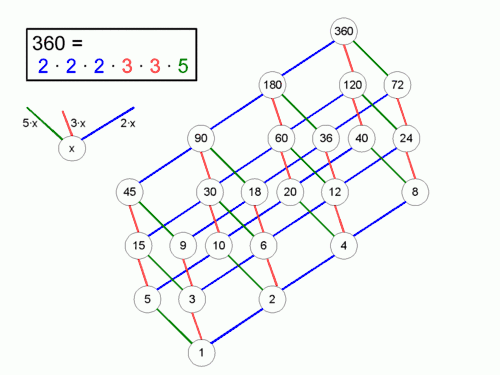
Teil-Teilerbilder
Hat man bereits das Bild einer großen Zahl angefertigt und benötigt dann das Bild einer Zahl, die Teiler der ersten Zahl ist, so kann man das Teilerdiagramm der großen Zahl verwenden, indem man einige Zahlen streicht.
Beispiel: Man hat schon das Teilerbild der 360. Wird nun das Bild der 180 gebraucht, entfernt man die Zahlen 360, 120, 40, 72, 24 und 8 aus dem 360er Bild und schon ist es fertig.
Teilerbilder verlängern
Umgekehrt lässt sich auch aus einem Bild einer kleinen Zahl das einer großen Zahl machen, indem man "etwas dranhängt". Dazu muss die große Zahl ein Vielfaches der kleinen Zahl sein.
Beispiel: Für ein Bild der 720 nimmt man wieder das 360er Bild und verlängert es über die 8 hinaus mit einer blauen Linie: 8 · 2=16. Desgleichen geschieht bei 360, 120, 40, 72 und 24.
3D-Teilerbilder
Teilerbilder mit mehr als 2 verschiedenen Primfaktoren werden schnell unübersichtlich, da sich viele Linien kreuzen. Dies kann man umgehen, indem man ein räumliches Modell baut (z. B. aus Kugeln und Stäbchen). Mit etwas Phantasie lässt sich die quaderartige Struktur des 360er Bilds in der Beispieldarstellung erkennen.