Gegendiagonale

In der Mathematik besteht die Gegendiagonale oder Antidiagonale einer quadratischen Matrix aus den Matrixelementen, die auf einer gedachten diagonal von rechts oben nach links unten verlaufenden Linie liegen. Allgemeiner bestehen die Gegendiagonalen einer Matrix aus den Matrixelementen, die auf einer beliebigen diagonalen Linie von rechts oben nach links unten liegen. Gelegentlich werden die Gegendiagonalen einer Matrix auch als „Nebendiagonalen“ bezeichnet; unter den Nebendiagonalen einer Matrix werden jedoch meist die Diagonalen der Matrix verstanden, die parallel zur Hauptdiagonale verlaufen.

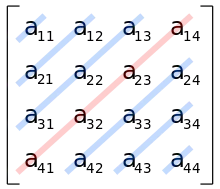
Gegendiagonale (rot) und weitere Gegendiagonalen (blau) einer (4×4)-Matrix

Die Gegendiagonalen einer Matrix werden beispielsweise in der Regel von Sarrus eingesetzt.

Definition

Die Gegendiagonale einer quadratischen Matrix

A={\begin{pmatrix}a_{1,1}&a_{1,2}&\ldots &a_{1,n}\\a_{2,1}&a_{2,2}&\ldots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\ldots &a_{n,n}\end{pmatrix}}

besteht aus denjenigen Einträgen der Matrix, die auf der Diagonale von rechts oben nach links unten liegen, also den Elementen

a_{1,n},a_{2,n-1},\ldots ,a_{n-1,2},a_{n,1}

.

Die Gegendiagonale besteht damit aus denjenigen Matrixeinträgen $a_{i,j}$ , deren Summe aus Zeilen- und Spaltenindex den Wert $n+1$ ergibt.[1] Allgemein bestehen die Gegendiagonalen einer Matrix beliebiger Größe aus denjenigen Einträgen, deren Summe aus Zeilen- und Spaltenindex konstant ist, für die also

i+j=k

mit einem konstanten Wert $k$ gilt.

Beispiel

Die Gegendiagonale der reellen Matrix

A={\begin{pmatrix}0&1&2&3\\1&2&3&4\\2&3&4&5\\3&4&5&6\end{pmatrix}}

besteht aus den Elementen $3,3,3,3$ . Die weiteren Gegendiagonalen der Matrix besitzen ebenfalls jeweils konstante Einträge. Matrizen mit dieser Eigenschaft werden Hankel-Matrizen genannt.

Verwendung

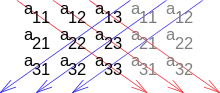
Diagonalen und Gegendiagonalen bei der Regel von Sarrus

Die Gegendiagonale einer Matrix ist das Gegenstück zur Diagonale der Matrix, welche auch als Hauptdiagonale bezeichnet wird. Die Gegendiagonalen einer Matrix sind dann die Gegenstücke zu den Diagonalen der Matrix, die außerhalb der Hauptdiagonalen auch als Nebendiagonalen der Matrix bezeichnet werden.

Bei der Regel von Sarrus wird die Determinante einer $3\times 3$ -Matrix mit Hilfe der Diagonalen und Gegendiagonalen der um die ersten beiden Spalten erweiterten Matrix berechnet.

Eine Matrix, die symmetrisch bezüglich ihrer Gegendiagonale ist, heißt persymmetrische Matrix. Eine Toeplitz-Matrix ist eine persymmetrische Matrix, bei der die Einträge auf der Hauptdiagonale und den Nebendiagonalen jeweils konstant sind. Eine Matrix, die sowohl bezüglich ihrer Diagonale, als auch bezüglich ihrer Gegendiagonale symmetrisch ist, wird bisymmetrische Matrix genannt.

Literatur

Roger A. Horn, Charles R. Johnson: Matrix Analysis. Cambridge University Press, 2012, ISBN 978-0-521-83940-2.

Einzelnachweise

Roger A. Horn, Charles Johnson: Matrix analysis. Cambridge University Press, 2013, S. 33.

Weblinks

Eric W. Weisstein: Skew diagonal. In: MathWorld (englisch).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[horn-1] Roger A. Horn, Charles Johnson: Matrix analysis. Cambridge University Press, 2013, S. 33.