Gassorptionsmessung
Eine Gassorptionsmessung[1] erlaubt die Charakterisierung der Porosität von Pulvern[2] und Festkörpern durch die Bestimmung des absorbierten Gasvolumens in Abhängigkeit vom Partialdruck. Hierbei können Mikroporen, die innere Oberfläche und Mesoporen vermessen werden.
Messverfahren und Auswertungsbereiche
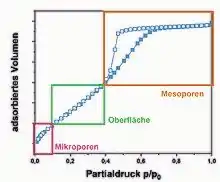
Für Gassorptionsmessungen an festen Proben wird als Messgas in der Regel Stickstoff verwendet, wobei das adsorbierte Volumen als Funktion des Partialdrucks aufgetragen wird. Vor der Analyse muss das Probenmaterial bei erhöhten Temperaturen im Vakuum behandelt werden, um bereits adsorbierte Gase oder Feuchtigkeit zu entfernen. Dies kann die Untersuchung thermisch empfindlicher Materialien erschweren.
N2-Sorptionsmessungen finden bei −196 °C statt. Bei dieser Temperatur wird davon ausgegangen, dass Physisorption durch Van-der-Waals-Wechselwirkungen mit Adsorptionsenthalpien unter 4 kJ/mol stattfindet. Wenn hierbei Adsorption und Desorption nicht identisch verlaufen, spricht man von einer Hysterese. Aus verschiedenen Bereichen der Isothermen lassen sich Informationen über Mikroporen, die innere Oberfläche und Mesoporen erhalten.[3]
Mikroporen
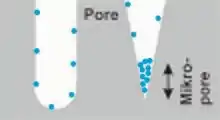
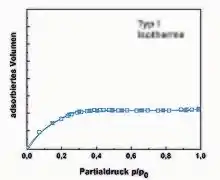
Bei nicht-porösen Materialien kann man vereinfacht von der Gasadsorption auf einer planaren Oberfläche ausgehen. Bei Mikroporen < 2 nm muss berücksichtigt werden, dass das Adsorbat auch mit einer gekrümmten Oberfläche bzw. mit einer gegenüberliegenden Porenwand wechselwirkt. Dies erhöht die effektive Adsorptionsenthalpie und führt im Gegensatz zu einem planaren Substrat zu erhöhter Adsorption bei kleineren Partialdrücken. Primär mikroporöse Feststoffe resultieren nach einer Klassifikation von Brunauer, Deming, Deming und Teller (BDDT)[4] in sogenannten Typ I-Isothermen, die keine Hysterese zeigen. Grundlegende Arbeiten zur Adsorption in mikroporösen Materialien wurden vom russischen Chemiker Michail Michailowitsch Dubinin geleistet.[5]
Innere Oberfläche
Aus dem vorderen Bereich der Sorptionsisothermen können Informationen über die spezifische Oberfläche des untersuchten Materials erhalten werden, die in m2 pro Gramm angegeben wird. Einer Auswertung der Messungen müssen Modellannahmen über den Adsorptionsvorgang zugrunde gelegt werden. So geht beispielsweise das Langmuir Modell von der Adsorption einer Monolage aus, wobei keine Wechselwirkung zwischen benachbarten Adsorbatmolekülen angenommen wird. Das Modell nach Brunauer, Emmett und Teller (BET)[6] geht von einer realistischeren Adsorption von Multilagen aus. Wenn eine Messung nach Langmuir ausgewertet wird, ist die errechnete spezifische Oberfläche immer höher als die eine BET Analyse. Ursache hierfür ist, dass alle real in den Multilagen adsorbierten Gasmoleküle nach Langmuir der spezifischen Oberfläche zugeschrieben werden, die somit überschätzt wird.
Mesoporen
Bei höheren Partialdrücken adsorbiert das Messgas in Poren mit Radien über 2 nm, wobei kleinere Poren früher gefüllt werden als größeren. Der Zusammenhang zwischen dem Gleichgewichtsdampfdruck über Flüssigkeitsmenisken und deren Krümmungsradius beschreibt hierbei die Kelvin-Gleichung. Die reale Porengeometrie wird bei den Gassorptionsmessungen durch die Gefügestruktur des jeweilig untersuchten Materials bestimmt.

Unter der Annahme einer zylindrischer Geometrie wurde 1951 von Barrett, Joyner und Halenda (BJH)[7] eine Methode veröffentlicht, um aus Sorptionsisothermen Porenradienverteilungen zu errechnen. Im Radienbereich von 2 nm bis 100 nm kann zunächst das kumulative Porenvolumen in cm3/g aufgetragen werden. Aus der Grafik ist zu entnehmen, welches Porenvolumen in einem bestimmten Radienintervall lokalisiert ist. Es ist jedoch nicht möglich, aus diesen Angaben die Gesamtporosität eines Materials bekannter Dichte zu berechnen, weil Mikroporenvolumina und das Volumen in Makroporen > 100 nm nicht erfasst werden.
Anschaulicher als die Auftragung des kumulativen Porenvolumens ist die ihrer Ableitung, die differentiellen Porenradienverteilung. Maxima bezeichnen hier den häufigsten mittleren Porenradius. In der Materialwissenschaft sind besonders Vergleiche zwischen bei verschiedenen Temperaturen behandelten Proben instruktiv, weil sich z. B. das Zusammensintern kleiner Poren und der Verlust von Mesoporosität dokumentieren lässt.

Bei der Untersuchung von mesoporösen Proben wird eine Hysterese zwischen den Adsorptions- und Desorptionsisothermen beobachtet. Dementsprechend erhält man auch unterschiedliche BJH Porenradienverteilungen, je nachdem welche Isotherme zur Auswertung herangezogen wird. Als mikroskopische Ursache der Hysterese werden in zylindrischen Poren die verschiedenen Menisken des flüssigen Adsorbates bei Adsorption und Desorption diskutiert: Beim Adsorptionsvorgang wird Innenseite des Porenzylinders mit einer wachsenden Schicht des flüssigen Messgases bedeckt, bis sie vollständig gefüllt ist. Bei der Desorption entsteht am Poreneingang ein konkaver Meniskus. In dieser gekrümmten Oberfläche sind die Wechselwirkungen zwischen den Molekülen des Adsorbats höher als in einer planaren Adsorbatschicht, weshalb die Desorption bei niedrigeren Partialdrücken stattfindet. Unter Zuhilfenahme der Kelvin-Gleichung kann plausibel erklärt werden, dass die aus den Adsorptionsdaten abgeleitete Porenradiusverteilung doppelt so groß ist wie die aus dem Desorptionszweig.[8]
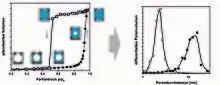
Die aus der Adsorptionsisotherme abgeleitete Porenradienverteilung kann jedoch auch deutlich mehr als das Doppelte des aus dem Desorptionszweig berechneten Wertes betragen. Dies kann durch das Vorliegen sogenannter Flaschenhalsporen, bei denen der Zugang zu einem größeren Volumen durch engere Zugänge begrenzt ist, erklärt werden. Zu Beginn findet eine Adsorption auf der gesamten inneren Oberfläche des porösen Gefüges statt. Bei erhöhten Partialdrücken können die begrenzenden Hälse gefüllt werden, aber die großen ungefüllten Hohlräume sind immer noch im Gleichgewicht mit der äußeren Umgebung. Man kann sich die Situation so vorstellen, dass die innere Blase durch adsorptive Permeation durch den Meniskus im Engpass im Gleichgewicht mit der äußeren Umgebung steht. Bei p/p0= 1 wird die Pore vollständig gefüllt. Wird der Druck nun wieder verringert, ist theoretisch zuerst die Desorptionsbedingung für die großen Poren erfüllt. Da es keinen freien Zugang zu den größeren Hohlräumen gibt, wird deren Inhalt metastabil. Erst wenn die Desorptionsbedingung des Flaschenhalses erfüllt ist, wird die große, "übersättigte" Pore schnell entleert. Dieser Argumentation folgend kann der aus den Desorptionsdaten berechnete Porenradius als Maß für die kleinen Poren genommen werden, die zu den größeren Hohlräumen Zugang haben. Der Gesamtbereich der Poren wird dann besser durch den Adsorptionszweig charakterisiert.
Siehe auch
Weblinks
- SciFox Lernvideo Auswertung von Adsorptionsisothermen
Einzelnachweise
- .S. J Gregg, K. S. W Sing: Adsorption, surface area, and porosity,. Academic Press, London/New York 1967.
- S. Lowell, Joan E. Shields: Powder Surface Area and Porosity. 3. Auflage. Springer Netherlands, Dordrecht 2013, ISBN 978-94-015-7955-1.
- Raoof Bardestani, Gregory S. Patience, Serge Kaliaguine: Experimental methods in chemical engineering: specific surface area and pore size distribution measurements—BET, BJH, and DFT. In: The Canadian Journal of Chemical Engineering. Band 97, Nr. 11, 2019, S. 2781–2791, doi:10.1002/cjce.23632.
- Brunauer, S., Deming, L.S., Deming, W.E. and Teller, E. (1940) On a Theory of the van der Waals Adsorption of Gases. Journal of the American Chemical Society, 62, 1723–1732. https://doi.org/10.1021/ja01864a025
- M. M. Dubinin: The Potential Theory of Adsorption of Gases and Vapors for Adsorbents with Energetically Nonuniform Surfaces. In: Chemical Reviews. Band 60, Nr. 2, 1960, S. 235–241, doi:10.1021/cr60204a006.
- Naderi, Majid. "Surface Area: Brunauer–Emmett–Teller (BET)." Progress in filtration and separation. Academic Press, 2015. 585–608.
- Barrett, Elliott P., Leslie G. Joyner, and Paul P. Halenda. "The determination of pore volume and area distributions in porous substances. I. Computations from nitrogen isotherms." Journal of the American Chemical society 73.1 (1951): 373–380.
- Peer Löbmann “Characterization of sol–gel thin films by ellipsometric porosimetry”, J Sol-Gel Sci.Tec. 84 (2017) 2–15, DOI 10.1007/s10971-017-4473-1.