Fehlerkorrekturmodell

Das Fehlerkorrekturmodell (kurz: FKM) ist ein statistisches Modell aus dem Bereich der Ökonometrie und Zeitreihenanalyse. Es wurde von Clive Granger entwickelt, der dafür 2003 mit dem Alfred-Nobel-Gedächtnispreis für Wirtschaftswissenschaften ausgezeichnet wurde. Mit einem Fehlerkorrekturmodell wird die kurzfristige Dynamik eines sonst langfristig gleichgewichtigen Systems ausgewiesen, um so die Möglichkeit zu eröffnen, diese getrennt voneinander zu betrachten. Im Englischen wird es als Error Correction Model oder kurz ECM bezeichnet, diese Abkürzung ist auch im deutschen Sprachraum üblich. Ein Vektor-Fehlerkorrekturmodell (kurz: VECM, für Vector Error Correction Model) ist vor allem geeignet, wenn ein System aus Zeitreihen zwar nicht stationär in den Niveaus, aber stationär in den Differenzen ist. Würde die Langfristdynamik ohne Vektor-Fehlerkorrekturmodell getestet, würde starke Autokorrelation zwischen den Residuen auftreten, da sie die Kurzfristdynamik enthalten würden.

Anwendung

Mögliche Kointegration von zwei Variablen und damit Anwendung des Fehlerkorrekturmodelles

Voraussetzung für eine sinnvolle Anwendung des Fehlerkorrekturmodelles sind:

Es sind 2 oder mehr Variablen (Merkmale) vorhanden.
Diese Variablen müssen eine zeitliche Reihenfolge besitzen, sie stellen damit Zeitreihen dar. Ein Beispiel ist die Entwicklung eines Aktienkurses über eine gewisse Zeitspanne.
Die Variablen stehen in einem sinnvollen Zusammenhang zueinander. Der Zusammenhang sollte möglichst auch inhaltlich begründbar sein. Ein Beispiel ist ein Zusammenhang zwischen der Entwicklung der Bruttosozialprodukte zweier Länder. Falls diese Länder wirtschaftlich verbunden sind, können sich die BSP mit einer gemeinsamen Tendenz (Trend) entwickeln. Eine Krise in dem einen Land führt ebenfalls zu einer Krise im anderen Land, ebenso für wirtschaftliche Aufschwünge.
Die Variablen (Zeitreihen) sind dann zueinander kointegriert. Dies bedeutet zunächst, dass jede Zeitreihe für sich nichtstationär ist. Nichtstationarität bedeutet in der Praxis, dass die Zeitreihen meist einen Trend haben. Zusätzlich können ungleichmäßige Schwankungen (Heteroskedastizität) oder streng periodische Schwankungen auf Nichtstationarität hinweisen. In der Praxis haben die Zeitreihen meist einen ungefähren Gleichlauf über die Zeit, damit sind sie gemeinsam integriert, also kointegriert. Der Begriff Integration bedeutet, dass die nichtstationären Zeitreihen durch Differenzenbildung auf neue stationäre Zeitreihen zurückgeführt werden können.

Vorgehensweise

Es ist zu beachten, dass bei numerisch bekannten Kointegrationsvektor sich die Gleichgewichtsabweichungen, die eine Fehlerkorrektur auslösen, aus den Beobachtungen der einzelnen Zeitreihen berechnen lassen. Dieser ist aber meist (immer) unbekannt, daher ersetzt man die Abweichungen zum Gleichgewicht durch Proxywerte, um mithilfe einer einfachen KQ-Regression die Koeffizienten des Fehlerkorrekturmodells approximativ schätzen zu können. Nachfolgend werden die dafür notwendigen Schritte erklärt:

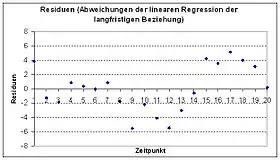
Residuen der langfristigen Beziehung

Es ist zuerst die langfristige Beziehung der Variablen zu schätzen. Dazu wird ein einfaches lineares Modell (lineare Regression) verwendet, welches mit der Methode der kleinsten Quadrate bestimmt wird in der Form:

Y=\alpha +\beta X+\varepsilon _{t}

.

Es ergeben sich

\varepsilon _{t}

als die Störgrößen der Regression. Diese bilden eine neue Zeitreihe und müssen hier stationär sein. Ein gängiger Test auf Stationarität ist der Dickey-Fuller-Test. Die abgebildeten Residuen sind hier nicht stationär, das Verfahren müsste abgebrochen werden.

Zur Bestimmung der kurzfristigen Abweichungen von der langfristigen Beziehung wird eine neue Regression benötigt. Zuerst werden die ersten Differenzen $\Delta X$ und $\Delta Y$ der Zeitreihen $X$ und $Y$ gebildet. Sind die originalen Zeitreihen $X$ und $Y$ kointegriert, müssen die ersten Differenzen stationär sein. Es folgt eine weitere lineare Regression unter Verwendung der Residuen aus der langfristigen Beziehung (deshalb der Name Fehlerkorrekturmodell) und den beiden ersten Differenzen als erklärende Variable in der Form:

\Delta Y=\gamma +\phi \Delta X+\chi \varepsilon _{t-1}+u_{t}

.

Die Darstellung ist ebenfalls in Matrixschreibweise möglich. Das populärste Verfahren zur Schätzung eines Vektor-Fehlerkorrekturmodells geht zurück auf Johansen und Juselius (1988) und definiert das Modell wie folgt:

\Delta Z_{t}=\Pi \cdot Z_{t-1}+\sum _{i=1}^{k-1}\Gamma _{i}\Delta Z_{t-i}+u_{t}

.

Hierbei stellt $Z$ den Vektor der endogenen Variablen dar, der erste Teil der Summe enthält die Langfristdynamik in Form der Matrix $\Pi$ , die den Kointegrationsvektor enthält, der zweite Teil die Vektoren $\Gamma _{i}$ , die die Kurzfristdynamik beschreiben. Es ist möglich in die Langfristbeziehung eine Konstante und/oder einen deterministischen Trend zu integrieren.[1][2]

Umsetzung

Software jMulti

Einzelnachweise

Kirchgässner, Gebhard., Wolters, Jürgen., Hassler, Uwe.: Introduction to Modern Time Series Analysis. 2nd ed Auflage. Springer, Berlin 2013, ISBN 978-3-642-33436-8, S. 226.
Helmut Lütkepohl, Markus Krätzig, 1974-: Applied time series econometrics. Cambridge University Press, Cambridge, UK 2004, ISBN 0-511-20844-8, S. 89.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Kirchgässner, Gebhard., Wolters, Jürgen., Hassler, Uwe.: Introduction to Modern Time Series Analysis. 2nd ed Auflage. Springer, Berlin 2013, ISBN 978-3-642-33436-8, S. 226.

[2] Helmut Lütkepohl, Markus Krätzig, 1974-: Applied time series econometrics. Cambridge University Press, Cambridge, UK 2004, ISBN 0-511-20844-8, S. 89.