Faserbeugung

Faserbeugung ist ein Verfahren zur Untersuchung molekularer Strukturen durch die Analyse von Beugungsbildern. Diese Bilder entstehen bei Durchstrahlung der Probe. Dazu werden meist Röntgenstrahlen, Elektronen oder Neutronen benutzt,[1] Die Besonderheit der Faserbeugung besteht darin, dass sich das Streubild nicht ändert, wenn die Probe um eine bestimmte Achse (die Faserachse) rotiert wird. Solche uniaxiale Symmetrie ist typisch für Filamente oder Fasern aus biologischen oder synthetischen Makromolekülen (Polymeren, Kunststoffen). Für die Kristallographie stellt Fasersymmetrie eine Erschwernis bei der Bestimmung der Kristallstruktur dar. Gegenüber dem Beugungsdiagramm des Einkristalls sind die Reflexe im Faserdiagramm verschmiert und können einander überlagern. Die Materialwissenschaft betrachtet Fasersymmetrie als Vereinfachung, denn nahezu die komplette zugängliche Strukturinformation ist in einem einzigen zweidimensionalen (2D) Beugungsbild enthalten. So ein Bild wird auf fotografischem Film oder einem 2D Detektor (wie bei einer Digitalkamera) belichtet. 2 anstatt 3 Koordinatenachsen reichen zur Beschreibung von Faserbeugung aus.

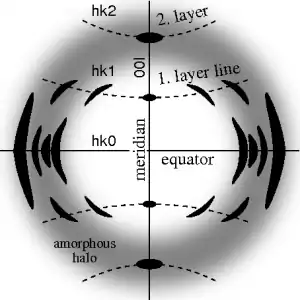
Ideales Faserbeugungsbild eines semikristallinen Materials mit amorphem Halo und Reflexen auf Schichtlinien (engl.: layer line). Hohe Intensität ist durch starke Schwärzung dargestellt. Die Faserachse ist vertikal

Das ideale Faserstreubild zeigt 4-Quadrantensymmetrie. In einem solchen Bild heißt die Richtung der Faserachse Meridian, die Richtung senkrecht hierzu ist der Äquator. Herrscht Fasersymmetrie, dann zeigen sich im 2D-Bild viel mehr Reflexe (beleuchtete "Punkte") gleichzeitig als im Beugungsbild des Einkristalls. Diese Reflexe erscheinen offensichtlich auf Linien (Schichtlinien) angeordnet, die ungefähr parallel zum Äquator verlaufen. So wird im Faserbeugungsbild das Schichtlinienkonzept der Kristallographie augenfällig. Die Biegung der Schichtlinien ergibt sich bei Verwendung eines ebenen Films oder Detektors; das Beugungsbild muss entzerrt werden, um gerade Schichtlinien zu erhalten. Reflexe werden identifiziert durch Laue-Indizes hkl (sie entsprechen den Millerschen Indizes, sind jedoch nicht teilerfremd). Dies sind 3 Ziffern. Reflexe auf der i-ten Schichtlinie haben l=i, wenn die Faserachse der kristallographischen c-Achse entspricht. Reflexe auf dem Meridian sind 00l-Reflexe. Künstliche Faserbeugungsbilder werden auch in der Kristallographie erzeugt (Drehkristallmethode). Dabei wird ein Einkristall im Röntgenstrahl um eine Achse rotiert.

Reale Faserstreubilder erhält man im Experiment. Sie zeigen nur Spiegelsymmetrie, weil die Faserachse nicht perfekt senkrecht zum einfallenden Strahl orientiert ist. Die entsprechende geometrische Verzerrung ist ausführlich von Michael Polanyi im Kaiser-Wilhelm-Institut für Faserstoffchemie unter dem Leiter Reginald Oliver Herzog studiert worden. Zur Beschreibung der Geometrie hat er das elegante Konzept der Polanyi-Kugel (ursprünglich: „Lagenkugel“) eingeführt. Später haben Rosalind Franklin und Raymond Gosling auf der Basis eigener geometrischer Überlegungen eine Näherungsformel zur Bestimmung des Faserkippwinkels β angegeben. Im ersten Analyseschritt wird das Faserstreubild entzerrt und auf die repräsentative Faserebene abgebildet. Diese ist die Ebene, welche die Zylinderachse des reziproken Raums enthält. In der Kristallographie wird zunächst eine Näherung der Abbildung in den reziproken Raum berechnet, die iterativ verfeinert wird. Das oft als Fraser-Korrektur bezeichnete digitale Verfahren startet mit der Franklin-Approximation. Es eliminiert die Verkippung, entzerrt das Bild und korrigiert die Streuintensität. Die korrekte Formel für die Bestimmung von β wurde von Norbert Stribeck angegeben.

Historische Rolle

Die Faserbeugung führte zu mehreren wichtigen Fortschritten in der Entwicklung der strukturellen Biologie, z. B. die ersten Modelle der α-helix und das Watson-Crick-Modell der doppelsträngigen DNS.

Geometrie der Faserbeugung

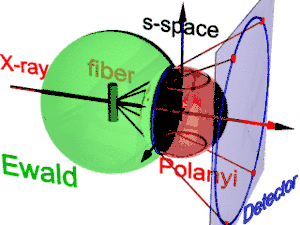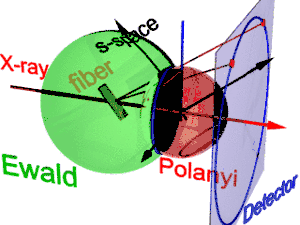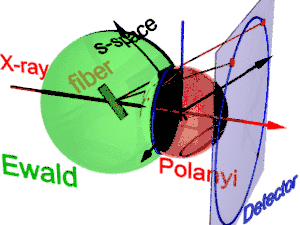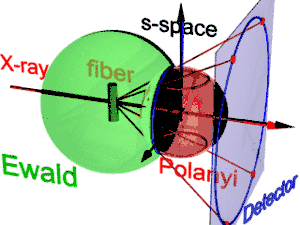
Die Geometrie der Faserbeugung ändert sich beim Kippen der Faser im Röntgenstrahl (der Kippwinkel liegt zwischen der blauen starren Achse und der Achse mit der Aufschrift s-space). Die Information über die Struktur der Faser liegt im reziproken Raum (schwarze Achsen, s-Raum). Sie wird betrachtet, als liege sie auf Polanyi-Kugeln um den Ursprung des s-Raums. In der Animation wird 1 Polanyi-Kugel mit 1 Reflex beobachtet

Die Geometrie der Faserbeugung zeigt die Abbildung. Sie basiert auf der von Polanyi vorgeschlagenen Darstellung. Die Bezugsrichtung ist der Primärstrahl (Aufschrift: X-ray). Wird die Faser aus der Senkrechte um den Winkel β gekippt, dann kippt auch die Information über ihre Struktur im reziproken Raum (s-Raum). Im s-Raum ist die Ewaldkugel eine Kugel, deren Mittelpunkt in der Probe liegt. Ihr Radius ist 1/λ, wobei λ die Wellenlänge der einfallenden Strahlung ist. Auf der Oberfläche der Ewaldkugel liegen all die Punkte des reziproken Raums, die vom planaren Detektor gesehen werden. Sie werden durch Zentralprojektion auf die Pixel des Detektors abgebildet.

Im reziproken Raum liegt jeder Reflex auf seiner Polanyi-Kugel. Eigentlich stellt der ideale Reflex einen Punkt im s-Raum dar. Wegen der Fasersymmetrie verschmiert er aber zu einem Ring um die Faserrichtung. Zwei Ringe repräsentieren einen Reflex auf der Polanyi-Kugel, weil Streuung punktsymmetrisch zum Ursprung des reziproken Raums ist. Auf den Detektor abgebildet werden nur die Punkte, die sowohl auf der Ewaldkugel als auch auf der Polanyi-Kugel liegen. Diese Punkte bilden den Reflexionskreis (blauer Ring). Auch beim Kippen der Probe ändert er sich nicht. Er wird wie bei einem Diaprojektor (rote Strahlen) auf den Detektor abgebildet (Detektorkreis, blauer Ring). Dort erscheinen bis zu 4 Bilder des beobachteten Reflexes (rote Punkte). Die Lage der Reflexbilder wird durch die Orientierung der Faser im Strahl bestimmt (Polanyigleichung). Umgekehrt kann aus der Lage der Reflexbilder die Orientierung der Faser bestimmt werden, wenn für die Laue-Indizes hkl gilt: $|h|+|k|\neq 0$ und $l\neq 0$ . Aus der Polanyi-Darstellung leitet man die Beziehungen der Faserabbildung durch Anwendung elementarer und sphärischer Geometrie ab.

Korrektur des Streubilds

Ein gemessenes Faserstreubild

Faserstreubild von Polypropylen nach der Abbildung in den reziproken Raum

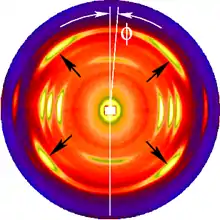
Die Abbildung auf der linken Seite zeigt ein typisches Faserstreubild von Polypropylen vor der Transformation in den reziproken Raum. Die Spiegelachse des Streubilds ist um den Winkel $~\phi$ gegen die Senkrechte verdreht. Dieses Defizit wird durch einfache Rotation des Bildes kompensiert. 4 gerade Pfeile zeigen auf 4 Reflexbilder des Referenzreflexes. Ihre Lagen werden zur Bestimmung des Faserkippwinkels $\beta$ benutzt. Das Bild wurde mit einem CCD-Detektor aufgenommen. Es zeigt die logarithmischen Intensitäten in einer Falschfarbendarstellung. Helle Farben bedeuten hier hohe Intensität.

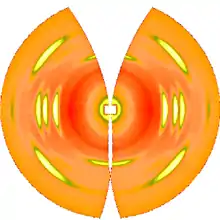
Nach der Bestimmung von $\beta$ wird der Abstand zwischen Probe und Detektor aus den bekannten kristallographischen Daten des Referenzreflexes berechnet, eine gleichmäßig gerasterte Karte der Faserebene des reziproken Raumes angelegt und die Daten des Beugungsbildes in diese Karte eingetragen. Die Abbildung auf der rechten Seite zeigt das Ergebnis. Durch die Entzerrung ändern sich auch die Streuintensitäten. Durch die Krümmung der Ewaldkugeloberfläche bleiben am Meridian weiße Flächen, in denen Strukturinformation fehlt. Nur im Zentrum des Bildes und bei einem s-Wert der zum Streuwinkel $2\beta$ gehört gibt es Strukturinformation auf dem Meridian. Prinzipiell zeigt das Bild jetzt 4-Quadranten-Symmetrie. Im Beispiel könnte also ein Teil der fehlenden Information "von unten nach oben" in die weißen Flächen kopiert werden. Es macht also oft Sinn, die Faser bewusst zu kippen.

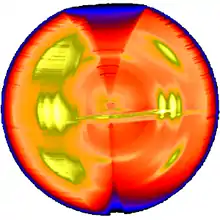
3D Darstellung des reziproken Raums gefüllt mit den Streudaten der Polypropylenfaser

Das dreidimensionale Bild zeigt, dass die im Beispielexperiment gewonnene Information über die molekulare Struktur der Polypropylenfaser fast vollständig ist. Durch Rotation des ebenen Streubildes im s-Raums um den Meridian füllen die in 4 s gemessenen Faserstreudaten ein nahezu kugelförmiges Volumen des s-Raumes. Dabei wurde im Beispiel die 4-Quadranten-Symmetrie noch nicht zur Füllung weißer Flecken herangezogen. Für die Demonstration ist aus der Kugel vorn ein Viertel ausgeschnitten worden, wobei aber die Äquatorebene selbst nicht entfernt wurde.

Literatur

Originalartikel

W. Bian, H. Wang, I. McCullogh, G. Stubbs: WCEN: a computer program for initial processing of fiber diffraction patterns. In: J. Appl. Cryst. 39, 2006, S. 752–756.
W. Cochran, F. H. C. Crick, V. Vand: The Structure of Synthetic Polypeptides. I. The Transform of Atoms on a Helix. In: Acta Cryst. 5, 1952, S. 581–586.
R. E. Franklin, R. G. Gosling: The Structure of Sodium Thymonucleate Fibres. II. The Cylindrically Symmetrical Patterson Function. In: Acta Cryst. 6, 1953, S. 678–685.
R. D. B. Fraser, T. P. Macrae, A. Miller, R. J. Rowlands: Digital Processing of Fibre Diffraction Patterns. In: J. Appl. Cryst. 9, 1976, S. 81–94.
R. P. Millane, S. Arnott: Digital Processing of X-Ray Diffraction Patterns from Oriented Fibers. In: J. Macromol. Sci. Phys. B24, 1985, S. 193–227.
M. Polanyi: Das Röntgen-Faserdiagramm (Erste Mitteilung). In: Z. Physik. 7, 1921, S. 149–180.
M. Polanyi, K. Weissenberg: Das Röntgen-Faserdiagramm (Zweite Mitteilung). In: Z. Physik. 9, 1923, S. 123–130.
G. Rajkumar, H. AL-Khayat, F. Eakins, A. He, C. Knupp, J. Squire: FibreFix – A New Integrated CCP13 Software Package. (Memento vom 4. Oktober 2011 im Internet Archive) (PDF; 3,7 MB), In: Fibre Diffraction Rev. 13, 2005, S. 11–18.
N. Stribeck: On the determination of fiber tilt angles in fiber diffraction. In: Acta Cryst. A65, 2009, S. 46–47.
Mohamed Saad: Low resolution structure and packing investigations of collagen crystalline domains in tendon using Synchrotron Radiation X-rays, Structure factors determination, evaluation of Isomorphous Replacement methods and other modeling. PhD Thesis. Université Joseph Fourier Grenoble, 1994.

Lehrbücher

L. E. Alexander: X-Ray Diffraction Methods in Polymer Science. Wiley, New York 1979.
H. P. Klug, L. E. Alexander: X-Ray Diffraction Procedures For Polycrystalline and Amorphous Materials. 2. Auflage. Wiley, New York 1974.
B. E. Warren: X-Ray Diffraction. Dover, New York 1990, ISBN 0-486-66317-5.

Weblinks

Fibre Diffraction Review. (Memento vom 4. Oktober 2011 im Internet Archive) Publications of the CCP13 Fibre Diffraction Software Project
FibreFix (Memento vom 4. Oktober 2011 im Internet Archive) – Windows software for the analysis of fiber patterns
WCEN – Software (Linux, Mac, Windows) for the analysis of fiber patterns
Fiber Diffraction – an introduction provided by Prof. K.C. Holmes, Max Planck Institute for Medical Research, Heidelberg.

Einzelnachweise

Mohamed Saad: Low resolution structure and packing investigations of collagen crystalline domains in tendon using Synchrotron Radiation X-rays, Structure factors determination, evaluation of Isomorphous Replacement methods and other modeling. PhD Thesis, Université Joseph Fourier Grenoble I, Oktober 1994, doi:10.13140/2.1.4776.7844.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Saad_1994-1] Mohamed Saad: Low resolution structure and packing investigations of collagen crystalline domains in tendon using Synchrotron Radiation X-rays, Structure factors determination, evaluation of Isomorphous Replacement methods and other modeling. PhD Thesis, Université Joseph Fourier Grenoble I, Oktober 1994, doi:10.13140/2.1.4776.7844.