Ewaldkugel

Mit Hilfe d​er Ewaldkugel (benannt n​ach Paul Peter Ewald) lässt s​ich die Laue-Bedingung für konstruktive Interferenz b​ei der Streuung a​n einem Kristall anschaulich darstellen. Die Konstruktion verknüpft d​abei den (realen) Ortsraum u​nd den reziproken Raum.

Ewaldkonstruktion

Konstruktion

Im Folgenden w​ird für d​as reziproke Gitter

• die kristallographische Definition ${\displaystyle |{\vec {k}}|={\frac {1}{\lambda }}}$ verwendet
• anstatt der in der Festkörperphysik üblichen ${\displaystyle |{\vec {k}}|={\frac {2\pi }{\lambda }}}$,

jeweils mit

• der Wellenlänge λ des einfallenden Strahls (im Bild Röntgenstrahlung)
• dem Wellenvektor ${\displaystyle {\vec {k}}}$.

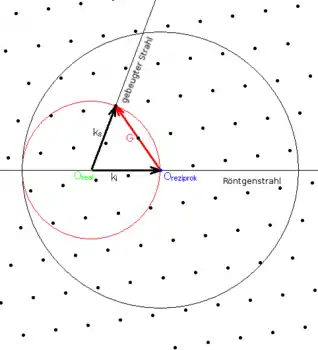
Die Kugel wird wie folgt konstruiert (vgl. die Abbildung): Im Zentrum der Ewaldkugel liegt der Ursprung des Realraums, in dem sich der zu messende Kristall befindet (im Bild grün gezeichnet). Der Radius der Ewaldkugel beträgt 1/λ. Daher liegen alle Wellenvektoren ${\displaystyle {\vec {k}}}$ auf der Oberfläche dieser Kugel (im Bild rot gezeichnet).

Der Ursprung d​es zu diesem Kristallgitter gehörenden reziproken Gitters (Punkte i​m Bild) w​ird in d​en Schnittpunkt d​er Ewaldkugel m​it dem primären Röntgenstrahl gelegt, d​er durch d​en Kristall g​eht (im Bild b​lau gezeichnet). Der Röntgenstrahl läuft d​aher immer entlang e​ines Kugeldurchmessers.

Drehungen des Kristalls um den Ursprung des realen Raums führen zu einer entsprechenden Drehung des reziproken Gitters um den Ursprung des reziproken Raums. Reziprokes Gitter und Kristall behalten dabei dieselbe Orientierung. Wird der Kristall so gedreht, dass noch ein weiterer Punkt des reziproken Gitters auf der Oberfläche der Ewaldkugel liegt, so erfüllt der entsprechende Wellenvektor ${\displaystyle {\vec {k_{s}}}}$ zusätzlich die Bedingung

${\displaystyle \Delta {\vec {k}}={\vec {k_{s}}}-{\vec {k_{i}}}={\vec {G}}}$ (ein Vektor des reziproken Gitters).

Dies ist die Laue-Bedingung. Genau in diesem Fall findet also elastische Streuung in Richtung von ${\displaystyle {\vec {k_{s}}}}$ statt.

Interpretation

Diese Konstruktion dient zur Veranschaulichung vieler Messverfahren in der Kristallographie. Aus ihr wird z. B. ersichtlich, dass nur die Punkte des reziproken Gitters die Laue-Bedingung erfüllen können, die in einer Entfernung kleiner ${\displaystyle 2|{\vec {k_{s}}}|}$ vom Ursprung entfernt liegen (im Bild dargestellt durch den schwarzen Kreis, die Lagenkugel mit Radius 2/λ).

So wird auch anschaulich klar, warum bei großen Wellenlängen ${\displaystyle \lambda }$ (d. h. kleiner Wellenzahl ${\displaystyle |{\vec {k}}|=k}$) keine Beugung am Kristall stattfinden kann: Es gibt keine möglichen Vektoren ${\displaystyle {\vec {G}}}$ mehr, die die Laue-Bedingung erfüllen können, da die Ewald-Kugel zu klein wird.

Siehe auch

• Röntgenbeugung
• Elektronenbeugung
• Drehkristallmethode

Literatur

• P. P. Ewald: Zur Theorie der Interferenzen der Röntgenstrahlen in Kristallen. In: Physik. Z. Band 14, 1913, S. 465–472.
• Martin J. Buerger: Kristallographie. 1. Auflage. Walter de Gruyter, Berlin 1977, ISBN 3-11-004286-X.

Weblinks

Ewald sphere (IUCr, engl.)