Faktorisierungsmethode von Fermat

Die Faktorisierungsmethode von Fermat ist ein Algorithmus aus dem mathematischen Teilgebiet Zahlentheorie. Er berechnet zu einer ungeraden, zusammengesetzten Zahl ${\displaystyle n}$ zwei Teiler ${\displaystyle a}$ und ${\displaystyle b}$, für die ${\displaystyle a\cdot b=n}$ gilt.

Die Faktorisierungsmethode v​on Fermat h​at nur d​ann eine g​ute Laufzeit, w​enn sich d​ie zu zerlegende Zahl a​ls Produkt annähernd gleich großer Faktoren darstellen lässt. Sie bildet z​udem die Grundlage allgemeiner Faktorisierungsverfahren für große Zahlen, d​ie in d​er Regel e​ine bessere Laufzeit aufweisen.

Pierre d​e Fermat beschrieb d​iese heute n​ach ihm benannte Faktorisierungsmethode 1643 i​n einem Brief, d​er vermutlich a​n Mersenne o​der Frénicle d​e Bessy adressiert war. In diesem Brief demonstrierte e​r das Verfahren, i​ndem er d​ie Primfaktorzerlegung v​on 2.027.651.281 berechnete.[1] Einige Historiker vermuten aber, d​ass die Methode s​chon früher bekannt war.

Algorithmus

Sei ${\displaystyle n}$ die zu faktorisierende ungerade Zahl. Die Faktorisierungsmethode von Fermat berechnet nacheinander die Werte

${\displaystyle \left(\left\lceil {\sqrt {n}}\right\rceil \right)^{2}-n}$

${\displaystyle \left(\left\lceil {\sqrt {n}}\right\rceil +1\right)^{2}-n}$

${\displaystyle \left(\left\lceil {\sqrt {n}}\right\rceil +2\right)^{2}-n}$

${\displaystyle \vdots }$

Dabei bezeichnet ${\displaystyle \left\lceil {\sqrt {n}}\right\rceil }$ die kleinste ganze Zahl größer oder gleich ${\displaystyle {\sqrt {n}}}$.

Dies w​ird fortgesetzt, b​is einer dieser Werte e​ine Quadratzahl ist:

${\displaystyle \left(\left\lceil {\sqrt {n}}\right\rceil +z\right)^{2}-n=x^{2}-n=y^{2}}$

Aufgrund d​er dritten binomischen Formel g​ilt dann

${\displaystyle n=x^{2}-y^{2}=(x+y)(x-y)=a\cdot b.}$

Dabei erhält man diejenige Zerlegung von ${\displaystyle n}$, für die das Verhältnis ${\displaystyle a/b}$ (mit ${\displaystyle a\geq b}$) am kleinsten ist.

Das folgende Nassi-Shneiderman-Diagramm z​eigt den Ablauf d​es Algorithmus, w​ie er s​chon von Fermat angewandt wurde. Dabei w​ird das wiederholte Quadrieren d​er obigen Beschreibung vermieden. Die einzelnen Werte werden d​azu mittels d​er ersten binomischen Formel a​us ihrem jeweiligen Vorgänger berechnet:

${\displaystyle \left(s+1\right)^{2}-n=s^{2}+2s+1-n}$

Berechne ${\displaystyle x=\left\lceil {\sqrt {n}}\right\rceil }$
Berechne ${\displaystyle r=x^{2}-n}$
solange ${\displaystyle r}$ keine Quadratzahl
	${\displaystyle r\leftarrow r+2x+1}$
	${\displaystyle x\leftarrow x+1}$
Berechne ${\displaystyle y={\sqrt {r}}}$
Berechne ${\displaystyle a=x+y}$
Berechne ${\displaystyle b=x-y}$

Anmerkung

Indem man die letzten beiden Ziffern von ${\displaystyle r}$ überprüft, kann man in vielen Fällen ausschließen, dass ${\displaystyle r}$ eine Quadratzahl ist. Bei einer Quadratzahl gibt es nur 22 Möglichkeiten: 00, x1, x4, 25, y6 und x9, wobei x für eine gerade und y für eine ungerade Ziffer steht. Man kann also bei vielen Zahlen durch Überprüfung der letzten beiden Ziffern ausschließen, dass es Quadratzahlen sind. Auch Fermat nutzte diese Eigenschaft der Quadratzahlen. Dies funktioniert auch mit anderen quadratischen Resten, etwa Zweierpotenzen, die sich auf einer klassischen Computerarchitektur leicht überprüfen lassen. Diese Idee kann man verallgemeinern, indem man nicht nur die Quadrate, sondern die quadratische Gleichung in zwei Variablen bezüglich ihrer Reste untersucht:

${\displaystyle x^{2}=y^{2}+n{\bmod {q}}}$

Wegen der Eigenschaft ${\displaystyle (-x)^{2}=x^{2}}$ kann es für ${\displaystyle x}$ maximal ${\displaystyle (q+1)/2}$ mögliche Reste geben, wenn ${\displaystyle n}$ und ${\displaystyle q}$ teilerfremd sind. Durch Kombinieren der Restklassen bezüglich verschiedener Primzahlen (bzw. kleiner Primzalpotenzen) lassen sich die Lösungen für ${\displaystyle x}$ pro verwendeter Restklasse jeweils nahezu halbieren.

Beispiele

Beispiel mit vielen Iterationen

Man möchte Faktoren der Zahl 1729 bestimmen. Die Wurzel aus 1729 beträgt etwa 41,6. Die erste Zahl ${\displaystyle x}$, für die man ${\displaystyle r}$ berechnet, ist also die 42.

${\displaystyle x}$	${\displaystyle r=x^{2}-n}$	${\displaystyle 2x+1}$
42	35	85
43	120	87
44	207	89
45	296	91
46	387	93
47	480	95
48	575	97
49	672	99
50	771	101
51	872	103
52	975	105
53	1080	107
54	1187	109
55	1296 = 36^2

Man kann nun sofort die beiden Faktoren von ${\displaystyle n}$ berechnen:

${\displaystyle y={\sqrt {r}}=36}$

${\displaystyle a=x+y=55+36=91}$

${\displaystyle b=x-y=55-36=19}$

Eine Zerlegung v​on 1729 lautet damit:

${\displaystyle 1729=19\cdot 91}$

Beispiel mit wenigen Iterationen

Am Beispiel der Zahl 290377 sieht man, dass es Zahlen gibt, bei der die Faktorisierungsmethode von Fermat sehr schnell eine Zerlegung berechnet. Die Wurzel aus 290377 beträgt etwa 538,9. Die nächste ganze Zahl ${\displaystyle x}$ ist somit 539. Es zeigt sich, dass ${\displaystyle r}$ schon im ersten Schritt eine Quadratzahl ist:

${\displaystyle r=x^{2}-n=539^{2}-290377=144=12^{2}}$

Man kann nun sofort die beiden Faktoren von ${\displaystyle n}$ berechnen:

${\displaystyle y={\sqrt {r}}={\sqrt {144}}=12}$

${\displaystyle a=x+y=539+12=551}$

${\displaystyle b=x-y=539-12=527}$

Eine Zerlegung v​on 290377 lautet damit

${\displaystyle 290377=551\cdot 527}$

Weder ${\displaystyle 551=19\cdot 29}$ noch ${\displaystyle 527=17\cdot 31}$ sind Primzahlen. Aber man kann den Algorithmus erneut auf 551 und 527 anwenden, um die vollständige Primfaktorzerlegung zu erhalten.

Grafisches Beispiel

Alle ganzzahligen Teiler können als Punkte in einer Teilerfläche dargestellt werden. Die ${\displaystyle x}$-Achse gibt jeweils die Teilerwerte wieder, die ${\displaystyle y}$-Achse entspricht einem ganzzahligen Zahlenstrahl (zur besseren Nachvollziehbarkeit werden im Beispiel die ${\displaystyle x}$- und ${\displaystyle y}$-Achse im Verhältnis 1 zu 16 skaliert).

Die Teilerpunkte i​n einer Teilerfläche besitzen u. a. folgende Eigenschaften:

• Alle Teilerpunkte der Teilerfläche können einer negativen Parabel der Form ${\displaystyle y=-x^{2}+px}$ zugeordnet werden.

• Alle komplementären Teilerpaare einer Zahl befinden sich auf einer gemeinsamen Parabel.

• Die Addition zweier komplementärer Teiler einer Zahl liefert den Koeffizienten ${\displaystyle p}$ der gemeinsamen negativen Parabel.

Beispiel:

${\displaystyle 145=1\cdot 145=5\cdot 29}$

Fermat's factorization in the divisor plane

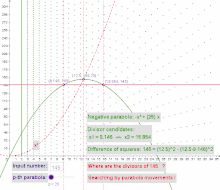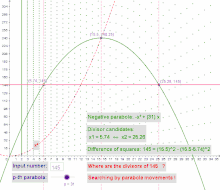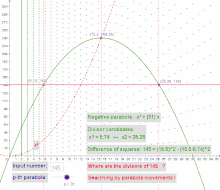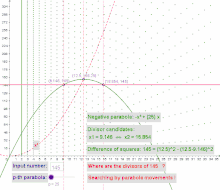
Die komplementären Teilerpaare von ${\displaystyle 145}$ sind die trivialen Teiler ${\displaystyle 1\cdot 145}$ und die nicht-trivialen Teiler ${\displaystyle 5\cdot 29}$.

Die Schnittpunkte von Parabeln der Form ${\displaystyle y=-x^{2}+px}$ mit der Parallelen zur ${\displaystyle x}$-Achse ${\displaystyle y=145}$ liefern somit Teilerkandidaten. Das Verschieben der Parabel liefert entweder die nicht-trivialen oder, im allerletzten Schritt, die trivialen Teiler einer Zahl.

Als erste negative Parabel mit einem Scheitelpunktwert größer ${\displaystyle 145}$ wird ${\displaystyle y=-x^{2}+25x}$ identifiziert (${\displaystyle p=\lceil ({\sqrt {1}}45)\cdot 2\rceil =25}$). Nach mehrfachem Verschieben werden die Teiler ${\displaystyle 5}$ und ${\displaystyle 29}$ mit der Parabel ${\displaystyle y=-x^{2}+(5+29)x=-x^{2}+34x}$ gefunden. Scheitelpunkt dieser Parabel ist ${\displaystyle S(17,289)}$.

Die Zahl ${\displaystyle 145}$ ist somit als Differenz der Quadrate ${\displaystyle 17^{2}-(17-5)^{2}=17^{2}-12^{2}=289-144}$ darstellbar. Die nicht-trivialen Teiler lassen sich über ${\displaystyle 17-12=5}$ und ${\displaystyle 17+12=29}$ berechnen.

Da Parabeln der Form ${\displaystyle y=-x^{2}+(2p+1)x}$ ausschließlich komplementäre Teiler zu geraden Zahlen liefern werden sie in Fermat's Methode nicht berücksichtigt.

Funktionsweise

Die Faktorisierungsmethode von Fermat sucht nach zwei Quadratzahlen ${\displaystyle x^{2}}$ und ${\displaystyle y^{2}}$, die die Gleichung ${\displaystyle x^{2}-n=y^{2}}$ erfüllen. Auf Grund der 3. binomischen Formel ist dann

${\displaystyle n=x^{2}-y^{2}=(x+y)(x-y)}$

und ${\displaystyle a=x+y}$ und ${\displaystyle b=x-y}$ sind die gesuchten Teiler von ${\displaystyle n}$. Das Fermatsche Verfahren findet dabei genau diejenige Teiler ${\displaystyle a}$ und ${\displaystyle b}$, die am nächsten zur Wurzel von ${\displaystyle n}$ liegen.

Es stellt sich die Frage, ob immer zwei Quadratzahlen ${\displaystyle x^{2}}$ und ${\displaystyle y^{2}}$ existieren, die obige Gleichung erfüllen. Wäre dies nicht der Fall, würde der Algorithmus in eine Endlosschleife geraten. Im Folgenden sei ${\displaystyle n}$ eine ungerade, zusammengesetzte Zahl, wie bei der Faktorisierungsmethode von Fermat vorausgesetzt. Dann ist ${\displaystyle n}$ das Produkt zweier ungerader Zahlen ${\displaystyle a}$ und ${\displaystyle b}$ und damit sind auch

${\displaystyle x={\frac {a+b}{2}}}$ und ${\displaystyle y={\frac {a-b}{2}}}$

ganze Zahlen. Durch eine einfache Rechnung unter Anwendung der binomischen Formeln zeigt sich, dass ${\displaystyle x^{2}-y^{2}=n}$ ist:

${\displaystyle x^{2}-y^{2}=\left({\frac {a+b}{2}}\right)^{2}-\left({\frac {a-b}{2}}\right)^{2}={\frac {a^{2}+2ab+b^{2}}{4}}-{\frac {a^{2}-2ab+b^{2}}{4}}=ab=n}$

Die Zahl ${\displaystyle n}$ lässt sich somit immer als Differenz zweier Quadratzahlen darstellen.

Laufzeitanalyse

Das Verfahren gelangt in wenigen Iterationen zu einer Lösung, wenn sich eine Zahl in zwei annähernd gleich große Faktoren zerlegen lässt. Wir können den größeren Faktor in der Form ${\displaystyle a=\left(1+\epsilon \right){\sqrt {n}}}$ mit einem ${\displaystyle \epsilon >0}$ schreiben. Ist der Wert ${\displaystyle \epsilon }$ sehr viel kleiner als 1, ergibt sich für die Zahl der notwendigen Iterationen annähernd ${\displaystyle {\frac {{\epsilon }^{2}}{2}}{\sqrt {n}}}$. In diesem Fall ist das Verfahren sehr viel schneller als die Probedivision.

Falls die Faktoren jedoch weit auseinander liegen, braucht auch dieses Verfahren sehr viele Iterationen. Im schlechtesten Fall bei ${\displaystyle n=3p}$, wobei ${\displaystyle p}$ eine Primzahl ist, benötigt dieses Verfahren ${\displaystyle \Omega (n)}$ viele Iterationen.

Erweiterung: Faktorisierung eines Vielfachen

Um die schlechte Laufzeit für Zahlen zu umgehen, die nicht das Produkt zweier annähernd gleich großer Faktoren sind, kann man die Faktorisierungsmethode für ein Vielfaches ${\displaystyle n'=k\cdot n}$ der ursprünglichen Zahl ${\displaystyle n}$ durchführen. Die größten gemeinsamen Teiler zwischen ${\displaystyle n}$ und je einem der berechneten Faktoren ${\displaystyle a'}$ und ${\displaystyle b'}$ von ${\displaystyle n'}$ liefern anschließend jeweils einen Teiler von ${\displaystyle n}$.

Als Beispiel betrachten wir die Zahl 1729, bei der die normale Faktorisierungsmethode 14 Schritte benötigt. Die Zahl ${\displaystyle 120\cdot 1729=207480}$ kann bereits nach zwei Iterationen in die Faktoren 420 und 494 zerlegt werden. Ein Teiler von 1729 kann als größter gemeinsamer Teiler berechnet werden:

${\displaystyle \operatorname {ggT} (1729,420)=7}$

Mit ${\displaystyle {\frac {1729}{7}}=247}$ hat man eine Faktorisierung der Zahl 1729:

${\displaystyle 1729=7\cdot 247}$

Es stellt sich nun das Problem, einen geeigneten Faktor ${\displaystyle k}$ zu finden. Russell Sherman Lehman hat 1974 mit der Faktorisierungsmethode von Lehman ein Verfahren entwickelt, das solche ${\displaystyle k}$ findet. Dadurch verkürzt sich die Laufzeit auf ${\displaystyle O(n^{\frac {1}{3}}\log \log n)}$.

Faktorisierungsmethode von Fermat als Primzahltest

Die Faktorisierungsmethode von Fermat kann als Primzahltest verwendet werden,[2] auch wenn dies nicht besonders effizient ist. Aus der Laufzeitanalyse ist bekannt, dass die ungünstigste Eingabe für den Algorithmus eine Zahl der Form ${\displaystyle n=3p}$ ist (${\displaystyle p}$ ist dabei eine Primzahl). In diesem Fall ist

${\displaystyle x={\frac {3+p}{2}}={\frac {3+{\tfrac {n}{3}}}{2}}={\frac {9+n}{6}}}$

Lässt man nun als Eingabe ${\displaystyle n}$ des Algorithmus beliebige ungerade Zahlen zu und ist keine der Zahlen

${\displaystyle \left(\lceil {\sqrt {n}}\rceil \right)^{2}-n,\left(\lceil {\sqrt {n}}\rceil +1\right)^{2}-n,\dotsc ,\left({\frac {9+n}{6}}\right)^{2}-n}$

eine Quadratzahl, so ist ${\displaystyle n}$ eine Primzahl.

Literatur

• Hans Riesel: Prime Numbers and Computer Methods for Factorization. 2. Auflage. Birkhäuser, Boston 1994, ISBN 0-8176-3743-5.
• Donald E. Knuth: The Art of Computer Programming. Volume 2. Seminumerical Algorithms. 3. Auflage. Addison-Wesley, 1998, ISBN 0-201-89684-2.

Weblinks

• Eric W. Weisstein: Fermat’s Factorization Method. In: MathWorld (englisch).
• The Prime Glossary: Fermat’s method of factoring.
• Bruno Lehnen (GeoGebra-Materialien): Fermat's factorization in the divisor plane.

Einzelnachweise

1. Leonard E. Dickson: History of the Theory of Numbers. Volume 1. Divisibility and Primality. Dover Publications, 2005, ISBN 0-486-44232-2, S. 357.
2. Richard Crandall, Carl Pomerance: Prime Numbers. A Computational Perspective. 2. Auflage. Springer-Verlag, New York, 2005, ISBN 0-387-25282-7, S. 191–192.