Einstein-de-Haas-Effekt
Der Einstein-de-Haas-Effekt zeigt den Zusammenhang zwischen dem Ferromagnetismus und dem Drehimpuls von Elektronen. Er ist ein makroskopischer Nachweis des Spindrehimpuls der Elektronen. Der Effekt wurde 1908 von O. W. Richardson vorhersagt[1], allerdings in Bezug auf den Bahndrehimpuls, und so 1915 von Albert Einstein zusammen mit Wander Johannes de Haas auch nachgewiesen.[2][3]
Experiment
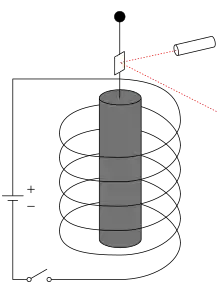
Ein dünner, magnetisierbarer Stab (z. B. aus Eisen, Nickel) hängt senkrecht an einem Torsionsfaden in einer senkrecht stehenden Magnetspule. Da das Magnetfeld zum Stab parallel und die ganze Anordnung rotationssymmetrisch ist, kann das Magnetfeld kein Drehmoment auf den Stab ausüben. Trotzdem beginnt er sich beim Einschalten oder Umpolen des Magnetfelds um die Aufhängerichtung zu drehen.
Deutung
Der gesamte Drehimpuls des Stabs setzt sich aus zwei Anteilen zusammen: ein Anteil entspricht der außen sichtbaren Drehbewegung, der andere Anteil ist die Summe der permanenten Drehimpulse der Elektronen. Diese sind normalerweise ungeordnet, ihre Summe also Null. Durch ihre Parallelstellung aber ergibt sich die makroskopische Magnetisierung. Wenn vor Einschalten des Magnetfelds der Stab in Ruhe und nicht magnetisiert ist, ist der Gesamtdrehimpuls Null, denn beide Anteile sind für sich Null. Da sich am Gesamtdrehimpuls Null durch das Einschalten nichts ändern kann, müssen beide Drehimpulsanteile stets entgegengesetzt gleich groß sein. Daher zeigt die sichtbare Drehbewegung, dass die Magnetisierung des Stabes mit einem bestimmten Drehimpuls verknüpft ist, der durch die Beobachtung der sichtbaren Drehbewegung messbar wird. Das gemessene Verhältnis des Magnetischen Moments des Stabes zu diesem Drehimpuls (das gyromagnetische Verhältnis) stimmt mit dem an einzelnen Elektronen beobachteten gyromagnetischen Verhältnis überein.
Die Umkehrung dieses Effektes ist der Barnett-Effekt.
Historisches
Der beobachtete Effekt ist nur klein, sodass man eine Resonanzschwingung verwendet, um ihn besser messbar zu machen. Dazu wird der Stab als Drehpendel mit einer bestimmten Resonanzfrequenz aufgebaut und in der Spule ein magnetisches Wechselfeld variabler Frequenz angelegt. Beim Durchstimmen der Frequenz zeigt sich an der Amplitude der Torsionsschwingung eine deutliche Resonanzkurve. Allerdings ist die quantitative Auswertung nicht einfach. Z. B. entsteht durch die ferromagnetische Hysterese im Stab die Komplikation, dass sich die Magnetisierung und damit auch der Drehimpuls nicht linear mit dem äußeren Feld ändern. Daher sind die erhaltenen Ergebnisse mit relativ großer Unsicherheit behaftet. Einstein und de Haas schätzten sie für ihre Messung auf ±10 %[2][3]. Das Experiment wurde in den folgenden 10 Jahren durch de Haas und andere Forscher mit verbesserten Aufbauten öfters wiederholt. Die Ergebnisse streuten mit einer Häufung bei etwa dem Doppelten des ursprünglichen Ergebnisses von Einstein und de Haas.[4][5]
Das von Einstein und de Haas ursprünglich veröffentlichte Ergebnis entsprach der damaligen Erklärung des Ferromagnetismus durch die Bewegung von Elektronen auf Kreisbahnen (Ampèresche Molekularstöme). Das nach den verbesserten Messungen eher doppelt so große magnetische Moment (bezogen auf den gleichen Drehimpuls) konnte im Rahmen der klassischen Physik und der damaligen Atomtheorien nur durch Beiträge bewegter positiver Ladungen in den Atomen erklärt werden. Erst 1925 wurde anhand von Atomspektren der Elektronenspin entdeckt, ein Eigendrehimpuls der Elektronen, für den es keine mechanische Erklärung gibt, und der ein genau verdoppeltes magnetisches Moment bewirkt.
Siehe auch
Literatur
- D. Meschede: Gerthsen Physik. 23. Auflage. Springer, Berlin, Heidelberg 2006, ISBN 978-3-540-25421-8, S. 395.
- Demtröder: Experimentalphysik, 4. Auflage, Bd. 3, S. 168
- H. Haken und H. C. Wolf: Atom- und Quantenphysik. Einführung in die experimentellen und theoretischen Grundlagen, Springer, Heidelberg 2000.
- Peter Galison: Theoretical predisposition in experimental physics: Einstein and the gyromagnetic experiments 1915–1925, Historical Studies in the Physical Sciences, Band 12, 1982, Heft 2
Weblinks
- Einstein-de-Haas-Effekt. (PDF; 1,5 MB) Beschreibung einer Versuchsdurchführung. Projektlabor TU-Berlin, 17. Januar 2001, S. 1–70, abgerufen am 26. November 2017.
- LP: Der Einstein-de-Haas-Effekt, Georg-August-Universität Göttingen
Einzelnachweise
- O. W. Richardson, A mechanical effect accompanying magnetization, Physical Review (Series I), Vol. 26, Issue 3, pp. 248–253 (1908).
- Albert Einstein, W. J. de Haas: Experimenteller Nachweis der Ampereschen Molekularströme. In: Verhandlungen der Deutschen Physikalischen Gesellschaft. Band 17, 1915, S. 152–170 (Volltext in Internet Archive BookReader - ab S 152-..).
- A. Einstein, W. J. de Haas: Experimental proof of the existence of Ampère's molecular currents. In: Koninklijke Akademie van Wetenschappen te Amsterdam (KNAW), Proceedings. Band 18, Nr. I, 1915, S. 696–711 (englisch, 'Digital Library' of the Dutch History of Science Web Center 2001 [PDF; 654 kB]).
- Emil Beck: Zum Experimentellen Nachweis der Ampereschen Molekularströme In: Annalen der Physik Bd. 60, 1919, S. 109–148
- Peter Galison: Theoretical predisposition in experimental physics: Einstein and the gyromagnetic experiments 1915-1925. In: Historical Studies in the Physical Sciences. Band 12, Nr. 2, 1982, S. 285—323, doi:10.2307/27757498.