Druckaufschmelzung

Unter Druckaufschmelzung versteht man den Effekt, dass man den Schmelzpunkt von Eis durch eine Erhöhung des Druckes herabsetzen kann. In der Glaziologie wird die durch den Auflagedruck überlagerter Massen herabgesetzte Schmelztemperatur von Eis Druckschmelzpunkt genannt, ein für temperierte Gletscher maßgeblicher Mechanismus, wobei auch bei den meisten Gebirgsgletschern die druckbedingte Herabsetzung der Schmelztemperatur nur geringfügig ist (< 1 K).

Phasendiagramm von H₂O

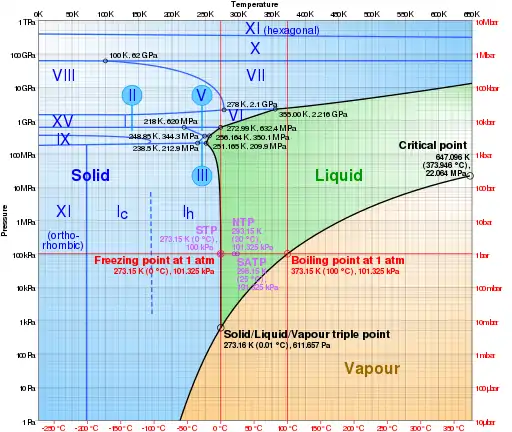
Pro zusätzlichem Bar erhöhtem Druck sinkt der Schmelzpunkt linear um ca. 0,0077 K, also bei einer Eisdicke von ca. 120 m um 0,1 K, was jedoch nur für kleine Drücke zutrifft. Bei hohen Drücken (> 500 bar, also ca. 5500 m) beschleunigt sich Abnahme des Schmelzpunktes nichtlinear, da die Dichte von Wasser am Gefrierpunkt zwar mit steigendem Druck nahezu linear steigt, die Dichte von Eis am Gefrierpunkt jedoch mit steigendem Druck immer langsamer steigt, bis sie oberhalb von etwa 150 MPa (1500 bar) konstant wird.[1]

Etwas exakter folgt aus der Clausius-Clapeyron-Gleichung die Beziehung

T_{\text{neu}}=T_{\text{start}}\cdot e^{\frac {\Delta p\cdot (v_{L}-v_{S})}{L}}

Hierbei sind:

$T_{\text{neu}}$ Der neue Schmelzpunkt
$T_{\text{start}}$ Der alte Schmelzpunkt beim Anfangsdruck.
$\Delta p$ Die Druckänderung
$v_{L},v_{S}$ Die spezifischen Volumina des Stoffes (L...flüssig, S...fest).
$L$ Die spezifische Schmelzwärme des Stoffes.

Sehr verbreitet ist die unzutreffende Ansicht, dass dieser Effekt beim Schlittschuhlauf ausschließlich durch den Druck der Kufen das Eis schmilzt und ein Wasserfilm entsteht, der das Gleiten der Kufen ermöglicht. Tatsächlich verursacht aber die Bewegung der Kufen auch Reibungswärme, die das Eis aufschmilzt und einen gleitfähigen Wasserfilm bildet.[2]

Der folgende Rechnungsgang demonstriert die Größenordnungen:

Für einen Schnelllauf-Schlittschuh mit – wie üblich – rechteckig plangeschliffener Kufe werde eine Dicke von 1,5 mm (= 0,15 cm) und eine Länge von 40 cm angenommen. Die Gesamtfläche beträgt somit 40 cm × 0,15 cm = 6 cm². Es ist allerdings darauf hinzuweisen, dass die Kufen quer zur Gleitrichtung ein Hohlprofil aufweisen[3]. Dabei befinden sich nur die beiden messerscharf geschliffenen Kante einer Kufe in Kontakt mit dem Medium "Eis".
Ein Eisschnellläufer mit einer Masse von 75 kg übt eine Gewichtskraft von 75 kg · 9,81 m/s² = 736 N aus.
- Plane Kufe: Verteilt auf 6 cm² entspricht das einem Druck von 736 N / 6 cm² = 123 N/cm² = 12,3 bar, sofern
  - die Eisfläche absolut eben ist und die plane Kufe mit ihrer vollständigen Fläche auf der Eisfläche aufliegt. Dies ist in der Realität allerdings selten der Fall.
  - Dabei würde der Schmelzpunkt um 12,3 × 0,0077 K sinken, also lediglich um 0,09 K.
- Hohlschliffkufe: Verteilt auf die Kanten der hohlgeschliffenen Kufe mit einer Auflagefläche von nur einem 1/100 der obigen Rechteckfläche wird bereits ein Druck von 1230 bar erzeugt. Ein Druck von 1230 bar würde den Schmelzpunkt auf ca. -10 °C verschieben. Daher liegt die Eistempertur von Kunsteisbahnen zwischen -12 °C bis -7 °C.

Schon bei −1 °C wäre dann theoretisch kein Eislauf mit einer rechteckigen planen Kufe möglich, wenn nur die Druckaufschmelzung als Erklärung herangezogen würde. Die Druckaufschmelzung kann also nicht nur für den Mechanismus des Schlittschuhlaufens herangezogen werden. Zu bedenken ist dabei auch, dass alle anderen Gleitwerkzeuge (Skier, Schlitten etc.) noch größere Flächen haben und noch geringeren Druck ausüben. Zusätzlich ist unterhalb von ca. −22 °C (Tripelpunkt von Wasser, Eis I_h und Eis III) das Eislaufen oder Schifahren schwieriger (griffiger), weil unterhalb dieser Temperatur kein flüssiges Wasser mehr existiert.

Zur Erinnerung die physikalischen Einheitendimensionen:

1 Newton (Einheit) = 1 kg·m/s²
eine Masse von 1 kg übt auf der Erde auf Meereshöhe eine Gewichtskraft von 9,81 kg·m/s² ≈ 10 Newton aus.
10 N/cm² = 1 bar

Einzelnachweise

Martin Chaplin (London South Bank University): Explanation of the Density Anomalies of Water: D2 Water expands on freezing (englisch), abgerufen am 28. Dezember 2018
Jürgen Vollmer, Ulrich Vetter: Schlittschuhlaufen: Warum ist Eis so glatt? In: Welt der Physik, 22. Februar 2008, abgerufen am 28. Dezember 2018.
Patrick Kharadi: Der Eiskunstlauf-Schliff. Abgerufen am 2. Februar 2019 (deutsch).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Martin Chaplin (London South Bank University): Explanation of the Density Anomalies of Water: D2 Water expands on freezing (englisch), abgerufen am 28. Dezember 2018

[2] Jürgen Vollmer, Ulrich Vetter: Schlittschuhlaufen: Warum ist Eis so glatt? In: Welt der Physik, 22. Februar 2008, abgerufen am 28. Dezember 2018.

[3] Patrick Kharadi: Der Eiskunstlauf-Schliff. Abgerufen am 2. Februar 2019 (deutsch).