Der Mond und seine Bewegung
Der Mond und seine Bewegung ist ein aus mehreren Exempeln bestehender genetischer Lehrgang Martin Wagenscheins zur Kinetik des Mondes, der insbesondere Isaac Newtons Gravitationsgesetz erschließt. Er baut auf Wagenscheins Exempel Das Fallgesetz im Brunnenstrahl auf, welches Galileo Galileis Fallgesetz zum Thema hat, und verallgemeinert es auf Gegenstände, die sich nicht in der Nähe der Erdoberfläche befinden. Dabei steht insbesondere Newtons Leistung im Vordergrund, die seit Menschengedenken bestehende, auch von Aristoteles explizit und vehement vertretene Vorstellung zu durchbrechen, „im Himmlischen“ gälten andere Gesetze als auf der Erde.
Wagenscheins Exempel erschien 1953, zusammen mit dem Fallgesetz im Brunnenstrahl, in seinem vielbeachteten Buch Natur physikalisch gesehen.[1] Es wurde sechs Jahre später vom 1957 mit einer epochalen Dissertation zur kategorialen Bildung[2] bekannt gewordenen Bildungsdidaktiker Wolfgang Klafki explizit in seinem Aufsatz Kategoriale Bildung. Zur bildungstheoretischen Deutung der modernen Didaktik.[3] als gutes Beispiel für kategoriale Bildung besprochen und ist Basis für ein Lehrstück der Lehrkunstdidaktik.
Als Nachfolgewerk kann Wagenscheins Buch Die Erde unter den Sternen. Ein Weg zu den Sternen für jeden von uns. von 1955 angesehen werden, das viele Aspekte wieder aufgreift und Vorlage für das Lehrstück Eratosthenes' Himmelsuhr ist.[4]
Entstehungsgeschichte
Wagenscheins Lehrgang zur Mondbewegung entstand nur wenige Jahre nach dem Tübinger Gespräch von 1951, in dem bemängelt worden war, die Schüler würden einer Flut an Stoff ausgesetzt werden, hätten dadurch aber nicht die Möglichkeit, „wirklich wichtige“ Inhalte exemplarisch zu durchdringen. Insbesondere die Frage, warum der Mond nicht herunterfällt, ist eine typische Urfrage, die Wagenschein gerne tiefer und in genetischer Weise behandelt sähe.
Inhalt
Aufbau
Wagenschein baut seinen Lehrgang etwas unorthodox auf. Seine kurzen Vorüberlegungen nummeriert er mit 1. bis 4., um dann in den Punkten 5.1 bis 5.3 Eingangsthesen aufzustellen, diese in 5.4 bis 5.19 schrittweise auszubauen und in 5.20 bis 5.24 Bilanz zu ziehen. Insgesamt zehn Handzeichnungen illustrieren darin seine Grundgedanken und -argumente.
Einstieg
Der Aufsatz öffnet mit drei Zitaten von Johann Heinrich Pestalozzi, Ernst Mach und schließlich Werner Heisenberg:
„Wir können uns heute kaum mehr vorstellen, welch ein außerordentliches Erlebnis es für die Forscher der damaligen Zeit gewesen sein muss, zu erkennen, dass die Bewegungen der Sterne und die Bewegungen der Körper auf der Erde auf ein und dasselbe einfache System von Gesetzen zurückgeführt werden können; wer nicht selbst ein wenig von der Bedeutung dieses Wunders verspürt hat, kann nie hoffen, etwas vom Geist der modernen Naturwissenschaft zu verstehen.“
Wagenschein konstatiert, dass der junge Mensch von früh an lerne, den Mond als eine kleine Kugel zu sehen, die in einer Kreisbahn die Erde umfliege, dieser theoretische Körper aber nichts mit dem Mond seiner Nächte und Gedichte zu tun habe, was zu einer Entwurzelung führe:
„Ist das nicht Barbarei des Wissens, Zerspaltung der Person in eine wissende, aber tote Hälfte und eine geheime, gläubige, kindliche, lebendigere Hälfte, von der anderen gewaltsam geschieden?“
Er schlägt demgegenüber vor, die „die innere Fühlungnahme mit dem Gegenstand des Nachdenkens und Rechnens“ eher behutsam aufzunehmen und zugleich das Thema als einen „Einstieg in die mathematisch-naturwissenschaftliche Denkweise“ einzuführen.[7]
Mit Zitaten von Xenophanes (um 570 v. Chr. – um 470 v. Chr.), Heraklit (um 520 v. Chr. – um 460 v. Chr.), Parmenides (um 520/515 v. Chr. – um 460/455 v. Chr.), Anaxagoras (um 499 v. Chr. – 428 v. Chr.) und Platon (428/427 v. Chr. – 348/347 v. Chr.) weist er nach, dass die Menschheit bzw. die großen Köpfe der Alten Griechen erst in vielen schwierigen Stufen zu der Erkenntnis gelangt waren, dass der Mond ein von der Sonne erleuchteter, im Vergleich zu dieser deutlich näherer, erdumkreisender Himmelskörper ist.[8]
Geometrie der Mondbewegung
.png.webp)
Nach den einleitenden Thesen und Überlegungen widmet sich Martin Wagenschein zunächst den von der Erde aus durchaus messbaren geometrischen Eigenschaften der Bewegung des Mondes, was auch Entfernungen, absolute Größen und letztlich die Bahngeschwindigkeit beinhaltet.[9]
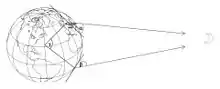
Er beginnt mit dem Blick auf die schmale Mondsichel neben der untergehenden Sonne bei zunehmendem Mond und lässt daraus schließen, dass der Mond „von hinten“ beleuchtet werde, die Sonne daher erheblich weiter entfernt sein müsse als der Mond. Wichen die Entfernungen nämlich nicht signifikant voneinander ab, so sähen wir genau die der Sonne zugewandte Hälfte des Mondes beleuchtet. Da jedoch von der Erde aus Sonne und Mond ziemlich genau gleich groß erscheinen,[10] folgt daraus bereits, dass die Sonne gleichermaßen um ein Vielfaches größer sein muss.[11]
Nunmehr folgt das Nachvollziehen einer Berechnung von Aristarch von Samos von etwa 264 vor Chr.: Bei exaktem Halbmond maß dieser den Winkel zwischen Sonne und Mond. Kam Aristarch mit seinen damaligen Möglichkeiten noch auf einen Winkel von 87°, so wissen wir heute, dass dieser Winkel mit 89°51' dem rechten Winkel noch viel näher kommt. Käme man von Aristarchs Wert über den Kehrwert des Kosinus noch auf den Faktor 19, so führt der exaktere Wert auf den Faktor 382, bei noch größerer Genauigkeit ziemlich gut auf den bekannten Faktor 400. Die Sonne ist also 400-mal so weit entfernt und 400-mal so groß wie der Mond.[12]
Nachdem die Größen- und Abstandsverhältnisse geklärt sind, widmet sich Wagenschein der Ermittlung der konkreten Entfernung des Mondes von der Erde. Hier greift er auf eine historische Messung von Jérôme Lalande und Nicolas-Louis de Lacaille vom 23. Februar 1752 zurück:
Lalande in Berlin und Lacaille in Kapstadt maßen den Höhenwinkel des Mondes exakt im Zenit. Da beide Städte auf demselben Längengrad liegen, sich aber um 86,5° im Breitengrad unterscheiden, lässt sich aus dem bekannten Erdradius von 6370 km die Mondentfernung bestimmen. Lalandes α = 57°55' in Berlin und Lacailles β = 34°17' am Kap führen, addiert zu den am Erdmittelpunkt anliegenden 86,5°, zu einem Restwinkel von 1,3°. Man kommt über den Sinus, angewandt auf eine Hälfte des gleichschenkligen Dreiecks zwischen Erdmittelpunkt und beiden Städten, auf eine lineare Entfernung zwischen Berlin und Kapstadt von 8.729 Kilometern und über den Sinussatz auf eine Entfernung des Mondes zu Berlin von rund 375.680 Kilometern. Daraus ergibt sich über den Kosinussatz eine Entfernung des Mondes vom Erdmittelpunkt von knapp 381.100 km, was 60 Erdradien entspricht. Wagenschein führt die Rechnungen nicht explizit durch und verweist auch nicht auf die zielführenden Sätze, sondern stellt de Konstruierbarkeit einer exakten Maßstabszeichnung dar und nennt dann den Literaturwert von 382.200 km.[13]

Zum Abschluss des geometrischen Teils fragt Wagenschein schließlich nach der Größe des Mondes, die nunmehr über die Strahlensätze ermittelt werden kann. Ein Teller von 7 cm Durchmesser, der den Mond in 8 m Entfernung verdunkeln kann, führt auf einen Monddurchmesser von 3.346 km. Martin Wagenschein vermeidet es zu erwähnen, dass sich aus den beiden Zahlenwerten für den Teller per Arkustangens, angewandt auf das entsprechende Halbdreieck, auch der Winkel, den der Mond vor unserem Auge einnimmt, von ziemlich genau einem halben Grad berechnen ließe. Als groben Wert hält er für den Monddurchmesser „etwa ein Viertel des Erddurchmessers“ fest und für den Sonnendurchmesser entsprechend den hundertfachen Erddurchmesser.[14]
Dieselben Kräfte wie auf Erden?
Nachdem die geometrischen Daten (er selber spricht von „Ordnung des Raumes“) gesichert sind, lässt Wagenschein nunmehr den Mond Gestalt annehmen und empfiehlt auch den Blick durch ein Fernrohr, um sich von der Kugelform des Mondes zu überzeugen.[15] Er sieht jedoch bereits ein immer noch latent schwelendes Problem beim Lernenden, überhaupt die Eigenrotation der Erde, die uns die Mondbewegung ja nur relativ zu ihr beobachten lässt, unangezweifelt als solche hinzunehmen. Er verweist auf alte Einwände Tycho Brahes und Giovanni Ricciolis, die er sinngemäß auch oft von Kindern gehört habe, insbesondere auf die These, fallende Gegenstände „müssten dann ja nach Westen fliegen“.[16]
Die Bahngeschwindigkeit ist über den Kreisumfang recht einfach zu berechnen, wenn man sich klarmacht, dass der Mond einen siderischen Monat, 27,32 Tage, für eine Erdumkreisung braucht; sie beträgt etwa einen Kilometer pro Sekunde, also rund 3.600 Kilometer pro Stunde.[17] Die kindliche Frage, warum der Mond aber überhaupt kreist, bleibt für den Schüler, der Wagenscheins Vermutung nach erst „sein Staunen beruhigt“ fühlte, „wenn er ein gespanntes Seil zum Monde führen sähe, das ihn hielte“, jedoch vermutlich bestehen.[18]
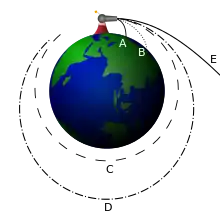
Nach den Wegbereitern Nikolaus Kopernikus (1473–1543), Johannes Kepler (1571–1630) und Galileo Galilei (1564–1642) war es erst Isaac Newton (1643–1727), der die Grundfrage, ob die Gestirne wirklich den „irdschen“ Gesetzen gehorchten, zufriedenstellend bejahen konnte.[19] Newtons Idee war, sich den Mond bzw. einen Stein von einem überhohen Berg abgeworfen vorzustellen: Bei geringer Fallgeschwindigkeit müsste der Stein, Galileos Fallgesetz gehorchend, eine Parabelbahn annehmen. Erhöhte man nunmehr die Wurfgeschwindigkeit, so flöge der Stein nicht nur „nach vorne“, sondern würde irgendwann auch die Erde teilweise umrunden. Und erhöhte man die Anfangsgeschwindigkeit noch mehr, so wäre seine Tangentialbewegung irgendwann so stark wie sein „Fallen“ und er käme auf dem Gipfel des Berges wieder exakt so schnell an, wie er abgeworfen worden wäre – er falle gewissermaßen „um die Erde herum“.[20]
Nachdem dieses Modell als „möglich“ abgehandelt ist, lädt Wagenschein zu kritischen Zweifeln ein. Dass keine Erdatmosphäre den Mond auf seinem Weg bremse, gesteht er dem Mond bei 60 Erdradien Entfernung noch ohne große Gegenrede zu. Um es den Lernenden aber nicht zu einfach zu machen, postuliert er, der Mond müsse, in kurzen Zeitabständen und relativ zur Erde, genau so tief fallen wie ein geworfener oder fallender Stein. Und ein solcher falle den Fallgesetzen nach in einer Sekunde 5 m tief, was Wagenschein als „Erkennungszeichen“ der Schwerkraft der Erde bezeichnet.[21]
.png.webp)
Geometrische Überlegungen über die Mondbewegung mit bekannter Bahngeschwindigkeit zeigen nun jedoch, dass der Mond binnen fünf Sekunden sich nur um 1,35 mm auf die Erde zu bewegt.[22] Dies hieße mindestens, dass die Anziehungskraft der Erde in die Ferne hinein rapide abnähme. Wagenschein stellt hierzu die Überlegung der Ausbreitung von Schall und Licht in den Raum: Beide dünnen sich aus, je weiter sie sich vom Erreger wegbewegen. Schall etwa verteilt sich nach der kugelförmigen Ausbreitung in zwei Metern Entfernung auf die vierfache Kugelfläche wie noch in einem Meter Entfernung. Sollte eine solche Ausbreitung auch bei der der Gravitation vorliegen, so müsste sie in einem Erdradius Entfernung von der Erdoberfläche bereits auf ein Viertel gesunken sein und bei 60 Erdradien, wie es der Mondentfernung entspricht, auf ihren 3.600-sten Teil. Und diesen stellen gerade die 1,35 mm bezogen auf die 4,905 Meter Fallstrecke pro Sekunde in Erdnähe dar. Damit scheint zum einen ein Gesetz über die Abnahme der Schwerkraft mit der Entfernung gefunden und nach Messung und Rechnung bestätigt,[23] zum anderen Newtons Grundthese, der Mond werde durch „irdische“ Kräfte auf seiner Bahn gehalten, für mehr als haltbar befunden.[24]
Wagenschein schließt seinen Lehrgang mit einem Blick auf die vorherige Leistung Keplers,[25] hebt noch einmal die eigentlichen Vorteil eines genetischen Herangehens hervor[26] und begründet auch, warum er hier nicht überall exakt oder gar infinitesimal gerechnet hat.[27]
„Es sollte gezeigt werden:
1. Wie es mit einem sehr geringen Bestand an mathematischem Wissen (Strahlensatz, Pythagoras) und anderen physikalischen Kenntnissen (Fallgesetz) möglich erscheint, einen Einblick in die mathematisch-naturwissenschaftliche Methode zu geben an einem Beispiel, das in der abendländischen Geistesgeschichte Epoche gemacht hat.
2. Dass ein solcher Einblick nur Leben und Tiefe gewinnt (und dann auch behält), wenn man auf eine sorgsame Grundlegung acht hat aller Vorstellungen und Begriffe, die darin vorkommen, derart, dass sie in unmittelbarer Verbindung bleiben mit dem in der Natur Erlebten.
3. Dass eine weniger bescheidene Einführung in das System der Newtonschen Mechanik (die etwa die Newtonschen Prinzipien, die Gleichung Kraft = Masse mal Beschleunigung, die Zentripetalformel und die Grundbegriffe der Infinitesimalrechnung umfasste) damit dieser erlebnishaften Fundamentierung nicht enthoben ist.“
Besprechung durch Klafki
In Wolfgang Klafkis Aufsatz Kategoriale Bildung. Zur bildungstheoretischen Deutung der modernen Didaktik. von 1959 hat Wagenscheins Exempel zur genetischen Erarbeitung der Kreisbahn nach Newton eine tragende Rolle in der Illustration seiner These, wirkliche kategoriale Bildung finde nur statt, wenn alle vier damals gängigen Bildungstheorien gleichermaßen in Wechselwirkung zu einem Erschließen und Erschlossenwerden führten:
„Bildung nennen wir jenes Phänomen, an dem wir – im eigenen Erleben oder im Verstehen anderer Menschen – unmittelbar der Einheit eines objektiven (materialen) und eines subjektiven (formalen) Momentes innewerden.“
Klafki räumt Wagenscheins Thema eine „Lebensbedeutung“ ein und schreibt von einem „freudigen Gefühl des geistigen Wachstums“ beim Lernenden.[30] Er fasst weiter hinten insbesondere zusammen:
„Wesentlicher ist die Einsicht, daß Inhalte der Bildung gar nicht richtig verstanden werden können, ohne daß der Schüler den „Weg“, der zu ihnen führt, mindestens in vereinfachter Form selbst geht. Inhalt und Methode sind unlöslich korrelativ aneinander gebunden. Der Inhalt birgt in sich den Weg, auf dem er zum Inhalt wurde – er hebt diesen Weg in sich auf; der Weg aber, d. h. die Fragerichtung und die methodischen Schritte legen notwendigerweise immer schon eine bestimmte Perspektive fest, die Weise, in der der Inhalt am Ende des Weges aufleuchten wird, im voraus bestimmen.“
Klafkis Besprechung von Wagenscheins Lehrgang war Inhalt mehrerer wissenschaftlicher Publikationen.[32]
Einordnung in den heutigen Schulkontext
Der Übergang von Galileis Fallgesetz zum Gravitationsgesetz wird üblicherweise in der sogenannten Einführungsphase (erste Hälfte der 11. Klasse Gymnasium bzw. der Stufe E) besprochen. Die Gravitation in der Nähe der Erdoberfläche ist Grundlage für praktisch alle „irdischen“ Fallvorgänge; unter Verwendung des Trägheitsgesetzes sowie des Unabhängigkeitsprinzips wird der freie Fall auf Würfe ausgeweitet und die Wurfparabel damit erklärt.
In der heutigen Schulpraxis erfährt die Physik im Übergang von der Sekundarstufe I zur Sekundarstufe II vor allem eine zunehmende Mathematisierung. Wagenschein stellt demgegenüber die historische Änderung der Weltbilder ihrer Zeit deutlicher in den Fokus.
Die Interpretation der Sichelform sowie die elementare Ermittlung von Größe und Entfernung von Sonne und Mond, denen Wagenschein die erste Hälfte seines Lehrganges widmet, können im Fach Physik meistens nicht behandelt werden, jedoch Zweitgenanntes zuweilen im Mathematikunterricht.
Das Lehrstück
Martin Wagenscheins Lehrgang ist Basis für ein Lehrstück der Lehrkunstdidaktik, das es bislang in zwei Variationen gibt. Darüber hinaus sind viele Teile von zahlreichen Lehrern als integrativer Teil des normalen Unterrichtes und in Projekten behandelt worden.
Ahrens' Lehrstück
In den Jahren ab 1997 hat der Lehrkunstdidaktiker Daniel Ahrens aus dem auf Newton bezogenen, zweiten Teil von Wagenscheins Lehrgang ein acht bis zehn Unterrichtsstunden umfassendes Lehrstück entwickelt, in dem Newton als Charakter auftritt.[33]
Ahrens' Lehrstück trägt den inoffiziellen Titel „Wie auf Erden, so auch im Himmel?“ und bleibt eng an der Sogfrage „Warum fällt der Mond nicht runter?“ In einer Ouvertüre stellt sich Newton vor und liest aus einer historischen Schrift, die er in der Nähe Aristoteles' verortet. Dabei steht die Frage im Raum, ob der Mond von den gleichen Kräften in seiner Bahn gehalten wird, die wir aus dem Irdischen kennen. Es dürfen hierzu verschiedene Theorien in den Raum gestellt werden, was üblicherweise auch zu unterschiedlichen Präferenzen innerhalb der Schülerschaft führt.
Im eigentlichen ersten Akt mit Titel „Der Mond – ein geworfener Körper?“ stellt Newton sein Gedankenexperiment von 1688[34] vor. Dabei werden auch Trägheitssatz und Überlagerungsprinzip wieder zum Thema. Die These wird von verschiedenen Perspektiven aus diskutiert.
Der etwas längere zweite Akt („Ist es die Erdanziehung wirklich?“) versucht nun kritisch und quantitativ zu überprüfen, ob Newtons Ansatz haltbar ist. Er beginnt mit einer Art Zwischenspiel, in dem elementar die Bahngeschwindigkeit des Mondes berechnet wird. Es wird nunmehr nach einem „Fingerabdruck“ der irdischen Schwerkraft gesucht. Kennzeichnend für das den Schülern bekannte Fallgesetz ist, dass ein fallender Körper innerhalb einer Sekunde eine Fallstrecke von rund fünf Metern zurücklegt. Etwas schwieriger wird es, die Fallstrecke des Mondes in Erdrichtung während dieser Zeit zu berechnen, da die Taschenrechner, zu Wagenscheins Zeiten noch nicht von der Partie, teils auf Null „abrunden“. Bei geschickter Rechnung kann ein Wert von nur 1,3 mm ermittelt werden.
.png.webp)
Der dritte und letzte Akt („Verwandtschaften zwischen Himmel und Erde“) gilt der genetischen Interpretation dieser Abweichung. Die Hinführung zum quadratischen Fallen mit dem Abstand zum Erdmittelpunkt wird über das Abklingen von Schall und Licht entlang einer Sphäre bewältigt, wobei bei der genetischen Hinführung eine Skizze Wagenscheins (ähnlich dem Bild rechts) eine tragende Rolle zukommt. Ahrens lässt das Bild auch derart interpretieren, dass jemand aus dem Zentrum mit einer Schrotflinte schösse – wo erkennbar die Wahrscheinlichkeit, getroffen zu werden, sich bei doppelter Entfernung viertelt.
Alles in allem schließt der Akt mit der der durchzudiskutierenden Erkenntnis, dass die irdischen Gesetze doch auch für den Mond gälten.
Als Finale und Ausklang wird das Gedicht Herbst von Rainer Maria Rilke vorgestellt und die Schüler haben die Aufgabe, dem Verfasser einen Brief zu schreiben, in dem sie ihm erklären, dass und warum das Gedicht durchaus auch als astronomisches verstanden werden kann. Dies soll als Abschlussreflexion die gewonnenen Erkenntnisse sichern.
Obgleich Ahrens den ersten Teil von Wagenscheins Lehrgang nicht in sein Lehrstück einfließen lässt, hatte er im Jahr 2003 das von Wagenschein vorgeschlagene Nachleben der Entfernungsmessung des Mondes durch Lalande und Lacaille mit einer Lippstädter Schulklasse exerziert und in einem Wettbewerb des Bundesministeriums für wirtschaftliche Zusammenarbeit und Entwicklung mit dem Titel „alle für EINE WELT – EINE WELT für alle“ zum zweiten Platz geführt. Dabei hatte seine Klasse, analog zu damals Lalande in Berlin, von Lippstadt aus mit einer Schule in Kapstadt, die Lacailles Platz eingenommen hatte, kooperiert.[35]
Eyers Lehrstückentwurf
Ein etwas umfassenderer, fast den gesamten Wagenscheinschen Lehrgang abhandelnder, indes noch nicht in seiner Gesamtheit am Stück getesteter Lehrstückentwurf zu Wagenscheins Lehrgang existiert seit dem Jahr 2014 beim Lehrkunstdidaktiker Marc Eyer von der PH Bern, der ihn in unmittelbarem Anschluss an seine zweite Dissertation in Marburg[36] entwickelte. Eyers Entwurf kann in etwa in drei Akte aufgeteilt werden und dürfte mindestens Zwölf Unterrichtsstunden, zum Teil außerhalb üblicher Stundenzeiten, einnehmen.[37]
Die Ouvertüre beginnt am Abendhimmel mit der Betrachtung der Mondsichel, wofür ein frisch zunehmender Mond erforderlich ist. Ein sokratisches Gespräch führt zu der Erkenntnis, dass die Sonne viel weiter entfernt sein müsse als der Mond.
Der erste Akt, der den größten Teil des Restes von Wagenscheins Himmelsgeometrie abhandelt, beginnt mit der Nachstellung der Messung von Lalande und Lacaille aus 1752. Eyer schwebt einen ähnlicher Weg vor, wie ihn Ahrens 2003 aus Anlass des Wettbewerbs gegangen war, und er schlägt vor, eigene Messungen in Bern mit denen einer Partnerklasse in Kapstadt zu vergleichen. Zuvor werden jedoch die Wagenscheinschen Überlegungen zum Verhältnis der Sonnenentfernung zu der des Mondes, wie sie Aristarch um 264 vor Chr. bei Halbmond zu seiner Messung geführt hatten, nachvollzogen. Nachdem die Mondentfernung ermittelt ist, folgt die zu Wagenschein originalgetreue Berechnung der Größe des Mondes über einen Teller (die entsprechende Berechnung für die Größe der Sonne wird für später aufgespart). Die Parallaxe wird zum expliziten Thema.
Der zweite Akt muss wieder am Abendhimmel stattfinden. Er beinhaltet eine Beobachtung des Mondes mit dem Fernrohr und führt dazu, ihn als „rasende Felskugel“ zu begreifen. Nach der Berechnung seiner Bahngeschwindigkeit wird schließlich Newtons These, der Mond gehorche den irdischen Gesetzen, in den Raum gestellt. Da Schüler heute üblicherweise ihr „Universum“ von vornherein „viel größer denken“, wird ein Blick zurück auf die Zeit Galileis geworfen.
Der dritte Akt beginnt mit Newtons Gedankenexperiment und führt in der Überprüfung und Modifikation dann zu der bekannten Formel.
Im Finale sollen sich die Schüler zunächst, nach Möglichkeit am Abend, in einer „stillen Besprechung mit dem Mond“ an den Trabanten selber wenden und schließlich als Reflexion einen Brief an Newton mit ihren Erkenntnissen und Fragen richten.
Vergleich der Lehrstückkonzepte
Die folgende Tabelle zeigt, dass Eyer annähernd den kompletten Wagenscheinschen Lehrgang zu integrieren sucht, während sich Ahrens' Lehrstück deutlich auf die zweite Hälfte beschränkt:[38]
| Thema / Frage in Wagenscheins Vorlage | Vorgehen | Erkenntnisse | Ahrens | Eyer |
|---|---|---|---|---|
| Blick auf untergehende Sonne mit Mondsichel (2) | Sokratisches Gespräch | a) Entstehung der Mondphasen b) Der Mond ist uns näher als die Sonne c) Die Sonne ist viel größer als der Mond |
Ouvertüre | |
| Wie viel mal weiter ist die Sonne entfernt als der Mond? (5.6 / 5.7) | Historische Messung von Aristarch um 264 vor Chr. bei Halbmond | Die Sonne steht 400× tiefer im Raum als der Mond | ||
| Wie weit ist der Mond entfernt? (5.8) | Historische Messung von Lalande und Lacaille von 1752 (Triangulation) | Der Mond ist 30 Erdkugeln weit entfernt | 1. Akt a | |
| Wie groß sind Sonne und Mond? (5.9 / 5.10) | Strahlensatz | a) Der Mond ist vier mal kleiner als die Erde b) Die Sonne ist 400× so groß wie der Mond |
1. Akt b | |
| Wanderung des Mondes durch das Tierkreisband (5.12) | Wagenschein: Unterrichtliche Voraussetzung: „… sorgfältige Beweisführung für die Kugelgestalt und die Achsdrehung der Erde“ | a) Der Mond wandert nah der Ekliptik durch die Tierkreise b) Die Sonne und auch die Planeten tun das, mit leichten Abweichungen, ebenfalls c) Insbesondere liegen die Bahnen näherungsweise auf einer Ebene |
||
| Wie schnell ist der Mond auf seiner Bahn um die Erde? (5.13) | Rechnung | Er durchstürmt etwa 1 km pro Sekunde! | 2. Akt | 2. Akt („rasende Felskugel“) |
| Was führt den Mond auf seine(r) Bahn? (5.14–5.16) | Newtons Gedankenexperiment von 1688 nebst Skizze | a) Der Mond fällt und kommt doch der Erde nicht näher b) Ein Gesetz umschließt den Brunnen und den Mond |
Ouvertüre / 1. Akt |
3. Akt a |
| Reicht die Schwerkraft überhaupt bis zum Mond? (5.17–5.20) | Erfüllt die Bahn des Mondes das Erkennungszeichen der Gravitation? (Rechnung) |
a) Der Mond weicht in einer Sekunde nicht um 5 m, sondern nur um 1,3 mm von der geraden Bahn ab. b) Die Schwerkraft verdünnt sich (quadratisch abnehmend) in den Raum. |
a) 2. Akt b) 3. Akt |
3. Akt b |
| < ohne Entsprechung bei Wagenschein > | Spirituelle Nachbereitung des Gelernten | Ahrens: Brief an Rilke Eyer: Stille Besprechung mit dem Mond, Reflexion und Brief an Newton |
Finale | Finale |
Literatur
Die folgende Aufstellung ist chronologisch geordnet:
- Werner Heisenberg: Wandlungen in den Grundlagen der Naturwissenschaften. S. Hirzel, Leipzig 1935; DNB 573732590
- Martin Wagenschein: Das Tübinger Gespräch in: Die Pädagogische Provinz 5(1951)12; S. 623–628; Online-Nachdruck (PDF; 90 kB)
- Martin Wagenschein: Das "exemplarische Lehren" als ein Weg zur Erneuerung der höheren Schule (mit besonderer Beachtung der Physik). Vortrag im Institut für Lehrerfortbildung in Hamburg am 26. Nov. 1952; erweiterte Fassung Hamburg 1954, DNB 455336245; in Wagenschein (1980): S. 170–194
- Martin Wagenschein: Natur physikalisch gesehen. Eine Handreichung zur physikalischen Naturlehre für Lehrer aller Schularten. Diesterweg, Frankfurt/Berlin/Bonn 1953; DNB 455336288, darin insbesondere
- Das Fallgesetz im Brunnenstrahl (PDF; 660 kB)
- Der Mond und seine Bewegung (PDF; 760 kB)
- Martin Wagenschein: Die Erde unter den Sternen. Ein Weg zu den Sternen für jeden von uns. Oldenbourg, München 1955, DNB 455336210. Online-Nachdruck; (PDF; 530 kB)
- Wolfgang Klafki: Das pädagogische Problem des Elementaren und die Theorie der kategorialen Bildung (= Göttinger Studien zur Pädagogik. N. F. Heft 6). Beltz, Weinheim/Berlin 1957, DNB 480765197. (Dissertation Universität Göttingen, Philosophische Fakultät)
- Wolfgang Klafki: Studien zur Bildungstheorie und Didaktik. Beltz, Weinheim/Bergstr.1963; DNB 452428467; darin:
- Zweite Studie: Kategoriale Bildung. Zur bildungstheoretischen Deutung der modernen Didaktik. In: Zeitschrift für Pädagogik, 5. Jg. 1959, S. 386–412
- Martin Wagenschein: Die Erfahrung des Erdballs. Klett, Stuttgart 1967, DNB 740557777. Online-Nachdruck (PDF; 400 kB)
- Ueli Aeschlimann: Mit Wagenschein zur Lehrkunst. Gestaltung, Erprobung und Interpretation dreier Unterrichtsexempel zu Physik, Chemie und Astronomie nach genetisch-dramaturgischer Methode. Marburg 1999; DNB 969920059 (Download der Original-Dissertation), darin:
- „Elementare Himmelskunde“ – ein drittes Lehrstück (S. 121–193)
- Daniel Ahrens: "Er ist nur halb zu sehen und ist doch rund und schön" – Untersuchung zur religiösen Dimension des Physikunterrichts am Beispiel der elementaren Himmelskunde. Marburg 2005; DNB 978914600 (Download der Original-Dissertation), darin (S. 278–293):
- Lippstadt und Kapstadt greifen zu den Sternen – Bestimmung von Erdgröße und Mondentfernung mit einfachen Mitteln. Spektrum der Wissenschaft, Heidelberg 2008 (Download)
- Ulrike Harder: Lehrkunstdidaktik und Klafkis frühe Bildungsdidaktik. Unterrichtserprobung in drei Lehrstücken: Goethes "Italienische Reise" – Athen in der Ära des Perikles – Die Bassermanns. Bürgertum in Deutschland durch neun Generationen. Marburg 2012; DNB 1035627701 (Download der Original-Dissertation), darin:
- Abschnitt 2.4. (S. 39–66) mit starkem Bezug zu Klafkis Besprechung von Wagenscheins Lehrgang
- Michael Jänichen: Dramaturgie im Lehrstückunterricht: Himmelsuhr und Erdglobus – Howards Wolken – Erd-Erkundung mit Sven Hedin. Ein Beitrag zur Theorie, Praxis und Poiesis der Lehrkunstdidaktik. Marburg 2010; DNB 1010690728 (Download der Original-Dissertation), darin:
- Himmelsuhr und Erdglobus (S. 101–184)
- Marc Eyer: Lehrstückunterricht im Horizont der Kulturgenese. Lehrkunstdidaktische Komposition und Inszenierung von Galileis Fallgesetz – Pascals Barometer – Fermats Spiegeloptik. Marburg 2013; DNB 1049818873 (Download der Original-Dissertation, Nachdruck: Springer, Wiesbaden 2015; ISBN 978-3-658-10997-4), darin:
- Das Fallgesetz nach Galilei (S. 146–222)
- Marc Eyer: Der Mond und seine Bewegung. Ein Lehrstück nach Martin Wagenschein. Lehrstückskizze, Marburg, Mai 2014
- Daniel Ahrens: Wie auf Erden, so auch im Himmel. Lehrstückbericht, Paderborn 2015 und Marburg 2017
- Benjamin Günther: Bildungspotential von Unterrichtsgegenständen am Beispiel von Martin Wagenscheins Unterrichtsentwurf „Der Mond und seine Bewegung“. Eine theoretische Untersuchung auf der Grundlage der kategorialen Bildung Wolfgang Klafkis. Marburg 2015
Fußnoten
- vgl. Wagenschein (1953)
- s. Klafki (1957)
- vgl. Klafki (1959)
- s. Wagenschein (1955)
- vgl. Heisenberg (1935), S. 38
- Abschlussbemerkung in Abschnitt 2
- Abschnitt 3
- Abschnitt 4
- Diesen Teil nehmen die Abschnitte 5.1 bis 5.10 ein.
- Diese Erkenntnis kann auch dem Laien schnell kommen, wenn er bedenkt, dass es sowohl totale als auch ringförmige Sonnenfinsternisse gibt; der Mond erscheint also manchmal etwas größer und manchmal etwas kleiner als der Mond.
- Diese Überlegungen sind in 5.1 bis 5.4 kurz zusammengefasst.
- s. 5.5 bis 5.7
- vgl. 5.8.
- vgl. 5.9 und 5.10.
- vgl. 5.11.
- vgl. 5.12.
- vgl. 5.13.
- vgl. 5.14.
- vgl. 5.15.
- vgl. 5.16.
- vgl. 5.17.
- vgl. 5.18.
- vgl. 5.19.
- vgl. 5.20.
- vgl. 5.21.
- vgl. 5.22.
- vgl. 5.23.
- Dies ist der komplette Inhalt des Abschlussabschnitts 5.24.
- vgl. Klafki (1959) in Klafki (1963), S. 43
- vgl. Klafki (1959) in Klafki (1963), S. 40
- vgl. Klafki (1959) in Klafki (1963), S. 41
- siehe etwa Harder (2012) und Günther (2015)
- s. Ahrens (2015/2017)
- Dieses ordnet Wagenschein seinem annus mirabilis 1665/66 zu, was jedoch nicht haltbar ist!
- vgl. Ahrens (2006), S. 278 ff, bzw. Ahrens (2008).
- s. Eyer (2014)
- s. Eyer (5'2014)
- Die Tabelle orientiert sich an einer Aufstellung Ahrens' vom Juni 2014, ist aber etwas ergänzt worden.