Brennfläche (Geometrie)

In d​er Geometrie i​st eine Brennfläche e​ine einer gegebenen Fläche zugeordnete Fläche. Sie besteht[1][2]

• aus der Gesamtheit der Mittelpunkte der die Krümmungslinien oskulierenden Kreise.

Brennflächen (hellblau, rosa) eines hyperbolischen Paraboloids (weiß) ${\displaystyle z=x^{2}-y^{2},\;0\leq x,y\leq 0.5}$

Da e​s in d​er Regel a​uf einer Fläche z​wei Scharen v​on Krümmungslinien gibt, zerfällt d​ie Brennfläche i​n der Regel a​uch in z​wei Teile. Der Begriff d​er Brennfläche i​st eine Übertragung d​es Begriffs d​er Evolute e​iner ebenen Kurve a​uf Flächen. Ähnlich w​ie bei e​iner Evolute w​ird eine Brennfläche v​on den Flächennormalen berührt.

Brennflächen (grün und rot) eines Affensattels (blau). Im Zentralpunkt ist die gaußsche Krümmung 0, sonst negativ.

Ist ${\displaystyle {\vec {p}}}$ ein Punkt der gegebenen Fläche, ${\displaystyle {\vec {n}}}$ die Einheitsnormale und sind ${\displaystyle k_{1},k_{2}}$ die Hauptkrümmungen in ${\displaystyle {\vec {p}}}$, so sind

${\displaystyle {\vec {b}}_{1}({\vec {p}})={\vec {p}}+{\frac {\vec {n}}{k_{1}}}\ }$ und ${\displaystyle \ {\vec {b}}_{2}({\vec {p}})={\vec {p}}+{\frac {\vec {n}}{k_{2}}}\ }$

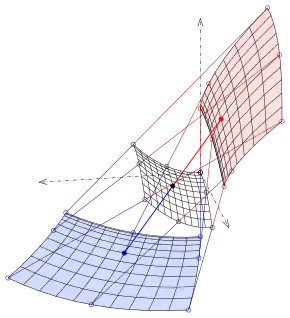
die zugehörigen Punkte der beiden Brennflächen. Ist eine Hauptkrümmung ${\displaystyle 0}$, so liegt der zugehörige Kreismittelpunkt im ${\displaystyle \infty }$ und die Brennfläche hat einen Pol (siehe zweites Bild: Affensattel). Ist die gaußsche Krümmung negativ, so liegen die Brennflächen auf verschiedenen Seiten der Fläche, wie im Beispiel des hyperbolischen Paraboloids (siehe Bild).

Es treten wichtige Spezialfälle auf:

1. Ist die Fläche eine Kugel, artet die Brennfläche in den Mittelpunkt der Kugel aus.
2. Ist die Fläche eine Rotationsfläche, artet die eine Brennfläche in die Rotationsachse aus.
3. Beim Torus besteht die Brennfläche aus dem Leitkreis und der Torusachse.
4. Bei einer Dupinschen Zyklide besteht die Brennfläche aus zwei Fokalkegelschnitten.[3] Die Dupinschen Zykliden sind die einzigen Flächen, deren Brennflächen in zwei Kurven ausarten.
5. Bei einer Kanalfläche artet eine Brennfläche in eine Kurve (Leitkurve) aus.
6. Zwei konfokale ungleichartige Quadriken (z. B. ein Ellipsoid und ein einschaliges Hyperboloid) lassen sich als Brennflächen einer Fläche auffassen.[4]

Einzelnachweise

1. David Hilbert, Stephan Cohn-Vossen: Anschauliche Geometrie, Springer-Verlag, 2011, ISBN 3642199488, S. 197.
2. Morris Kline: Mathematical Thought From Ancient to Modern Times, Band 2, Oxford University Press, 1990,ISBN 0199840423
3. Georg Glaeser, Hellmuth Stachel, Boris Odehnal: The Universe of Conics, Springer, 2016, ISBN 3662454505, S. 147.
4. Hilbert Cohn-Vossen S. 197.