Matched-Z-Transformation

Die Matched-Z-Transformation (englisch matched z-transformation, in deutsch etwa angepasste Z-Transformation und auch als Pol-Nullstellen-Abbildung bezeichnet) ist in der Signalverarbeitung eine Transformation – eine Umwandlungsart in der Mathematik – zwischen der zeitkontinuierlichen und der zeitdiskreten Darstellung von Systemfunktionen. Sie spielt in der digitalen Signalverarbeitung und der Regelungstheorie eine Rolle, da sie eine Umsetzung in der Systembeschreibung zwischen analogen, kontinuierlichen Systemen und digitalen, diskreten Systemen ermöglicht. Transformationen mit ähnlichem Anwendungsbereich sind die bilineare Transformation und die Impulsinvarianzmethode.

Motivation

In der Signalverarbeitung und Regelungstechnik besteht zur Umsetzung im Bereich der digitalen Signalverarbeitung die Anforderung, gegebene zeitkontinuierliche Übertragungsfunktionen G(s) von linearen, zeitinvarianten Systemen in zeitdiskrete Übertragungsfunktionen H[z] mit möglichst identischem Verhalten umzusetzen. Die Übertragungsfunktion G(s) kann beispielsweise ein analoges Filter beschreiben und H[z] stellt eine aus dem analogen Filter abgeleitete, zeitdiskrete Übertragungsfunktion dar, die ein äquivalentes digitales Filter beschreibt.

Die Matched-Z-Transformation bietet gegenüber ähnlichen Verfahren wie der bilinearen Transformation den Vorteil, nichtlineare Verzerrung der Übertragungsfunktionen von G(s) zu H[z] im Übertragungsbereich zu vermeiden. Nachteilig sind die durch dieses Verfahren bedingten Alias-Effekte im zeitdiskreten System.

Beschreibung

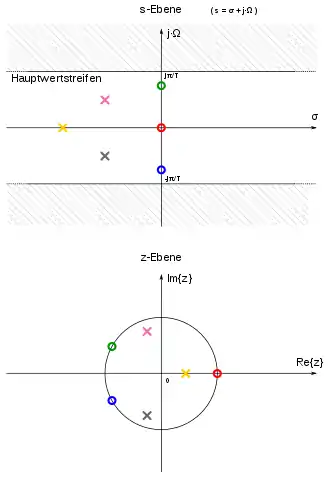
Abbildung dreier Nullstellen (Kreise) und Polstellen (Kreuze) eines Übertragungssystems von der s- in die z-Ebene

Die Beschreibung der Systemfunktionen von zeitkontinuierlichen Systemen erfolgt in der so genannten s-Ebene, in der komplexen Ebene, und ihre Analyse erfolgt mittels der Laplace-Transformation. Bei zeitdiskreten Systemen erfolgt die Darstellung in der so genannten z-Ebene und die Analyse erfolgt mittels der Z-Transformation. Bei linearen, zeitinvarianten Systemen – diese Systeme sind bei der Anwendung der Matched-Z-Transformation vorausgesetzt – lässt sich die Übertragungsfunktion G(s) als rationale Funktion schreiben als:

G(s)=K\cdot {\frac {\prod _{k=1}^{M}(s-n_{k})}{\prod _{k=1}^{N}(s-p_{k})}}.

Mit $M$ Nullstellen $n_{k}$ und $N$ Polstellen $p_{k}$ . Der Faktor $K$ stellt einen Verstärkungsfaktor dar. Bei der Matched-Z-Transformation werden alle Pol- und Nullstellen mit der Beziehung

z=\mathrm {e} ^{sT}

umgesetzt. Der Parameter T stellt das zeitliche Abtastintervall (Periodendauer) des zeitdiskreten Systems dar. Die zeitdiskrete Übertragungsfunktion H[z] wird damit gebildet zu:

H[z]=K'\cdot {\frac {\prod _{k=1}^{M}\left(z-\mathrm {e} ^{n_{k}T}\right)}{\prod _{k=1}^{N}\left(z-\mathrm {e} ^{p_{k}T}\right)}}.

Grafisch ist der Transformationsvorgang in nebenstehender Abbildung qualitativ an einen Übertragungssystem mit drei Null- und drei Polstellen skizziert, der Übergang der einzelnen Punkte ist durch die farbliche Übereinstimmung dargestellt. Liegen im zeitkontinuierlichen System nicht alle Pol- und Nullstellen in der s-Ebene innerhalb des als Hauptwertstreifen bezeichneten nicht schraffierten Bereiches, kommt es im zeitdiskreten System zu Alias-Effekten.

Der Verstärkungsfaktor $K'$ im zeitdiskreten System wird durch Vergleich an charakteristischen Frequenzpunkten gewählt. Beispielsweise bei einem Tiefpassfilter für den Gleichanteil bei der Frequenz 0 s⁻¹. Um gleiche Verzögerungszeiten im zeitdiskreten Filter sicherzustellen, kann es zusätzlich notwendig sein, weitere Pole oder Nullstellen bei $z=0$ hinzuzufügen.[1]

Literatur

Alan V. Oppenheim, Ronald W. Schafer: Zeitdiskrete Signalverarbeitung. 3. Auflage. Oldenbourg, München 1999, ISBN 3-486-24145-1.
Won Young Yang: Signals and Systems with MATLAB. Springer Verlag, 2009, ISBN 978-3-540-92953-6, S. 291 bis 294.

Einzelnachweise

D. Rowell: Signal Processing - Continuous and Discrete - Lecture Note 19 (OpenCourseWare). (PDF; 244 kB) Massachusetts Institute of Technology (MIT), 2008, abgerufen am 4. Februar 2013 (englisch).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[lect19-1] D. Rowell: Signal Processing - Continuous and Discrete - Lecture Note 19 (OpenCourseWare). (PDF; 244 kB) Massachusetts Institute of Technology (MIT), 2008, abgerufen am 4. Februar 2013 (englisch).