Beweisbare Sicherheit

Beweisbare Sicherheit ist ein Konzept in der modernen Kryptologie. In der Geschichte der Kryptographie gibt es viele Beispiele von Systemen, die von ihren Erfindern für sicher gehalten wurden, aber dennoch gebrochen werden konnten. Es ist daher wünschenswert, sich durch einen Beweis auf formalem Weg von der Sicherheit eines Systems zu überzeugen. Dazu muss sowohl das kryptographische System als auch die zu erreichende Sicherheit formalisiert werden.

Perfekte Sicherheit

Claude Shannon definierte 1949 perfekt sichere Verschlüsselungsverfahren und zeigte, unter welchen Bedingungen sie existieren. Ein perfekt sicheres Verschlüsselungsverfahren zeichnet sich dadurch aus, dass ein mit ihm erzeugter Schlüsseltext keinerlei Rückschlüsse auf den korrespondierenden Klartext zulässt. Bei einem solchen Verfahren ist mathematisch bewiesen, dass ein Angreifer, der den Schlüsseltext kennt, abgesehen von der Länge des Klartextes keine weiteren Informationen über diesen gewinnen kann. Er kann den Schlüsseltext also nicht entschlüsseln oder gar das gesamte Verfahren brechen. Shannon konnte beweisen, dass das One-Time-Pad perfekt sicher ist.[1]

Asymptotische Sicherheit

Ein informationstheoretischer Beweis garantiert Sicherheit auch gegen Angreifer, die in ihrer Rechenleistung nicht beschränkt sind. Ein solcher Angreifer könnte jedoch bei einem Verfahren wie AES einfach alle möglichen Schlüssel durchprobieren. Mit real existierenden Computern würde das aber zu lange dauern. Um den Sicherheitsbegriff realistischer zu gestalten, wird daher der Angreifer in seiner Rechenleistung beschränkt, und zwar abhängig von der verwendeten Schlüssellänge (bzw. einem Sicherheitsparameter). Dann wird gezeigt, dass das System gegen einen solchen Angreifer sicher ist. Gezeigt wird also nur, dass der Aufwand für einen Angreifer sehr viel schneller wächst, als der Aufwand für die Benutzer. Durch passendes Wählen der Schlüssellänge können Angriffe so praktisch ausgeschlossen werden. Die Schlüssellänge muss aber der verfügbaren Rechenkraft angepasst werden, was einer der Gründe dafür ist, dass die früher für RSA verwendete Schlüssellänge von 768 Bit heute als unsicher gilt. Weil hier nur das asymptotische Verhalten untersucht wird, heißt die Sicherheit ebenfalls asymptotisch oder komplexitätstheoretisch.

Für die meisten kryptographischen Verfahren kann die Sicherheit des Systems nicht ohne weitere Annahmen bewiesen werden. Eine der frühesten verwendeten Annahmen ist die, dass das Faktorisierungsproblem schwer ist. Der Sicherheitsbeweis ist dann eine Reduktion zwischen dem Brechen des Systems und dem Lösen des Problems. Beispielsweise lässt sich beweisen, dass jeder Angreifer, der aus dem öffentlichen Schlüssel des RSA-Kryptosystems den geheimen berechnen kann, auch das Faktorisierungsproblem lösen kann (genauer gesagt, lässt sich aus einem erfolgreichen Angreifer ein effizienter Löser konstruieren). Da es einen solchen Löser laut Annahme aber nicht geben kann, kann es auch keinen erfolgreichen Angreifer geben. Sicherheit bedeutet hier also nicht mehr, dass es für den Angreifer völlig unmöglich ist, das System zu brechen, sondern dass dies praktisch unmöglich ist. Anders ausgedrückt, ist seine Erfolgswahrscheinlichkeit vernachlässigbar klein.

Konkrete Sicherheit

Bei asymptotischen Sicherheitsbeweisen wird nur gezeigt, dass ein System ab einem gewissen Wert des Sicherheitsparameters (der Schlüssellänge) sicher ist. Will man ein solches System instanziieren, muss aber ein konkreter Parameter gewählt werden. Dazu muss der Beweis genauer geführt und für die Erfolgswahrscheinlichkeit des Angreifers in Abhängigkeit von den benutzten Ressourcen (Laufzeit, Anzahl der Orakelanfragen) eine enge obere Schranke angegeben werden. Kann eine solche Abhängigkeit angegeben werden, spricht man von konkreter Sicherheit.

Beispiel

Der Simulator S erzeugt aus dem Problem P das IND-CPA-„Interface“ für den Angreifer A

Das Elgamal-Verschlüsselungsverfahren ist IND-CPA-sicher unter der Annahme, dass das Decisional-Diffie-Hellman-Problem schwierig ist. Der Beweis besteht aus einer Reduktion, in der aus jedem erfolgreichen Angreifer gegen die Sicherheit des Systems ein Löser für das DDH-Problem konstruiert wird. Weil DDH als schwer angenommen wurde, ist damit klar, dass ein solcher Angreifer nicht existieren kann.

Gegeben ist ein Angreifer A, von dem nichts bekannt ist, außer dass er gegen ElGamal das IND-CPA-Experiment gewinnt. Wenn er also einen öffentlichen Schlüssel erhält, gibt er zwei Nachrichten $m_{0},m_{1}$ aus. Gibt man ihm dann die Verschlüsselung einer der beiden unter dem öffentlichen Schlüssel, kann er mit Wahrscheinlichkeit $1/2+\epsilon$ sagen, welche Nachricht verschlüsselt wurde.

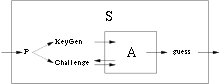
Aus diesem Angreifer A konstruiert man nun wie folgt einen Löser S für DDH. Dieser erhält eine Beschreibung einer Gruppe mit Erzeuger $g$ und ein Tripel $(g^{x},g^{y},g^{z})$ als Eingabe. S simuliert nun die Schlüsselerzeugung und gibt $g^{x}$ als öffentlichen Schlüssel an A. Den dazugehörigen geheimen Schlüssel kennt S nicht, aber das kann A nicht wissen. A gibt nach einiger Zeit zwei Nachrichten $m_{0},m_{1}$ aus. S muss nun die Verschlüsselung simulieren. Er wählt ein zufälliges Bit $b$ und setzt das Chiffrat zu $g^{y},g^{z}m_{b}$ . Der Angreifer A gibt daraufhin ein bit $b'$ zurück. Ist nun $g^{z}=g^{xy}$ , so ist das Chiffrat von einem normal erzeugten nicht zu unterscheiden. Ist $g^{z}$ ein zufälliges Gruppenelement, so kann der Angreifer nur raten und gewinnt mit Wahrscheinlichkeit 1/2. Die Strategie von S ist daher wie folgt: War A erfolgreich und gibt das richtige Bit zurück, so vermutet S, dass $g^{z}=g^{xy}$ . Liegt A falsch, so vermutet S, dass $g^{z}$ ein zufälliges Element war. Die Erfolgswahrscheinlichkeit von S liegt dann bei $1/2+\epsilon /2$ .

Diskussion

Das Paradoxon der beweisbaren Sicherheit ist, dass ein als sicher bewiesenes System nicht notwendigerweise wirklich sicher ist. Das liegt daran, dass für einen Beweis mehrere Annahmen und Formalisierungen nötig sind. Das System, der Angreifer und das Sicherheitsziel müssen formal beschrieben werden (wie beispielsweise IND-CPA Sicherheit für Verschlüsselungen) und der Beweis ist nur eine Reduktion eines Problems, dessen Schwere angenommen wurde. Ein Angreifer, der stärker ist als der im Beweis angenommene, kann das System also möglicherweise brechen. Genauso kann es vorkommen, dass das Sicherheitsziel nicht ausreichend formuliert wurde, also dem Angreifer schon ein geringerer Erfolg ausreicht. Wenn das Sicherheitsziel beispielsweise ist „Kein Angreifer soll aus einem Geheimtext den Klartext ableiten können“, so trifft der Beweis keine Aussage über einen Angreifer, der nur die ersten drei Buchstaben des Klartextes erfahren will. Ein weiteres Problem ist, dass das reale Kryptosystem nicht genau das formale abbildet, weil entweder bei der Implementierung des formalen oder bei der Formalisierung eines bereits existierenden Systems Fehler gemacht wurden. Ein eher unwahrscheinlicher Weg, das System dennoch zu brechen, ist das Lösen des mathematischen Problems, das der Sicherheit zugrunde liegt. Zu guter Letzt kann natürlich auch einfach der Beweis falsch sein. Trotz dieser zahlreichen Probleme sind Sicherheitsbeweise in der modernen Kryptologie ein wertvolles Hilfsmittel.

Einzelnachweise

Claude Shannon: Communication Theory of Secrecy System. In: Bell System Technical Journal. Band 28, Nr. 4, 1949, S. 656–715 (netlab.cs.ucla.edu [PDF; 549 kB]).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Claude Shannon: Communication Theory of Secrecy System. In: Bell System Technical Journal. Band 28, Nr. 4, 1949, S. 656–715 (netlab.cs.ucla.edu [PDF; 549 kB]).