Einschwingvorgang

Der Einschwingvorgang, engl. transient, in Naturwissenschaft und Technik gibt das zeitliche Verhalten eines Systems nach dem Einsetzen einer äußeren Anregung wieder.[1][2] Bei Anregung eines stationären Vorgangs durch eine sprunghafte Veränderung stellt sich eine freie Schwingung ein und infolge einer Dämpfung abklingend (schwingend) oder aperiodisch (kriechend) ein neuer stationärer Vorgang. Bei Kompensation der Dämpfung kann die freie Schwingung auch eine Dauerschwingung sein. Bei periodischer Anregung stellt sich ein Übergang in eine stationäre erzwungene Schwingung ein. Wenn der Ausgleichsvorgang praktisch abgeschlossen ist, nimmt das System einen eingeschwungenen Zustand an.[3][4]

Gedämpfte Sprungantwort, die mit Überschwingen einem Ruhezustand zustrebt

Anregung und Einschaltvorgang eines gering gedämpften Reihenschwingkreises bei Übereinstimmung von Anregungs- und Resonanzfrequenz[5][6]

Einschaltvorgang, der am Zeitpunkt des Minimums einer stationären Wechselspannung beginnt[5][6]
oben bei

f_{\text{frei}}\ll f_{\text{stat}}

unten bei

f_{\text{frei}}\gg f_{\text{stat}}

Die jeweils mittlere Linie zeigt oben die freie Spannung, unten die stationäre

Einschwingvorgang eines Schmalbandfilters nach Anlegen einer plötzlich eingeschalteten Sinusschwingung[7]

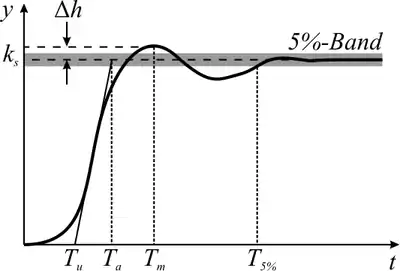
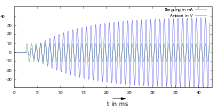
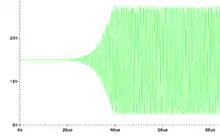
Kennzeichen

Der Einschwingvorgang eines Systems ist die Folge einer Stetigkeitsanforderung, die besagt, dass sich die im System gespeicherte Energie nicht sprunghaft ändern kann.[8] Bei nur einem Energiespeicher, beispielsweise einem RC-Glied, ist der Einschwingvorgang aperiodisch[9]. Kann Energie auf verschiedene Art gespeichert und ausgetauscht werden, beispielsweise in einem Pendel mit kinetischer und potentieller Energie, kann der Vorgang auch schwingend verlaufen.

Der Einschwingvorgang verrät die schwingungsphysikalischen Eigenschaften des Systems im Zeit- und damit auch im Frequenzbereich. Aus diesem Grunde kann dieser Vorgang zur Systemanalyse herangezogen werden. Während des Einschwingens liefert das System Information über sich selbst.[1]

Bei linearen Schwingungssystemen ist die Einschwingzeit dem Abklingkoeffizienten umgekehrt proportional. Der Einschwingvorgang klingt umso langsamer ab, je schwächer das System gedämpft ist. In Resonanzsystemen, Filtern und weiteren Schwingungssystemen dauert der Einschwingvorgang daher umso länger, je geringer ihre Frequenzbandbreite ist.[10] Die Einschwingzeit des Bandpasses begrenzt beispielsweise die Analysiergeschwindigkeit von Spektralanalysatoren, die nach dem Superpositionsprinzip arbeiten.

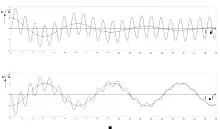
Im Einschwingvorgang linearer gedämpfter Schwingungssysteme mit sinusförmiger Anregung überlagern sich die stationäre erzwungene Schwingung und die exponentiell gedämpfte freie Schwingung, siehe nebenstehendes Doppelbild. Die Werte der Parameter der freien Schwingungen werden durch die Anfangsbedingungen festgelegt. Das Bild zeigt, dass im Einschaltaugenblick die Spannung auf der Höhe null beginnt, obwohl die eingeschaltete Wechselspannung zu diesem Zeitpunkt ihr Minimum hat. Die eingeschaltete Spannung erreicht in beiden Fällen fast das Doppelte der Amplitude ${\hat {u}}$ der stationären Spannung.

Zur quantitativen Behandlung von Einschwingvorgängen in linearen Systemen eignet sich besonders die Laplace-Transformation, weil sie die den Einschwingvorgang beschreibenden Differentialgleichungen durch algebraische Gleichungen ersetzt und die Anfangsbedingungen von vornherein berücksichtigt.

Der eingeschwungene Zustand ist frei von anfänglichen oder nichtstationären Eingangssignalen; in diesem Zustand ist ein System stabil. Die Zustandsvariablen des Systems (bei Wechselgrößen deren Amplitude, Frequenz und Phasenverschiebung) werden konstant. Ein eingeschwungener Zustand darf nicht gleichgesetzt werden mit dem Zustand einer Dauerschwingung. Bei vorhandener Dämpfung und ohne periodische Anregung schwingt der Vorgang in einen ruhenden Zustand ein.

Beispiele

Schaltvorgänge im elektrischen Energieversorgungsnetz können mit sehr steil ansteigenden „transienten“ Schwingungen und hohen Amplituden Überspannungen auslösen, die nach kurzer Zeit auf die (erzwungene) Netzschwingung abklingen. Hochspannungsschalter werden besonders ausgerüstet, um den Einschwingvorgang zu dämpfen.[11]

Auch Messgeräte unterliegen Einschwingvorgängen.[12] Während sich z. B. bei mechanischen Waagen und Drehspulgeräten das Ende des Einschwingens in die Ruhelage oft gut beobachten lässt, ist das Ende des stets kriechenden Übergangs bei Berührungsthermometern schwerer abschätzbar. Genauso, nur in einem anderen Zeitrahmen, unterliegen Digital-Analog-Umsetzer der einschwingenden Reaktion auf zwangsläufig sprunghafte Veränderungen des digitalen Eingangssignals.[13] Mit zunehmender Auflösung muss eine längere Entscheidungszeit der Komparatoren abgewartet werden.[14][15]

Manche Vorgänge, wie z. B. die durch Erdbeben hervorgerufenen Schwingungen von Bauwerken, laufen in so kurzer Zeit ab, dass die Anregung in kürzerer Zeit als der Einschwingzeit verschwindet. Die gleichwohl ausgelösten freien Schwingungen dürfen keineswegs außer Acht gelassen werden.[16]

In der Akustik und Musik ist es oft der Einschwingvorgang, z. B. der Bogenanstrich einer Saite, der den Klang eines Musikinstruments für unser Ohr eindeutig identifiziert. Die Anregung kommt durch das Anschlagen oder die Auslenkung einer Saite aus dem Ruhezustand. Ist ihre Schwingung nicht mehr von Auslenkung (Anfangsbedingung) oder Anschlagen (Eingangsimpuls) abhängig, hat sich der Systemzustand eingeschwungen. Der eigentliche Anfang des Klangverlaufs ist von überragender Bedeutung.[17]

Ein Beispiel für nichtstationäre Anregungen ist das Musizieren auf der Saite: Es gibt keine klare Regel, wann die Saite wie stark und in welcher Frequenz angeschlagen wird. Der Zustand des Systems kann deswegen als instationär bezeichnet werden. Sind die Einflüsse abgeklungen, so befindet sich das System wieder in einem eingeschwungenen Zustand.

Weblinks

Angela Schwenk: Die erzwungene Schwingung - Einschwingvorgang. In: Autoren-Website. Beuth Hochschule für Technik Berlin, 1. April 2009, abgerufen am 3. Juli 2016 (Visualisierung für verschiedene starke Dämpfung).

Einzelnachweise

Ulrich Karrenberg: Signale – Prozesse – Systeme: Eine multimediale und interaktive Einführung in die Signalverarbeitung. Springer Vieweg, 7. Aufl., 2017, S. 182
Jörg Hugel: Elektrotechnik: Grundlagen und Anwendungen. Teubner, 1998, S. 368
Harald Schumny: Signalübertragung: Lehrbuch der Nachrichtentechnik und Datenfernverarbeitung. Vieweg, 1978, S. 157
Hans Fricke, Kurt Lamberts, Ernst Patzelt: Grundlagen der elektrischen Nachrichtenübertragung. Teubner, 1979, S. 37
Steffen Paul, Reinhold Paul: Grundlagen der Elektrotechnik und Elektronik 3: Dynamische Netzwerke: zeitabhängige Vorgänge, Transformationen, Systeme. Springer Vieweg, 2017, S. 842
Erwin Meyer, Dieter Guicking: Schwingungslehre. Vieweg, 1974, S. 345
Erwin Meyer, Dieter Guicking: Schwingungslehre. Vieweg, 1974, S. 351
Reinhold Paul, Steffen Paul: Repetitorium Elektrotechnik: Elektromagnetische Felder, Netzwerke, Systeme. Springer, 1996, S. 510
Rolf Unbehauen: Grundlagen der Elektrotechnik 2: Einschwingvorgänge, Nichtlineare Netzwerke, Theoretische Erweiterungen., Springer, 5. Aufl., 2000, S. 1 ff
Erwin Meyer, Dieter Guicking: Schwingungslehre. Vieweg, 1974, S. 346
Valentin Crastan: Elektrische Energieversorgung 1: Netzelemente, Modellierung, stationäres Verhalten, Bemessung, Schalt- und Schutztechnik., Springer. 2. Aufl., S. 599
Herbert Bernstein: Werkbuch der Messtechnik: Messen mit analogen, digitalen und PC-Messgeräten in Theorie und Praxis. Franzis, 2010, S. 27 ff
Ekbert Hering, Klaus Bressler, Jürgen Gutekunst: Elektronik für Ingenieure. Springer, 4 Aufl., 2001, S. 381
Horst Germer, Norbert Wefers: Meßelektronik 2: Digitale Signalverarbeitung, Mikrocomputer, Meßsysteme. Hüthig, 1986, S. 95 f
Jürgen Winfried Klein, Peter Dullenkopf, Albrecht Glasmachers: Elektronische Meßtechnik: Meßsysteme und Schaltungen. Teubner, 1992, S. 140
Karl Klotter: Einfache Schwinger und Schwingungsmeßgeräte. Springer, 2. Aufl., 1951, S. 218
Charles Taylor: Der Ton macht die Physik: Die Wissenschaft von Klängen und Instrumenten. Vieweg, 1994, S. 92

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Karrenberg-1] Ulrich Karrenberg: Signale – Prozesse – Systeme: Eine multimediale und interaktive Einführung in die Signalverarbeitung. Springer Vieweg, 7. Aufl., 2017, S. 182

[2] Jörg Hugel: Elektrotechnik: Grundlagen und Anwendungen. Teubner, 1998, S. 368

[3] Harald Schumny: Signalübertragung: Lehrbuch der Nachrichtentechnik und Datenfernverarbeitung. Vieweg, 1978, S. 157

[4] Hans Fricke, Kurt Lamberts, Ernst Patzelt: Grundlagen der elektrischen Nachrichtenübertragung. Teubner, 1979, S. 37

[PP-5] Steffen Paul, Reinhold Paul: Grundlagen der Elektrotechnik und Elektronik 3: Dynamische Netzwerke: zeitabhängige Vorgänge, Transformationen, Systeme. Springer Vieweg, 2017, S. 842

[Meyer-6] Erwin Meyer, Dieter Guicking: Schwingungslehre. Vieweg, 1974, S. 345

[7] Erwin Meyer, Dieter Guicking: Schwingungslehre. Vieweg, 1974, S. 351

[8] Reinhold Paul, Steffen Paul: Repetitorium Elektrotechnik: Elektromagnetische Felder, Netzwerke, Systeme. Springer, 1996, S. 510

[9] Rolf Unbehauen: Grundlagen der Elektrotechnik 2: Einschwingvorgänge, Nichtlineare Netzwerke, Theoretische Erweiterungen., Springer, 5. Aufl., 2000, S. 1 ff

[10] Erwin Meyer, Dieter Guicking: Schwingungslehre. Vieweg, 1974, S. 346

[11] Valentin Crastan: Elektrische Energieversorgung 1: Netzelemente, Modellierung, stationäres Verhalten, Bemessung, Schalt- und Schutztechnik., Springer. 2. Aufl., S. 599

[12] Herbert Bernstein: Werkbuch der Messtechnik: Messen mit analogen, digitalen und PC-Messgeräten in Theorie und Praxis. Franzis, 2010, S. 27 ff

[13] Ekbert Hering, Klaus Bressler, Jürgen Gutekunst: Elektronik für Ingenieure. Springer, 4 Aufl., 2001, S. 381

[14] Horst Germer, Norbert Wefers: Meßelektronik 2: Digitale Signalverarbeitung, Mikrocomputer, Meßsysteme. Hüthig, 1986, S. 95 f

[15] Jürgen Winfried Klein, Peter Dullenkopf, Albrecht Glasmachers: Elektronische Meßtechnik: Meßsysteme und Schaltungen. Teubner, 1992, S. 140

[16] Karl Klotter: Einfache Schwinger und Schwingungsmeßgeräte. Springer, 2. Aufl., 1951, S. 218

[17] Charles Taylor: Der Ton macht die Physik: Die Wissenschaft von Klängen und Instrumenten. Vieweg, 1994, S. 92