Alternierendes Knotendiagramm

Im mathematischen Gebiet der Knotentheorie ist ein alternierendes Knotendiagramm ein Knotendiagramm, bei dessen Durchlaufen man abwechselnd Über- und Unterkreuzungen durchläuft. Analog ist ein alternierendes Verschlingungsdiagramm ein Verschlingungsdiagramm, für das sich beim Durchlaufen jeder Komponente jeweils Über- und Unterkreuzungen abwechseln.

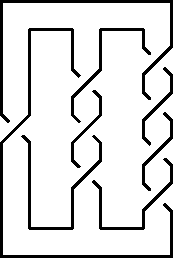
Ein alternierendes Knotendiagramm.

Ein alternierender Knoten ist ein Knoten, der sich zu einem alternierende Knotendiagramm in der Ebene projizieren lässt. (Nicht jede Projektion muss ein alternierendes Diagramm geben.) Entsprechend ist eine Verschlingung eine alternierende Verschlingung, wenn sie ein alternierendes Verschlingungsdiagramm besitzt.

Kreuzungszahl

Ein alternierendes Diagramm heißt reduziert, wenn an jeder Kreuzung vier unterschiedliche Regionen anliegen. Ein reduziertes alternierendes Diagramm berechnet die Kreuzungszahl, d. h. es ist das Diagramm minimaler Kreuzungszahl für den gegebenen Knoten.[1]

Flype: ein Tangle innerhalb des Knotendiagramms wird um 180⁰ gedreht

Eindeutigkeit

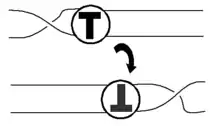
Je zwei reduzierte alternierende Diagramme desselben orientierten Knotens gehen durch eine Folge von Flypes (Drehungen eines Tangles um 180°) auseinander hervor.[2] Damit lässt sich leicht entscheiden, ob zwei alternierende Diagramme denselben Knoten darstellen.

Seifert-Fläche

Der Seifert-Algorithmus liefert für alternierende Knoten und Verschlingungen eine Seifert-Fläche minimalen Geschlechts $g$ . Insbesondere gilt für alternierende Verschlingungen die Gleichung $d=2g$ , wobei $d$ den Grad des Alexander-Polynoms bezeichnet.[3][4][5]

Twist-Zahl und hyperbolisches Volumen

Alternierende Primknoten sind hyperbolisch.[6] Das hyperbolische Volumen eines hyperbolischen Knotens kann durch die Twistzahl (d. h. Anzahl der Twist-Regionen) $tw(D)$ eines alternierenden Diagramms abgeschätzt werden:[7]

{\frac {1}{2}}v_{3}tw(D)-1<vol(S^{3}\setminus K)<10v_{3}(tw(D)-1)

,

wobei $v_{3}$ die Gieseking-Konstante bezeichnet.

Literatur

Colin Adams: The Knot Book: An elementary introduction to the mathematical theory of knots. American Mathematical Society, Providence, RI, 2004, ISBN 0-8218-3678-1.

Weblinks

Alternating Knot (MathWorld)

Einzelnachweise

Kunio Murasugi: Jones polynomials and classical conjectures in knot theory. Topology 26 (1987), no. 2, 187–194.
William Menasco, Morwen Thistlethwaite: The Tait flyping conjecture. Bull. Amer. Math. Soc. (N.S.) 25 (1991), no. 2, 403–412; The classification of alternating links. Ann. of Math. (2) 138 (1993), no. 1, 113–171.
Kunio Murasugi: On the genus of the alternating knot. I, II. J. Math. Soc. Japan 10 1958 94–105, 235–248.
Richard Crowell: Genus of alternating link types. Ann. of Math. (2) 69 1959 258–275.
David Gabai: Genera of the alternating links. Duke Math. J. 53 (1986), no. 3, 677–681.
William Menasco: Closed incompressible surfaces in alternating knot and link complements. Topology 23 (1984), no. 1, 37–44.
Marc Lackenby: The volume of hyperbolic alternating link complements. With an appendix by Ian Agol and Dylan Thurston. Proc. London Math. Soc. (3) 88 (2004), no. 1, 204–224.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Kunio Murasugi: Jones polynomials and classical conjectures in knot theory. Topology 26 (1987), no. 2, 187–194.

[2] William Menasco, Morwen Thistlethwaite: The Tait flyping conjecture. Bull. Amer. Math. Soc. (N.S.) 25 (1991), no. 2, 403–412; The classification of alternating links. Ann. of Math. (2) 138 (1993), no. 1, 113–171.

[3] Kunio Murasugi: On the genus of the alternating knot. I, II. J. Math. Soc. Japan 10 1958 94–105, 235–248.

[4] Richard Crowell: Genus of alternating link types. Ann. of Math. (2) 69 1959 258–275.

[5] David Gabai: Genera of the alternating links. Duke Math. J. 53 (1986), no. 3, 677–681.

[6] William Menasco: Closed incompressible surfaces in alternating knot and link complements. Topology 23 (1984), no. 1, 37–44.

[7] Marc Lackenby: The volume of hyperbolic alternating link complements. With an appendix by Ian Agol and Dylan Thurston. Proc. London Math. Soc. (3) 88 (2004), no. 1, 204–224.