A. J. W. Duijvestijn

A. J. W. Duijvestijn (* 10. Dezember 1927 in Den Haag als Adrianus Johannes Wilhelmus Duijvestijn; † 21. Januar 1998 in Enschede), auch Arie Duijvestijn oder AJW Duijvestijn genannt, war ein niederländischer Informatiker und Mathematiker.

A. J. W. Duijvestijn 1989

Leben

Duijvestijn studierte Elektrotechnik in Delft und schloss 1950 mit dem Master of Science ab. 1951 wechselte er an das mathematische Zentrum der Universität von Amsterdam, wo er – nach einer zweijährigen Unterbrechung durch den Militärdienst als Marineoffizier – 1955 den Masterabschluss in Mathematik erwarb. Hier erlernte er auf zu dieser Zeit noch recht primitiven Rechenautomaten das Programmieren. 1956 trat er in den Dienst des Philips Natuurkundig Laboratorium in Eindhoven ein. Die Zeit von November 1957 bis Mai 1958 verbrachte Duijvestijn in den USA bei IBM in Poughkeepsie und Gaithersburg; 1963 ging er zu Philips nach Apeldorn.

1962 promovierte Duijvestijn bei seinem Doktorvater C. J. Bouwcamp zum Ph.D. an der Technischen Universität Eindhoven mit einer Dissertation mit dem Titel „Electronic computation of squared rectangles“.[1] 1965 wurde er ordentlicher Professor für Informatik an der Universität Twente, an der er bis zu seiner Emeritierung im Jahr 1989 blieb. Von 1977 bis 1981 war Duijvestijn Präsident der Nederlands Genootschap voor Informatica.

Seit 1953 war Duijvestijn verheiratet; er wurde Vater von vier Kindern.

Besondere Leistung

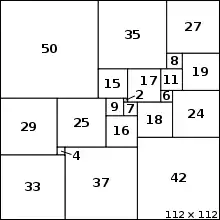
Einfache, perfekte Quadratur der geringstmöglichen Ordnung (21)

Bereits 1962 in seiner Dissertation hatte sich Duijvestijn mit dem Problem der Parkettierung von Rechtecken mit quadratischen Kacheln befasst. In den folgenden Jahren machte er sich mit Computerhilfe auf die Suche nach dem Spezialfall der perfekten, einfachen Quadratur des Quadrates, scheiterte aber immer wieder an der unzulänglichen Rechenleistung der damaligen Computertechnologie. 1978 schließlich stand ihm mit der PDP-10 von DEC ein ausreichend leistungsfähiger Computer zur Verfügung und er fand die perfekte, einfache Quadratur der Ordnung 21 (s. Abbildung). Er lieferte zudem den Beweis, dass dies die Lösung der geringstmöglichen Ordnung und zugleich die einzige dieser Ordnung ist.[2]

Schriften (Auswahl)

Electronic computation of squared rectangles. Dissertation, Technische Universität Eindhoven 1962. Online (Digitalisat)
Simple perfect square of lowest order. Universität Twente 1978. Online (Digitalisat)
Simple Perfect Squared Squares and 2 × 1 Squared Rectangles of Orders 21 to 24. Universität Twente 1992. Online (Digitalisat)
Catalogue of simple perfect squared squares of orders 21 through 25. Technische Universität Eindhoven 1992 (zusammen mit C. J. Bouwcamp). Online (Digitalisat)
Simple perfect squared squares and 2 × 1 squared rectangles of order 26. Universität Twente 1996. Online

Einzelnachweise

Duijvestijn 1962
Duijvestijn 1978

Literatur

Jasper Dale Skinner: Squared squares: Who's who & what's what. Eigenverlag, 1993, ISBN 0-9636569-0-2.

Weblinks

Adrianus Johannes Wilhelmus Duijvestijn (AJWD) (1927–1998). Ausführliche Biographie mit Fotos und Werkliste von Stuart Anderson (englisch)
In memoriam Arie Duijvestijn (Memento vom 5. April 2005 im Internet Archive). Nachruf (1998) der Universität Twente im Internet Archive (niederländisch)
Adrianus Johannes Wilhelmus Duijvestijn im Mathematics Genealogy Project

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Duijvestijn 1962

[2] Duijvestijn 1978