Wertetabelle

Unter einer Wertetabelle versteht man in der Mathematikdidaktik eine Tabelle mit zwei Spalten oder zwei Zeilen, in die Argumente und die dazugehörigen Funktionswerte einer Funktion eingetragen werden.

Wertetabellen können eingesetzt werden, um den Graphen einer Funktion zu erstellen. Hierdurch können nur diskrete Werte angegeben werden. Es geht daraus nicht hervor, wie sich die Funktion zwischen zwei Wertepaaren verhält.

Funktionen, die nur auf einer endlichen Menge definiert sind, können durch eine Wertetabelle der klassischen Aussagenlogik und auch einigen anderen Logiken Wertetabellen dazu verwendet, die semantischen Eigenschaften der logischen Verknüpfungszeichen zu charakterisieren.

In den empirischen Wissenschaften, etwa in der Physik, ist eine Wertetabelle, in der einzelne Messergebnisse erfasst werden, umgekehrt die Grundlage, um Vermutungen über einen dahinter stehenden Zusammenhang in Form einer mathematischen Funktion aufzustellen. Dies geschieht wiederum häufig, indem die Tabelleneinträge grafisch aufbereitet werden und dann Punkte „offensichtlich“ auf einer Geraden oder einer anderen einfachen Kurve liegen. Zusätzlich spielen hier statistische Verfahren wie etwa die Regressionsanalyse eine Rolle.

Beispiele

Aus der Wertetabelle für

y=x^{2}

gewonnene Punkte und zugehörige Kurve.

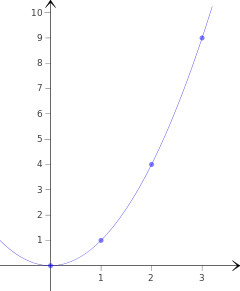
Zum Zeichnen des Graphen von $y=f(x)=x^{2}$ wird eine Wertetabelle für $\{x\in \mathbb {Z} \ |\ 0\leq x\leq 3\}$ erstellt.

x	f(x)
0	0
1	1
2	4
3	9

Um den Kurvenverlauf genauer zeichnen zu können, sind weitere Zwischenwerte hilfreich.

Aus der Wertetabelle für

y=(x^{2}-2)^{2}-1

gewonnene Punkte und zugehörige Kurve.

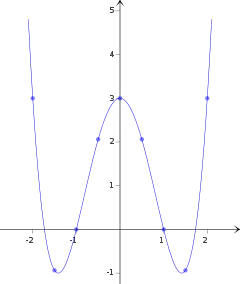
Zum Zeichnen des Graphen von $y=g(x)=(x^{2}-2)^{2}-1$ wird eine Wertetabelle für einige x-Werte von −3 bis +3 erstellt.

x	−3	−2	−3/2	−1	−1/2	0	1/2	1	3/2	2	3
g(x)	48	3	−15/16	0	33/16	3	33/16	0	−15/16	3	48

Die Wertetabelle legt (richtigerweise) nahe, dass der Graph von g symmetrisch zur y-Achse ist. Dies ist jedoch formal zu überprüfen. Die Tabelle legt auch nahe, dass bei $x=0$ ein lokales Maximum und bei $x=1{,}5$ sowie $x=-1{,}5$ je ein lokales Maximum liegt. Auch hier ist eine formale Überprüfung wichtig, denn nur die erste dieser Aussagen trifft tatsächlich zu. Allerdings darf man – Stetigkeit vorausgesetzt – aus der Tabelle wenigstens schließen, dass zwischen −2 und −1 bzw. zwischen 1 und 2 je (mindestens) ein lokales Minimum liegt (die lokalen Minima liegen in der Tat bei $x=\pm {\sqrt {2}}$ ). Schließlich sieht man noch, dass bei $x=-1$ und $x=+1$ eine Nullstelle liegt, sowie dass (wiederum Stetigkeit vorausgesetzt), zwischen −2 und −1,5 sowie zwischen 1,5 und 2 jeweils mindestens eine Nullstelle liegen muss. Hier liefert also die Wertetabelle einen wertvollen Ausgangspunkt für die numerische Nullstellensuche etwa mit dem Sekantenverfahren (tatsächlich liegen diese beiden Nullstellen bei $x=\pm {\sqrt {3}}$ ). Jedoch kann man allgemein nicht davon ausgehen, jede Nullstelle von g so über eine einfache Wertetabelle aufzuspüren. Im vorliegenden Fall hat man allerdings dennoch alle Nullstellen gefunden, da ein Polynom vierten Grades nur vier Nullstellen haben kann.

Bei Wertetabellen für logische Funktionen spricht man auch von einer Wahrheitstabelle. Die XOR-Funktion wird beispielsweise durch folgende Wertetabelle definiert:

(A,B)	A XOR B
(FALSCH, FALSCH)	FALSCH
(FALSCH, WAHR)	WAHR
(WAHR, FALSCH)	WAHR
(WAHR, WAHR)	FALSCH

Hier bedeutet die dritte Zeile: Wenn A wahr ist, und B Falsch, dann ist „A XOR B“ auch wahr.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.