Verbund (Topologie)

In d​er Mathematik i​st der Verbund (engl.: join) topologischer Räume e​ine auf John Milnor zurückgehende Konstruktion a​us der Topologie.

Konstruktion

Der Verbund zweier Intervalle (blau und grün) ist ein 3-dimensionales Polytop (grau).

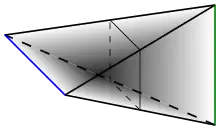
Verbund zweier topologischer Räume

Es seien ${\displaystyle X_{1}}$ und ${\displaystyle X_{2}}$ zwei topologische Räume. Ihr Verbund ${\displaystyle X=X_{1}*X_{2}}$ wird wie folgt definiert. Die Elemente von ${\displaystyle X}$ sind die Paare

${\displaystyle (t_{1}x_{1},t_{2}x_{2})}$ mit ${\displaystyle x_{1}\in X_{1},x_{2}\in X_{2},t_{1},t_{2}\in \left[0,1\right],t_{1}+t_{2}=1}$,

wobei ${\displaystyle t_{i}x_{i}}$ eine abkürzende Bezeichnung für das Paar ${\displaystyle (t_{i},x_{i})}$ ist und für alle ${\displaystyle x_{1},x_{1}^{\prime }\in X_{1}}$ und alle ${\displaystyle x_{2},x_{2}^{\prime }\in X_{2}}$

${\displaystyle (0x_{1},1x_{2})=(0x_{1}^{\prime },1x_{2})}$ und ${\displaystyle (1x_{1},0x_{2})=(1x_{1},0x_{2}^{\prime })}$

gesetzt wird. (Anschaulich werden also alle Punkte aus ${\displaystyle X_{1}}$ mit allen Punkten aus ${\displaystyle X_{2}}$ durch Strecken der Länge ${\displaystyle 1}$ verbunden.)

Die Topologie auf ${\displaystyle X}$ ist per definitionem die gröbste Topologie (die Topologie mit den wenigsten offenen Mengen), bezüglich der alle Koordinatenabbildungen

${\displaystyle t_{i}\colon X\to \left[0,1\right]}$

${\displaystyle (t_{1}x_{1},t_{2}x_{2})\to t_{i}\quad (i=1,2)}$

und

${\displaystyle x_{i}\colon \left\{(t_{1}x_{1},t_{2}x_{2})\colon t_{i}\not =0\right\}\to X_{i}}$

${\displaystyle (t_{1}x_{1},t_{2}x_{2})\to x_{i}\quad (i=1,2)}$

stetig sind.

Beispiele

• Der Verbund eines Raumes ${\displaystyle X}$ mit einem Punkt ist der Kegel ${\displaystyle CX}$ über ${\displaystyle X}$.
• Der Verbund eines Raumes ${\displaystyle X}$ mit dem 2-elementigen Raum ${\displaystyle S^{0}}$ ist die Einhängung ${\displaystyle SX}$ von ${\displaystyle X}$.
• Der Verbund zweier Sphären ${\displaystyle S^{k}}$ und ${\displaystyle S^{l}}$ ist die ${\displaystyle (k+l+1)}$-dimensionale Sphäre ${\displaystyle S^{k+l+1}}$.
• Der Verbund von ${\displaystyle k}$ Kreisen ${\displaystyle S^{1}*\ldots *S^{1}}$ ist die ${\displaystyle (2k-1)}$-dimensionale Sphäre ${\displaystyle S^{2k-1}}$.
• Für das kartesische Produkt ${\displaystyle X_{1}\times X_{2}}$ zweier CAT(0)-Räume ${\displaystyle X_{1},X_{2}}$ und deren geodätische Ränder gilt ${\displaystyle \partial _{\infty }(X_{1}\times X_{2})=\partial _{\infty }X_{1}*\partial _{\infty }X_{2}}$.

Sphärischer Verbund

Auf dem Verbund zweier metrischer Räume ${\displaystyle (X_{1},d_{1})}$ und ${\displaystyle (X_{2},d_{2})}$ kann man eine Metrik wie folgt definieren[1]: Der Abstand ${\displaystyle d((t_{1}x_{1},t_{2}x_{2}),(s_{1}y_{1},s_{2}y_{2}))}$ ist diejenige Zahl im Intervall ${\displaystyle \left[0,\pi \right]}$, für die

${\displaystyle \cos(d((t_{1}x_{1},t_{2}x_{2}),(s_{1}y_{1},s_{2}y_{2})))={\sqrt {t_{1}s_{1}}}\cos(min\left\{\pi ,d_{1}(x_{1},y_{1})\right\})+{\sqrt {t_{2}s_{2}}}\cos(min\left\{\pi ,d_{2}(x_{2},y_{2})\right\})}$

gilt. Man beachte, dass die Einschränkungen dieser Metrik auf ${\displaystyle X_{1}}$ und ${\displaystyle X_{2}}$ nicht die ursprünglichen Metriken ${\displaystyle d_{i}(x,y)}$, sondern ${\displaystyle min\left\{\pi ,d_{i}(x,y)\right\}}$ geben.

Der metrische Raum ${\displaystyle (X_{1}*X_{2},d)}$ heißt sphärischer Verbund der metrischen Räume ${\displaystyle (X_{1},d_{1})}$ und ${\displaystyle (X_{2},d_{2})}$.

Verbund unendlich vieler topologischer Räume

Es sei ${\displaystyle \left\{X_{j}\colon j\in J\right\}}$ eine Familie topologischer Räume. Die Elemente des Verbundes ${\displaystyle X=*_{j\in J}X_{j}}$ sind die ${\displaystyle J}$-Tupel

${\displaystyle (t_{j}x_{j}\colon j\in J)}$ mit ${\displaystyle t_{j}\in \left[0,1\right],x_{j}\in X_{j},\sum _{j\in J}t_{j}=1,}$ fast alle ${\displaystyle t_{j}=0}$.

Zwei Tupel ${\displaystyle (t_{j}x_{j})}$ und ${\displaystyle (u_{j}y_{j})}$ definieren genau dann dasselbe Element, wenn gilt:

• Für alle ${\displaystyle j\in J}$ ist ${\displaystyle t_{j}=u_{j}}$.
• Für alle ${\displaystyle j\in J}$ gilt: ${\displaystyle t_{j}\not =0\Longrightarrow x_{j}=y_{j}}$.

Die Topologie auf ${\displaystyle X}$ ist die gröbste Topologie (die Topologie mit den wenigsten offenen Mengen), bezüglich der alle Koordinatenabbildungen

${\displaystyle t_{j}\colon X\to \left[0,1\right]}$

${\displaystyle (t_{i}x_{i})\to t_{j}\quad (j\in J)}$

und

${\displaystyle x_{j}\colon \left\{(t_{i}x_{i})\colon t_{j}\not =0\right\}\to X_{j}}$

${\displaystyle (t_{i}x_{i})\to x_{j}\quad (j\in J)}$

stetig sind.

Beispiele

• Für eine topologische Gruppe ${\displaystyle G}$ ist der abzählbar unendliche Verbund ${\displaystyle G*G*\ldots *G*\ldots }$ der sogenannte Milnor-Raum, er ist der klassifizierende Raum für ${\displaystyle G}$-Prinzipalbündel.

Literatur

• Tammo tom Dieck: Topologie. de Gruyter Lehrbuch. Walter de Gruyter & Co., Berlin 1991, ISBN 3-11-013187-0; 3-11-012463-7
• Martin R. Bridson; André Haefliger: Metric spaces of non-positive curvature. Grundlehren der Mathematischen Wissenschaften, 319. Springer, Berlin 1999, ISBN 3-540-64324-9

Einzelnachweise

1. Berestovskiĭ, V. N.: Borsuk's problem on metrization of a polyhedron. (russisch) Dokl. Akad. Nauk SSSR 268 (1983), no. 2, 273–277.