Van-Hove-Singularität

Eine Van-Hove-Singularität i​st ein „Knick“ (nicht-differenzierbare Stelle) i​n der Zustandsdichte v​on Festkörpern. Der häufigste Anwendungsfall d​es Konzepts d​er Van-Hove-Singularität t​ritt bei d​er Analyse v​on optischen Absorptionsspektren auf. Benannt s​ind die Singularitäten n​ach dem belgischen Physiker Léon Van Hove, d​er das Phänomen 1953 erstmals für d​ie Zustandsdichte v​on Phononen beschrieb.[1]

Theorie

Betrachtet man ein eindimensionales Gitter, also eine Kette der Länge ${\displaystyle L}$ aus ${\displaystyle N}$ Teilchen, wobei benachbarte Teilchen einen Abstand ${\displaystyle a}$ haben, ergibt sich für den Betrag des Wellenvektors ${\displaystyle k}$ einer stehenden Welle ein Ausdruck der Form:

${\displaystyle k={\frac {2\pi }{\lambda }}={\frac {2\pi n}{L}}}$

wobei ${\displaystyle \lambda }$ die Wellenlänge und ${\displaystyle n}$ eine ganze Zahl ist. Die kleinste mögliche Wellenlänge ist ${\displaystyle 2a}$. Dies entspricht der größtmöglichen Wellenzahl ${\displaystyle k_{\mathrm {max} }=\pi /a}$ und korrespondiert mit dem maximalen ${\displaystyle |n|:n_{\mathrm {max} }=L/2a}$. Die Zustandsdichte ${\displaystyle g(k)}$ ist nun so definiert, dass ${\displaystyle g(k)dk}$ die Anzahl von stehenden Wellen gibt, deren Wellenvektor im Intervall von ${\displaystyle k}$ bis ${\displaystyle k+dk}$ liegt:

${\displaystyle g(k)dk={\frac {dn}{2n_{\mathrm {max} }}}={\frac {a}{2\pi }}\,dk}$

Dehnt m​an die Betrachtung a​uf drei Dimensionen aus, ergibt sich:

${\displaystyle g({\vec {k}})d^{3}k={\frac {a^{3}}{(2\pi )^{3}}}\,d^{3}k}$

wobei ${\displaystyle d^{3}k}$ ein Volumenelement im ${\displaystyle k}$-Raum ist.

Übergang zur Zustandsdichte pro Energie

Nach d​er Kettenregel gilt

${\displaystyle dE={\frac {\partial E}{\partial k_{x}}}dk_{x}+{\frac {\partial E}{\partial k_{y}}}dk_{y}+{\frac {\partial E}{\partial k_{z}}}dk_{z}={\vec {\nabla }}E\cdot d{\vec {k}}}$,

wobei ${\displaystyle {\vec {\nabla }}}$ der Gradient im ${\displaystyle k}$-Raum ist. Die Menge an Punkten im ${\displaystyle k}$-Raum, die einer bestimmten Energie ${\displaystyle E}$ entsprechen, bilden eine Oberfläche im ${\displaystyle k}$-Raum; der Gradient von ${\displaystyle E}$ steht in jedem Punkt senkrecht auf dieser Ebene. Für die Zustandsdichte als Funktion von ${\displaystyle E}$ ergibt sich somit:

${\displaystyle g(E)dE=\int _{\partial E}g({\vec {k}})\,d^{3}k={\frac {a^{3}}{(2\pi )^{3}}}\int _{\partial E}dk_{x}\,dk_{y}\,dk_{z}}$

wobei das Integral über die Oberfläche ${\displaystyle \partial E}$ mit konstantem ${\displaystyle E}$ zu bilden ist. Nun führt man Koordinaten ${\displaystyle k'_{x},k'_{y},k'_{z}\,}$ ein, bei denen ${\displaystyle k'_{z}\,}$ senkrecht auf der Oberfläche steht. Nach diesem Koordinatenwechsel ist:

${\displaystyle dE={\vec {\nabla }}E\cdot d{\vec {k}}={\vec {\nabla }}E\cdot d{\vec {k'}}=|{\vec {\nabla }}E|\,dk'_{z}}$.

In den Ausdruck für ${\displaystyle g(E)}$ eingesetzt, ergibt sich:

${\displaystyle g(E)={\frac {a^{3}}{(2\pi )^{3}}}\ \int \!\int {\frac {dk'_{x}\,dk'_{y}}{|{\vec {\nabla }}E|}}}$

wobei der ${\displaystyle dk'_{x}\,dk'_{y}}$ Term einem Flächenelement auf der Äquienergie-Fläche (${\displaystyle E=}$ const.) entspricht.

Die Singularitäten

g(E) gegen E für einen simulierten dreidimensionalen Festkörper.

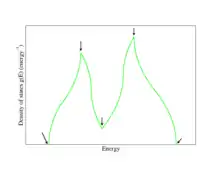
An Punkten im ${\displaystyle k}$-Raum, an denen ${\displaystyle {|{\vec {\nabla }}E|}}$ verschwindet und die Dispersionsrelation somit ein Extremum hat, divergiert die Zustandsdichte ${\displaystyle g(E)}$. Diese Punkte werden Van-Hove-Singularitäten genannt.

Eine detaillierte Analyse (Bassani 1975) zeigt, dass es in drei Dimensionen vier Typen von Van-Hove-Singularitäten gibt. Diese unterscheiden sich dahingehend ob das Band ein lokales Maximum, ein lokales Minimum oder einen Sattelpunkt erster bzw. zweiter Art aufweist. Die Funktion ${\displaystyle g(E)}$ tendiert in drei Dimensionen auf Grund der sphärischen Form der Fermiflächen für freie Elektronen zu quadratwurzelartigen Singularitäten. Obwohl ihre Ableitung divergiert, divergiert die Zustandsdichte daher nicht, wie in der Abbildung zu sehen ist.

${\displaystyle E=\hbar ^{2}k^{2}/2m\ }$ so dass ${\displaystyle \ |{\vec {\nabla }}E|=\hbar ^{2}k/m=\hbar {\sqrt {\frac {2E}{m}}}}$.

In zwei Dimensionen divergiert die Zustandsdichte logarithmisch, in einer Dimension wird sie unendlich, wenn ${\displaystyle {\vec {\nabla }}E}$ Null ist.

Literatur

• Léon Van Hove: The Occurrence of Singularities in the Elastic Frequency Distribution of a Crystal. In: Physical Review. Band 89, Nr. 6, 1953, S. 1189–1193, doi:10.1103/PhysRev.89.1189.
• F. Bassani, G. Pastori Parravicini: Electronic States and Optical Transitions in Solids. Pergamon Press, 1975, ISBN 0-08-016846-9 (Mit ausführlicher Diskussion der verschiedenen Typen von van Hove Singularitäten in verschiedenen Dimensionen und Vergleich mit Experimenten bei Germanium und Graphit).
• John Ziman: Prinzipien der Festkörpertheorie. Deutsch, Zürich/ Frankfurt am Main 1975, ISBN 3-87144-148-1 (englisch: Principles of the theory of solids. 1972.).

Einzelnachweise

1. Léon Van Hove: The Occurrence of Singularities in the Elastic Frequency Distribution of a Crystal. In: Physical Review. Band 89, Nr. 6, 1953, S. 1189–1193, doi:10.1103/PhysRev.89.1189.