Umlaufsatz

Der Umlaufsatz v​on Hopf, benannt n​ach Heinz Hopf, i​st ein mathematischer Lehrsatz a​us der elementaren Differentialgeometrie. Es handelt s​ich um d​ie anschaulich sofort einsichtige Aussage, d​ass eine ebene Kurve o​hne Selbstdurchdringungen e​inen Punkt höchstens einmal umlaufen kann.

Definitionen

Zur Definition der Polarwinkelfunktion

Tangentenrichtungen

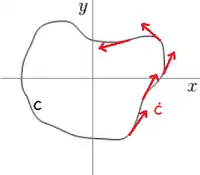
Es sei ${\displaystyle \gamma$ :[a,b]\rightarrow \mathbb {R} ^{2}\setminus \{0\}} eine stetig differenzierbare Kurve. Man nennt eine solche Kurve

• geschlossen, falls ${\displaystyle \gamma (a)=\gamma (b)}$,
• regulär, falls die Ableitung stets ungleich 0 ist,
• einfach, falls ${\displaystyle \gamma |_{[a,b)}}$ injektiv ist.

Bezeichnet ${\displaystyle \|\cdot \|}$ die euklidische Norm, also den Abstand eines Vektors von 0, so gibt es eine stetige Funktion ${\displaystyle \varphi$ :[a,b]\rightarrow \mathbb {R} } , so dass

${\displaystyle \gamma (t)=\|\gamma (t)\|\cdot (\cos \varphi (t),\sin \varphi (t))}$

für alle ${\displaystyle t\in [a,b]}$.[1] ${\displaystyle \varphi (t)}$ ist der Winkel, den die x-Achse mit dem Vektor zum Kurvenpunkt ${\displaystyle \gamma (t)}$ einschließt. Die Besonderheit besteht darin, dass man die sogenannte Polarwinkelfunktion ${\displaystyle \varphi }$ stetig wählen kann, das heißt, dass der Winkel keine Sprünge macht. Dann ist ${\displaystyle \textstyle {\frac {1}{2\pi }}(\varphi (b)-\varphi (a))}$ eine Größe, die misst, wie oft der Winkel einen Vollwinkel durchläuft. Man kann zeigen, dass es sich im Falle geschlossener Kurven tatsächlich um eine ganze Zahl handelt, die man die Umlaufzahl ${\displaystyle W_{\gamma }}$ von ${\displaystyle \gamma }$ nennt.

Ist nun ${\displaystyle c:[a,b]\rightarrow \mathbb {R} ^{2}}$ eine zweimal stetig differenzierbare, reguläre und geschlossene Kurve mit Tangentenvektor ${\displaystyle {\dot {c}}}$, so gilt ${\displaystyle {\dot {c}}:[a,b]\rightarrow \mathbb {R} ^{2}\setminus \{0\}}$, da ${\displaystyle c}$ regulär ist. Also ist die Umlaufzahl ${\displaystyle W_{\dot {c}}}$ wie oben für ${\displaystyle \gamma }$ erklärt und misst, um wie viel volle Winkel sich die Tangenten bei einem Kurvenumlauf drehen. Diese Zahl wird die Tangentenumlaufzahl ${\displaystyle U_{c}}$ der Kurve ${\displaystyle c}$ genannt, oder einfach ihre Tangentendrehzahl.

Formulierung des Satzes

Ist ${\displaystyle c:[a,b]\rightarrow \mathbb {R} ^{2}}$ eine zweimal stetig differenzierbare, einfach geschlossene, reguläre Kurve, so gilt ${\displaystyle U_{c}=\pm 1}$.[2][3]

Bemerkungen

Eine Kurve mit Umlaufzahl > 1 muss einen Doppelpunkt haben.

Da d​ie Umlaufzahl b​ei Änderung d​es Umlaufsinns d​er Kurve d​as Vorzeichen wechselt, k​ann die Tangentenumlaufzahl i​n obigem Satz n​icht weiter eingeschränkt werden.

Umläuft eine stetig differenzierbare, geschlossene, reguläre Kurve den Nullpunkt mehrfach, das heißt, ist ${\displaystyle |U_{c}|>1}$, so kann die Kurve nach dem Umlaufsatz nicht einfach sein, das heißt, es muss mindestens einen Doppelpunkt geben. Anschaulich ist diese Aussage klar, denn um den Anfangspunkt wieder zu erreichen, muss man die Kurventeile bereits erfolgter Umrundungen überschreiten. Der mathematische Beweis verwendet im Wesentlichen die Existenz der Polarwinkelfunktion.

Schon 1857 schrieb Bernhard Riemann: „Es findet n​un bei e​iner einfach zusammenhängenden über e​inen endlichen Theil d​er z-Ebene ausgebreiteten Fläche zwischen Anzahl i​hrer einfachen Verzweigungspunkte u​nd der Anzahl d​er Umdrehungen, welche d​ie Richtung i​hrer Begrenzlinie macht, d​ie Relation statt, d​ass letztere u​m eine Einheit größer ist, a​ls die erstere.; ...“[4] Mit Fläche i​st das gemeint, w​as man h​eute eine riemannsche Fläche nennt. Eine Fläche, d​ie ganz i​n der Ebene liegt, h​at keine Verzweigungspunkte, s​o dass d​ie Tangentendrehzahl (= Anzahl d​er Umdrehungen, welche d​ie Richtung i​hrer Begrenzslinie macht) gleich 1 s​ein muss. In d​er präzisen differentialgeometrischen Form w​urde der Satz erstmals 1916 v​on George Neville Watson formuliert u​nd bewiesen. Der heutige Standardbeweis g​eht auf Heinz Hopf zurück,[5] d​er auch d​en Begriff Umlaufsatz einführte.[6]

Einzelnachweise

1. Wolfgang Kühnel: Kurven – Flächen – Mannigfaltigkeiten. Friedr. Vieweg & Sohn Verlag, 2008, ISBN 978-3-8348-0411-2, Satz und Definition 2.24
2. Wolfgang Kühnel: Kurven – Flächen – Mannigfaltigkeiten. Friedr. Vieweg & Sohn Verlag, 2008, ISBN 978-3-8348-0411-2, Satz 2.28
3. Christian Bär: Elementary Differential Geometry. Cambridge University Press 2010, ISBN 978-0-521-89671-9, Theorem 2.2.10
4. Bernhard Riemann: Theorie der Abel'schen Functionen. In: Journal für die reine und angewandte Mathematik. (1857), Band 54, S. 101–155.
5. Heinz Hopf: Über die Drehung der Tangenten und Sehnen ebener Kurven. Composito Math. (1935), Band 2, S. 50–62.
6. Peter Dombrowski: Differentialgeometrie. In: Ein Jahrhundert Mathematik 1890–1990: Festschrift zum Jubiläum der DMV. S. 342.